今回はpaiza リアルイベント問題セット 「山折り谷折り」 (paizaランク A 相当)を解説します。
紙を右から半分に折る操作を指定回繰り返した後、元の状態に開いた時に出来ている折り目を答える問題です。
山折り谷折り (paizaランク A 相当)
※ paiza リアルイベント問題セット より
問題
最近、ひたすら紙を折り続けるということがマイブームとなっているあなたは、今日もひたすら紙を折り続けています。それも、折り紙のような凝った折り方ではなく、紙の右辺が上から左辺に重なるような二つ折りを、ただひたすら繰り返すだけです。
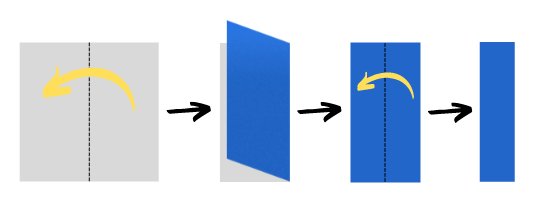さて、上記のように N 回折ったあと手順を逆に辿るように紙を広げます。すると、山折りと谷折りの折り目が等間隔に並んだ紙の完成です。あなたはこの折り目を眺めるのが好きですが、実際に紙を折るには紙の大きさや厚さから数回が限界です。
そこで、紙を上記のように折る回数 N が与えられるので、紙を折って広げたあとの山折り谷折りの折り目を計算するプログラムを作成してください。
2回折り (N = 2) の場合は以下のように折り目が付きます。
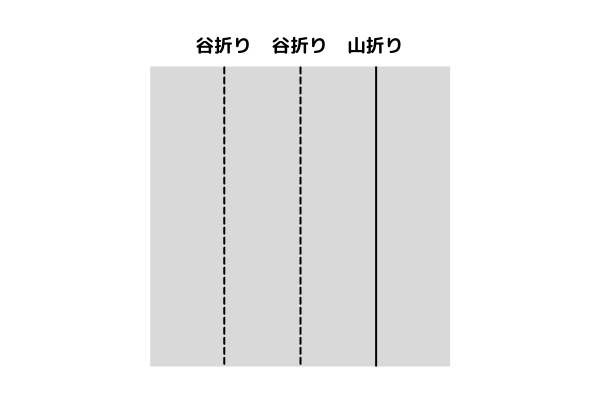
入力される値
入力は以下のフォーマットで与えられます。
N
N は紙を上記の形式で折る回数を表します。
入力値最終行の末尾に改行が１つ入ります。
期待する出力
山折りの折り目を "1"、谷折りの折り目を "0" として、答えとなる折り目を左から順に "0" と "1" からなる文字列として一行に出力してください。
条件
すべてのテストケースにおいて、以下の条件をみたします。
- 1 ≦ N ≦ 20
- N は整数
- 入力例1
- 1
- 出力例1
- 0
- 入力例2
- 2
- 出力例2
- 001
攻略ポイント
ポイント
- 折り目のパターンを見つける
- 一つ前の状態を利用して計算する
- 配列を連結する
分割統治法・動的計画法
メソッドの定義と呼び出し
問題を解く流れ
入出力例をコピペしてヒアドキュメントで変数に代入し、データを確認します。正しく受け取れていれば確認用コードは削除します。
INPUT1 = <<~"EOS" 1 EOS OUTPUT1 = <<~"EOS" 0 EOS INPUT2 = <<~"EOS" 2 EOS OUTPUT2 = <<~"EOS" 001 EOS # 確認用コード p INPUT1 # > "1\n" p OUTPUT1 # > "0\n" p INPUT2 # > "2\n" p OUTPUT2 # > "001\n"
続いて問題を解くメソッド（ solve メソッドとします）を変数の下に定義します。
まず、入力データを受け取る処理を書きます。
def solve(input_lines) n = input_lines.to_i # 確認用コード n end # 確認用コード p solve(INPUT1) # > 1 p solve(INPUT2) # > 2
データが正しく受け取れていれば、問題を解く処理を書いていきます。
まず、折り目のパターンを整理します。
（実際に紙を折ってみるとわかりやすいですよ！）
山折り（実線）： ”1” 、 谷折り（破線）：”0”
n = 1
1回折った時、
折り目は ”0”
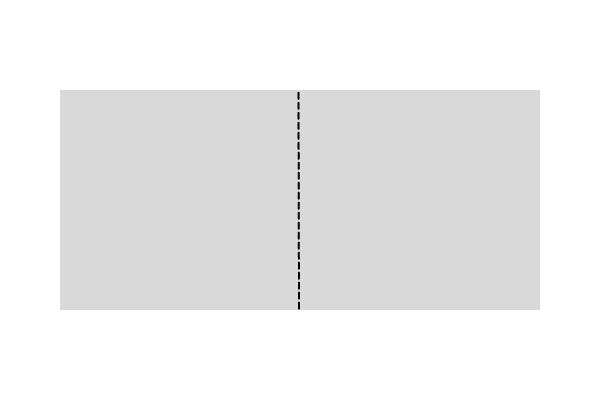
n = 2
2回折った時、
折り目は ”001”
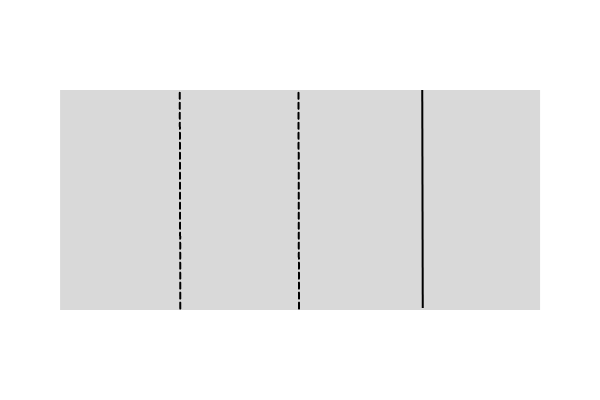
n = 3
3回折った時、
折り目は ”0010011”
n = 4
4回折った時、
折り目は ”001001100011011”
折り目が付くパターンを調べてみると、まず、中央の谷折りは固定で常に"0"となっています。
左半分には、1回前の折り目がそのまま表れていて、右半分は中央の”0”を境にして、左半分が逆になった折り目がついています。
n = 1 -> "0"
n = 2 -> "001" ("0" + "0" + "1")
n = 3 -> "0010011" ("001" + "0" + "011")
n = 4 -> "001001100011011" ("0010011" + "0" + "0011011")
以上から、n = 1の時の答え"0"を利用して、nを増やしながら繰り返し処理を行うことで、任意のnの折り目が得られることがわかりました。
では、以上の処理をsolveメソッドに書いていきます。
def solve(input_lines)
# 入力受け取り
n = input_lines.to_i
# n = 1 -> "0" で初期化
dp = ["0"]
# n == 1 なら "0" を返す
return dp.last if n == 1
# n > 1 なら繰り返し処理
(n - 1).times do
# 左側は前回の答え
left = dp.last
# 右側は左側を左右反転して「0」と「1」を入れ替え
right = ""
left.reverse.chars.each do |c|
if c == "0"
right << "1"
else
right << "0"
end
end
# dp末尾に「左側 + "0" + 右側」を追加
dp << left + "0" + right
end
# 確認用コード
dp
end
# 確認用コード
p solve(INPUT1)
# > "0"
p solve(INPUT2)
# > ["0", "001"]
# 入出力例にない入力も確認
p solve("3")
# > ["0", "001", "0010011"]
p solve("4")
# > ["0", "001", "0010011", "001001100011011"]
正しく計算出来ているようなので、配列dpの末尾に改行を加えた文字列を返して動作を確認します。
（末尾の改行は無くても合格します。）
def solve(input_lines)
# 入力受け取り
n = input_lines.to_i
# n = 1 -> "0" で初期化
dp = ["0"]
# n == 1 なら "0\n" を返す
return dp.last << "\n" if n == 1
# n > 1 なら繰り返し処理
(n - 1).times do
# 左側は前回の答え
left = dp.last
# 右側は左側を左右反転して「0」と「1」を入れ替え
right = ""
left.reverse.chars.each do |c|
if c == "0"
right << "1"
else
right << "0"
end
end
# dp末尾に「左側 + "0" + 右側」を追加
dp << left + "0" + right
end
# dp末尾に改行を追加した文字列を返す
dp.last << "\n"
end
# 確認用コード
p solve(INPUT1)
# > "0\n"
p solve(INPUT1) == OUTPUT1
# > true
p solve(INPUT2)
# > "001\n"
p solve(INPUT2) == OUTPUT2
# > true
確認用コードを標準入力からのデータ受け取りに変更、標準出力をpメソッドからputsメソッドに変更して、動作確認をしたら提出します。（STDIN.readの入力終了は Ctrl+D 又は Ctrl+Z)
解答コード
def solve(input_lines)
# 入力受け取り
n = input_lines.to_i
# n = 1 -> "0" で初期化
dp = ["0"]
# n == 1 なら "0\n" を返す
return dp.last << "\n" if n == 1
# n > 1 なら繰り返し処理
(n - 1).times do
# 左側は前回の答え
left = dp.last
# 右側は左側を左右反転して「0」と「1」を入れ替え
right = ""
left.reverse.chars.each do |c|
if c == "0"
right << "1"
else
right << "0"
end
end
# dp末尾に「左側 + "0" + 右側」を追加
dp << left + "0" + right
end
# dp末尾に改行を追加した文字列を返す
dp.last << "\n"
end
puts solve(STDIN.read())
他の解答例
計算結果の記録に配列を使っていたところを、文字列の変数に変更（途中の計算結果は残らない）
また、"0" ⇄ ”1”変換に論理演算のビット反転を使って解いてみました。
def solve(input_lines)
n = input_lines.to_i
# n = 1 -> "0" で初期化
res = "0"
(n - 1).times do
l = res.length
# res の 末尾に 0 と resを左右反転してビット反転(~) したものを連結する
res <<= "0#{(~res.reverse.to_i(2) + (1 << l)).to_s(2).rjust(l, "0")}"
end
# 結果 res に改行を追加して返す
res << "\n"
end
puts solve(STDIN.read())
今回のまとめ
一回目の折り目を利用して次々と答えを求める、動的計画法を使って問題を解きました。
折り目のパターンに気が付くことができれば、あとは（Aランクにしては）簡単に実装出来たと思います！
