こんにちは!じゃいごテックのあつしです。
今回はデータ構造の基本、スタックやキュー、木構造についてご紹介します。また、優先度付きキューの仕組みについても解説したいと思います。
スタック
スタック(stack) は、データが入ってきた順に並べて後に入れたデータから順番に取り出す規則で作られたデータ構造で、後に入れたものを先に出すので後入れ先出し ( LIFO: Last In First Out ) と呼ばれます。
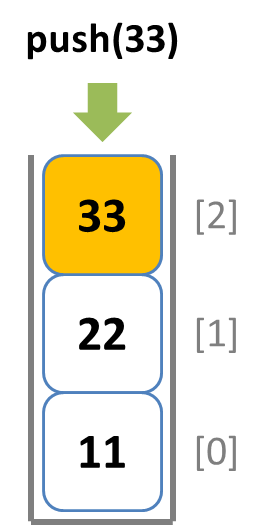
スタックにデータを入れることをプッシュ(push) 、データを取りだすことをポップ(pop)といいます。
1冊ずつ本を積んで行って、上から読んでいくイメージです。
スタックのサンプルコード
Rubyでは配列に対して push -> pushメソッドと pop -> popメソッドでスタックを実装することが出来ます。
stack = [] stack.push(11) stack.push(22) stack.push(33) p stack # > [11, 22, 33] p stack.pop # > 33 p stack.pop # > 22 p stack.pop # > 11
- pushメソッドで配列末尾から 11, 22, 33 を順番に挿入します。
- popメソッドで配列末尾から要素を順番に取り出します。
push: pushメソッドで末尾側から要素を挿入する
pop: popメソッドで末尾側から要素を取り出す
キュー
キュー(queue) は、データが入ってきた順に並べて先に入れたデータから順番に取り出す規則で作られたデータ構造です。
先に入れたものから先に出すので先入れ先出し( FIFO: First In First Out )と呼ばれます。
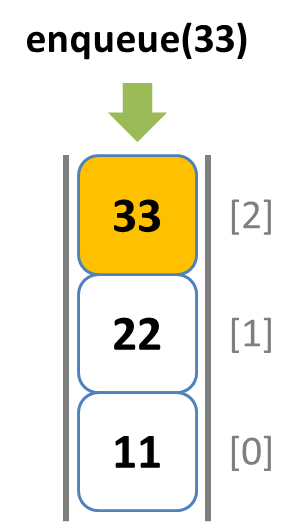
キューにデータを入れることをエンキュー(enqueue)、データを取りだすことをデキュー(dequeue)といいます。
身近な例でいうとプリンタの印刷待ちや、レジの順番待ちです。
キューのサンプルコード
Rubyでは配列に対して enqueue -> pushメソッドと dequeue -> shiftメソッドでキューを実装することが出来ます。
queue = [] queue.push(11) queue.push(22) queue.push(33) p queue # > [11, 22, 33] p queue.shift # > 11 p queue.shift # > 22 p queue.shift # > 33
- pushメソッドで配列末尾から 11, 22, 33 を順番に挿入します。
- shiftメソッドで配列先頭から要素を順番に取り出します。
enqueue: pushメソッドで末尾側から要素を挿入する
dequeue: shiftメソッドで末尾側から要素を取り出す
両端キュー
両端キュー(double-ended queue または deque) は、データ列の先頭・末尾のどちらからでもデータを追加・取り出しできるデータ構造です。
ビーズアクセサリを作るイメージです。
両端キューのサンプルコード
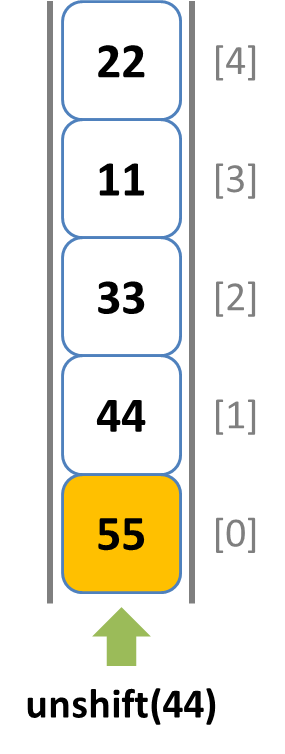
Rubyでは配列に対して 先頭へ追加 -> unshiftメソッド、先頭から取り出し -> shiftメソッド、末尾への追加 -> pushメソッド、末尾から取り出し -> popメソッドで実装することが出来ます。
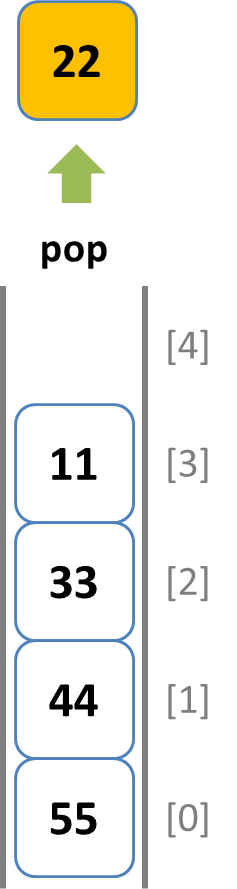
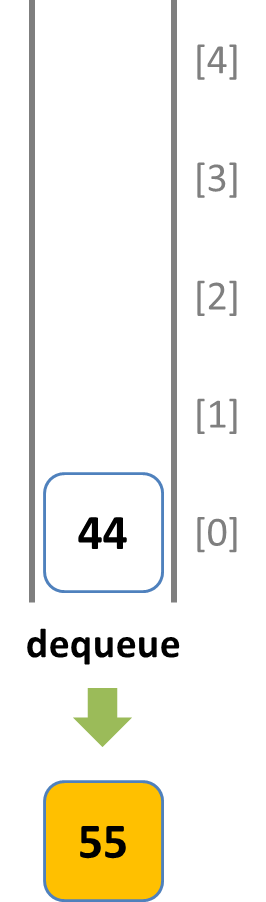
deque = [] deque.push(11) deque.push(22) deque.unshift(33) deque.unshift(44) deque.unshift(55) p deque # > [55, 44, 33, 11, 22] p deque.pop # > 22 p deque.pop # > 11 p deque.pop # > 33 p deque.shift # > 55 p deque.shift # > 44
- pushメソッドで配列末尾から 11, 22 を順番に挿入します。
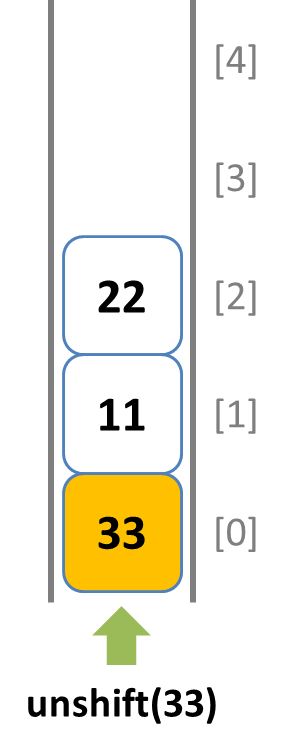
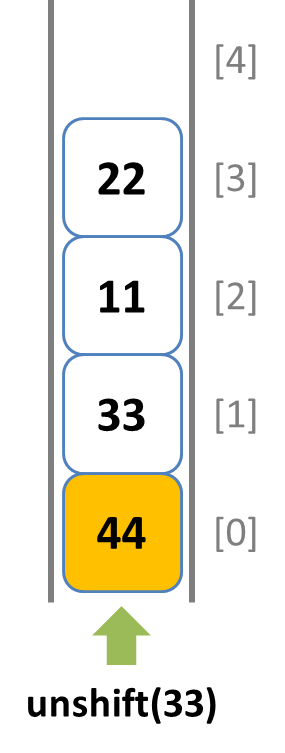
- ubshiftメソッドで配列先頭から 33, 44, 55 を順番に挿入します。
- popメソッドで配列末尾から3個の要素を順番に取り出します。
- shiftメソッドで配列先頭から2個の要素を順番に取り出します。
pushメソッドで末尾側から要素を挿入する
unshiftメソッドで先頭側から要素を挿入する
popメソッドで末尾側から要素を取り出す
shiftメソッドで先頭側から要素を取り出す
木構造
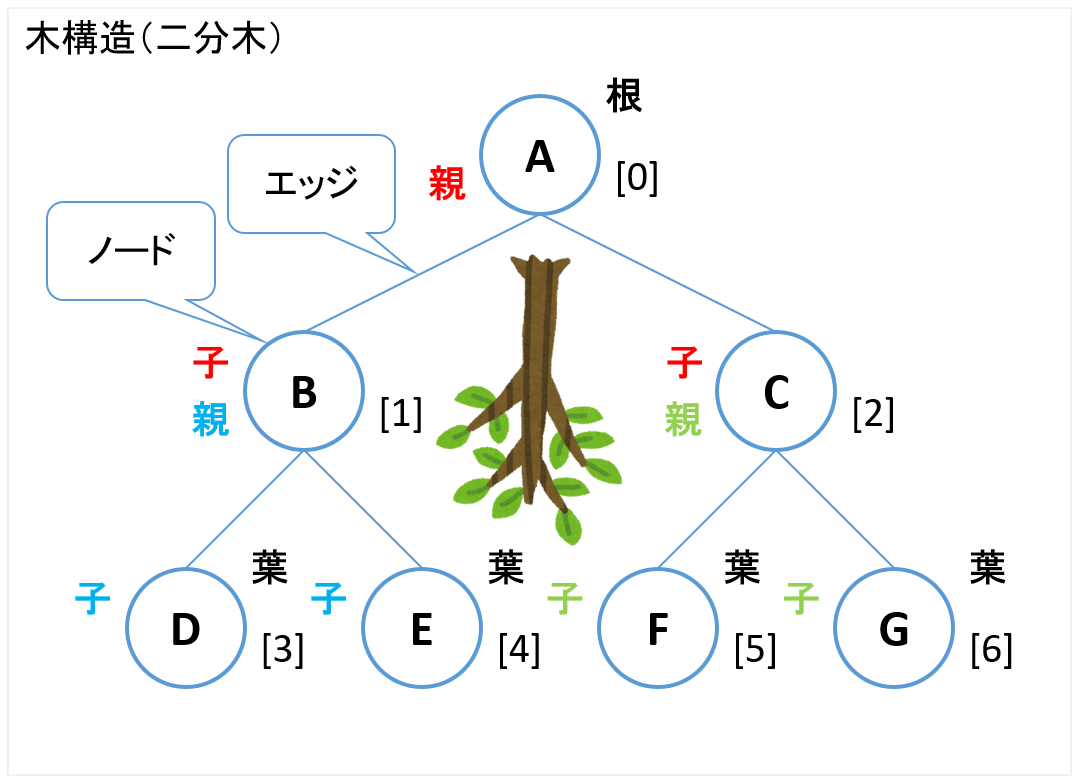
木構造とは、1つの要素が複数の子要素をもち、さらに子要素が複数の孫要素をもつような形で、下位層が深くなるほど枝分かれしていくデータ構造のことです。
ノード(node) : 節(枝がわかれるところ)です。
根ノード(root node) : 親を持たないノード、頂点ノードです。
葉ノード(leaf node) : 子を持たないノード、末端ノードです。
エッジ(edge) : ノードとノードを結ぶリンクです。
二分木(binary tree) : 子の数が2個以下になっている木構造です。
ヒープ(heap) : 木構造のうち、親要素が常に子要素より大きい(又は小さい)という条件を満たす構造です。
二分ヒープ(binary heap) : 二分木とヒープの条件を満たした構造です。
優先度付きキュー
データを優先度付きで追加し、優先度が高いものから取り出すデータ構造です。
優先度の異なるタスクが沢山あって、処理中にも新しいタスクが入ってるが、常に優先度の高いものから処理するようなイメージです。
優先度付きキューサンプルコード
※ Aizu Online Judgeで優先度付きキューを実装する課題 AOJ ALDS1_9_C がありますので、同じ仕様で実装してみます。
class PriorityQueue
def initialize
@data = []
end
# 要素追加
def insert(element)
@data.push(element)
up_heap
end
# 要素取り出し
def extract
return @data.pop if @data.length <= 1
target_element = @data[0]
@data[0] = @data.pop
down_heap
target_element
end
private
# ノード交換
def swap(a, b)
@data[a], @data[b] = @data[b], @data[a]
end
# 親 index
def parent_idx(idx)
idx / 2 + idx % 2 - 1
end
# 左の子 index
def left_child_idx(idx)
(idx * 2) + 1
end
# 右の子 index
def right_child_idx(idx)
(idx * 2) + 2
end
# 子が存在するか?
def has_child?(idx)
((idx * 2) + 1) < @data.size
end
# 葉から根方向 ノード比較・交換
def up_heap
idx = @data.length - 1
return if idx == 0
parent_idx = parent_idx(idx)
while (@data[parent_idx] < @data[idx])
swap(parent_idx, idx)
return if parent_idx == 0
idx = parent_idx
parent_idx = parent_idx(idx)
end
end
# 根から葉方向 ノード比較・交換
def down_heap
idx = 0
while (has_child?(idx))
l_idx = left_child_idx(idx)
r_idx = right_child_idx(idx)
if @data[r_idx].nil?
target_idx = l_idx
else
target_idx = @data[l_idx] >= @data[r_idx] ? l_idx : r_idx
end
if @data[idx] < @data[target_idx]
swap(idx, target_idx)
idx = target_idx
else
return
end
end
end
end
pqueue = PriorityQueue.new
pqueue.insert(33)
pqueue.insert(11)
pqueue.insert(22)
pqueue.insert(55)
pqueue.insert(44)
pqueue.insert(66)
p pqueue
# > <PriorityQueue:0x00007fffe5d2cb38 @data=[66, 44, 55, 11, 33, 22]>
p pqueue.extract
# > 66
p pqueue.extract
# > 55
p pqueue.extract
# > 44
p pqueue.extract
# > 33
p pqueue.extract
# > 22
p pqueue.extract
# > 11

insert(33)
- ノードを追加します。
- 最初のノードなので比較・交換はありません。
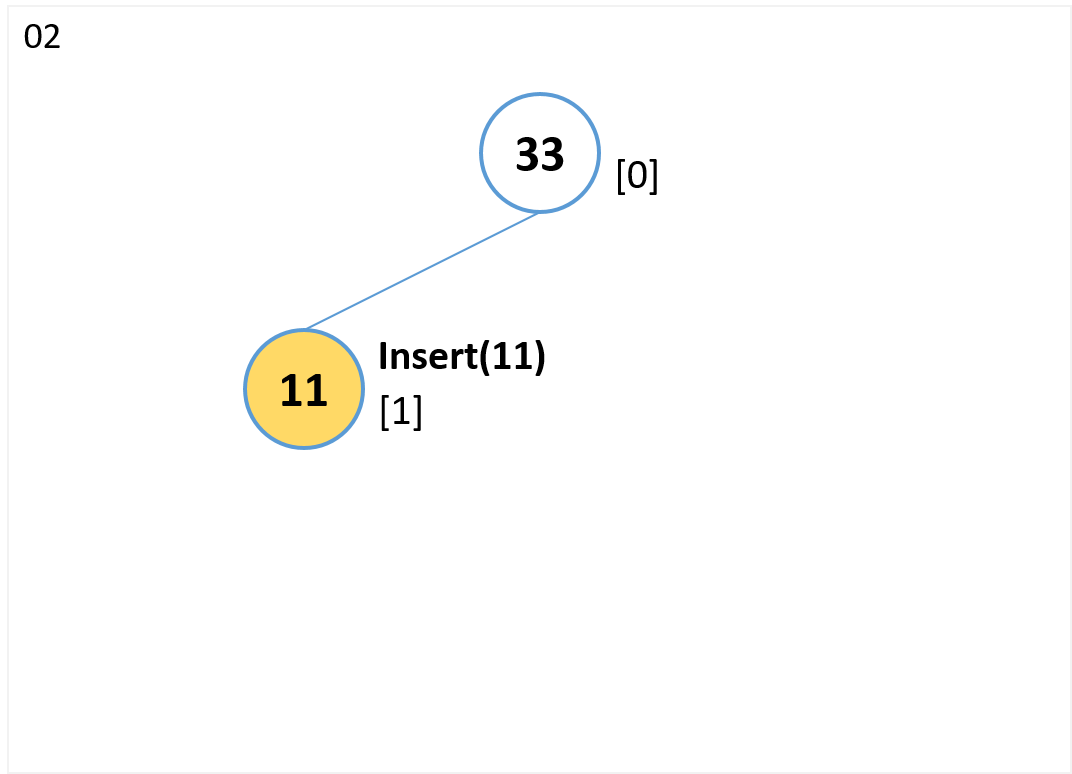
insert(11)
- 末尾[1] にノードを追加します。
(ノード[0]の左の子ノードになる) - 親(ノード[0])より値が小さいのでノード交換はありません。
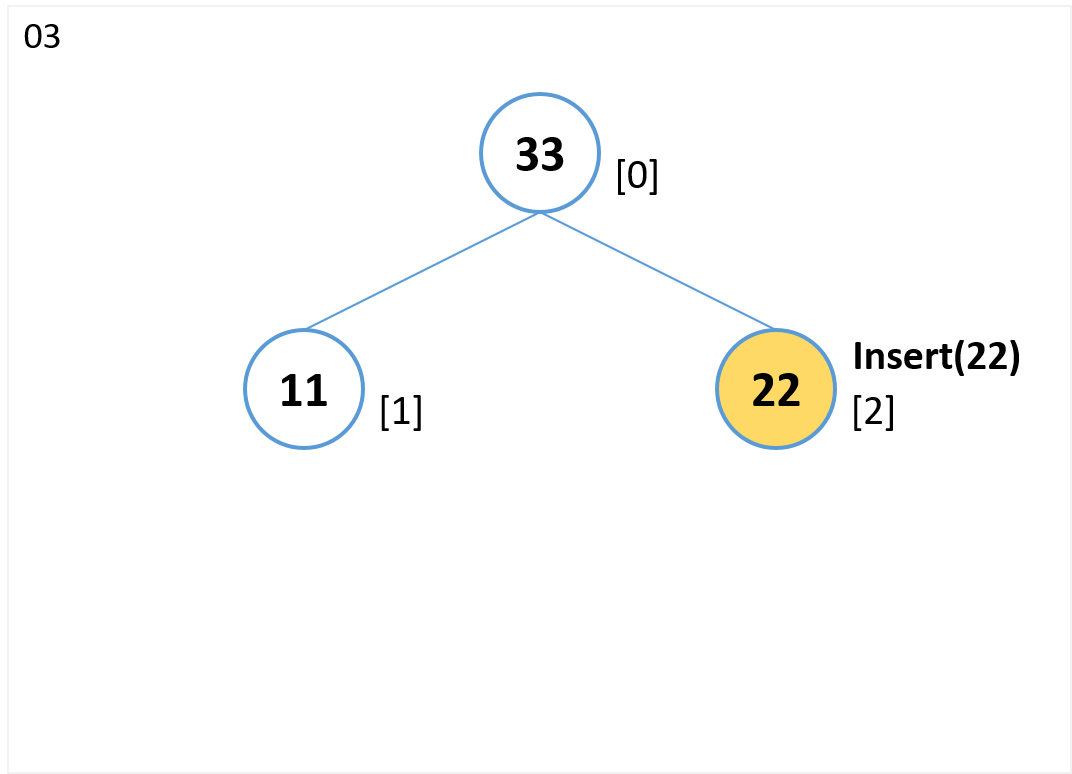
insert(22)
- 末尾[2] にノードを追加します。
(ノード[0]の右の子ノードになる) - 親(ノード[0])より値が小さいのでノード交換はありません。
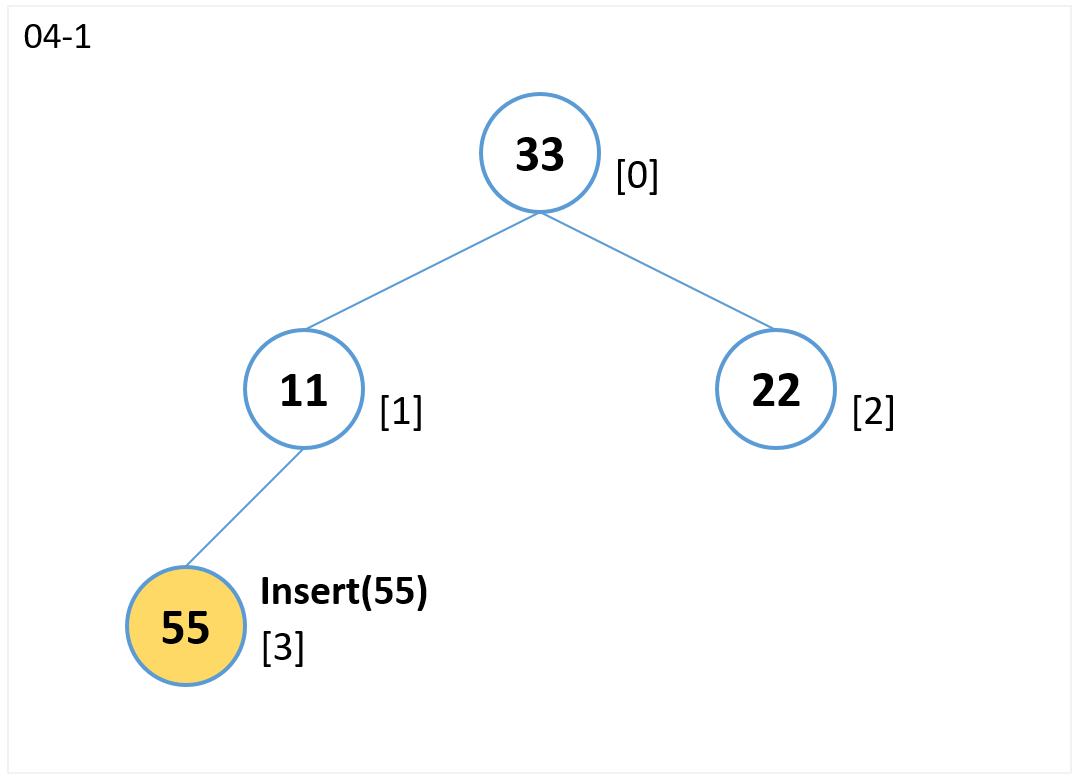
insert(55)
- 末尾[3] にノードを追加します。
(ノード[1]の左の子ノードになる)
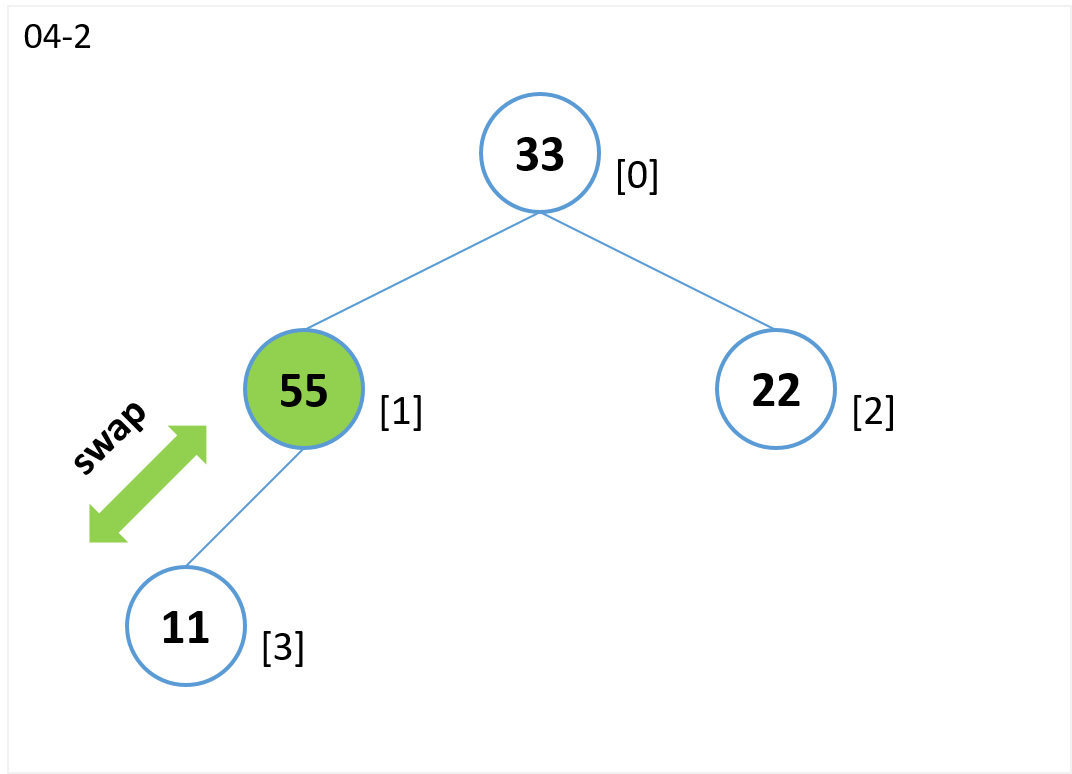
- ノード[3](子)とノード[1](親)を比較します。
- ノード[3](子)がノード[1](親)より値が大きいのでノード[3]とノード[1]を交換します。
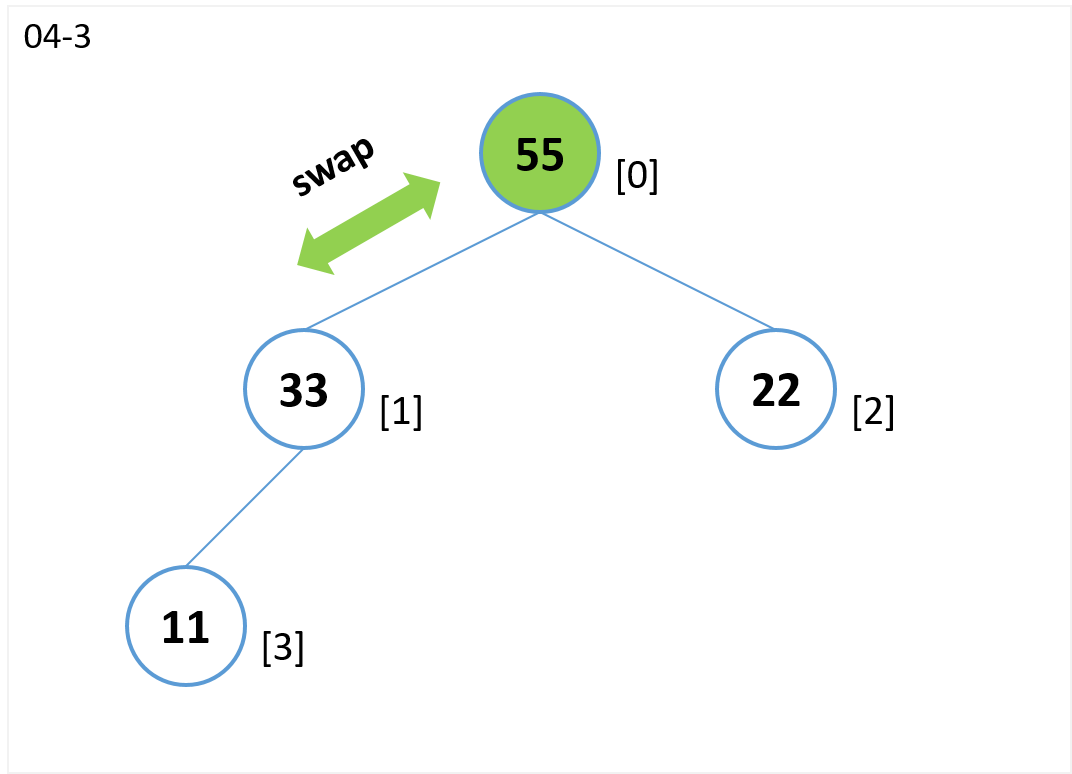
- ノード[1](子)とノード[0] (親)を比較します。
- ノード[1](子)がノード[0](親)より値が大きいのでノード[1]とノード[0]を交換します。
- 根(ノード[0])まで比較したので終了。
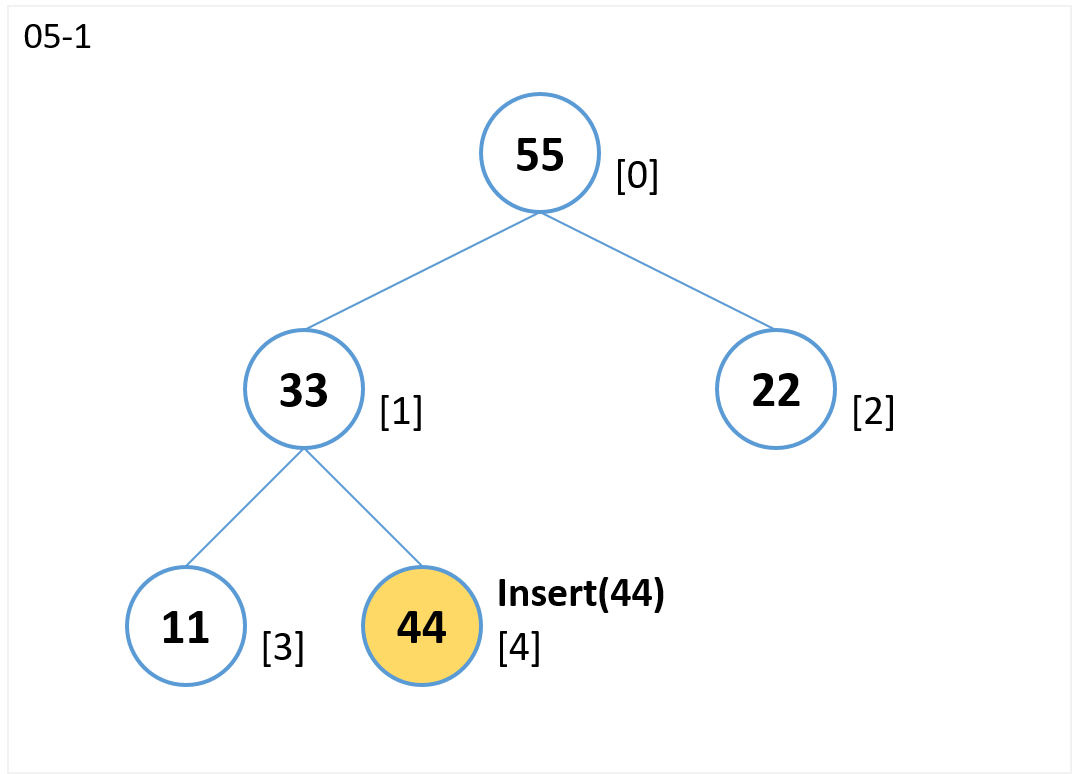
insert(44)
- 末尾[4] にノードを追加します。
(ノード[1]の右の子ノードになる)
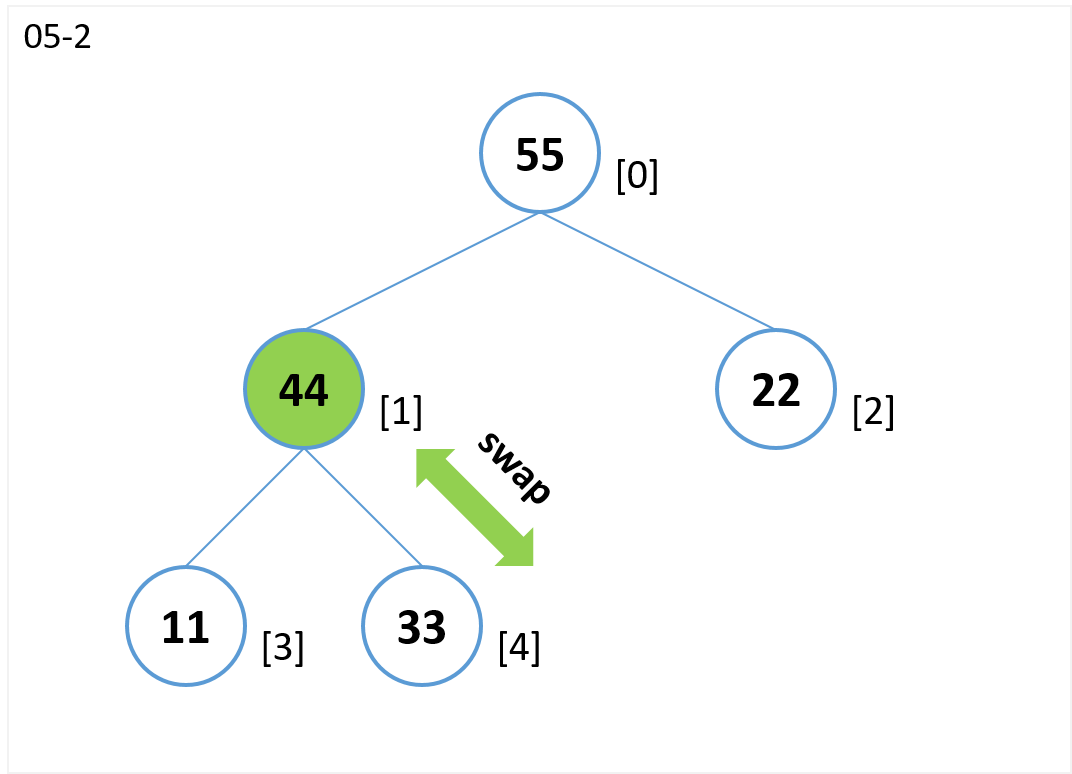
- ノード[4](子)とノード[1](親)を比較します。
- ノード[4](子)がノード[1](親)より値が大きいのでノード[4]とノード[1]を交換します。
- ノード[1](子)とノード[0](親)を比較します。
- ノード[1](子)はノード[0](親)より値が小さいので比較終了
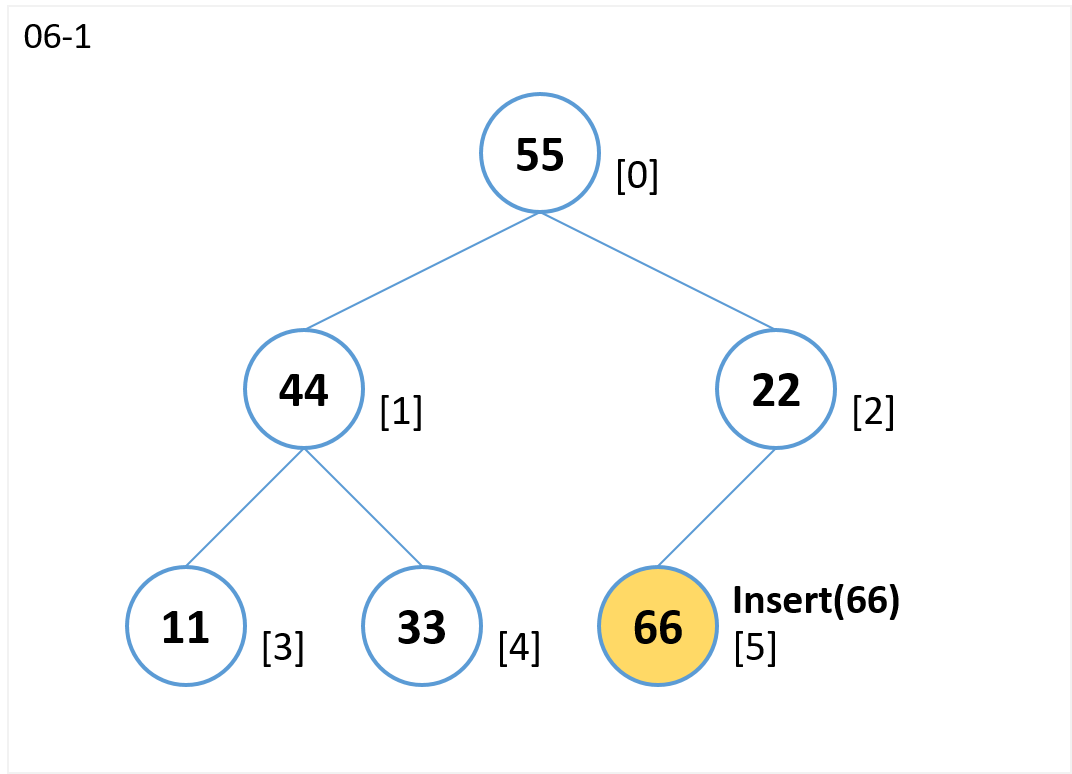
insert(66)
- 末尾[5] にノードを追加します。
(ノード[2]の右の子ノードになる)
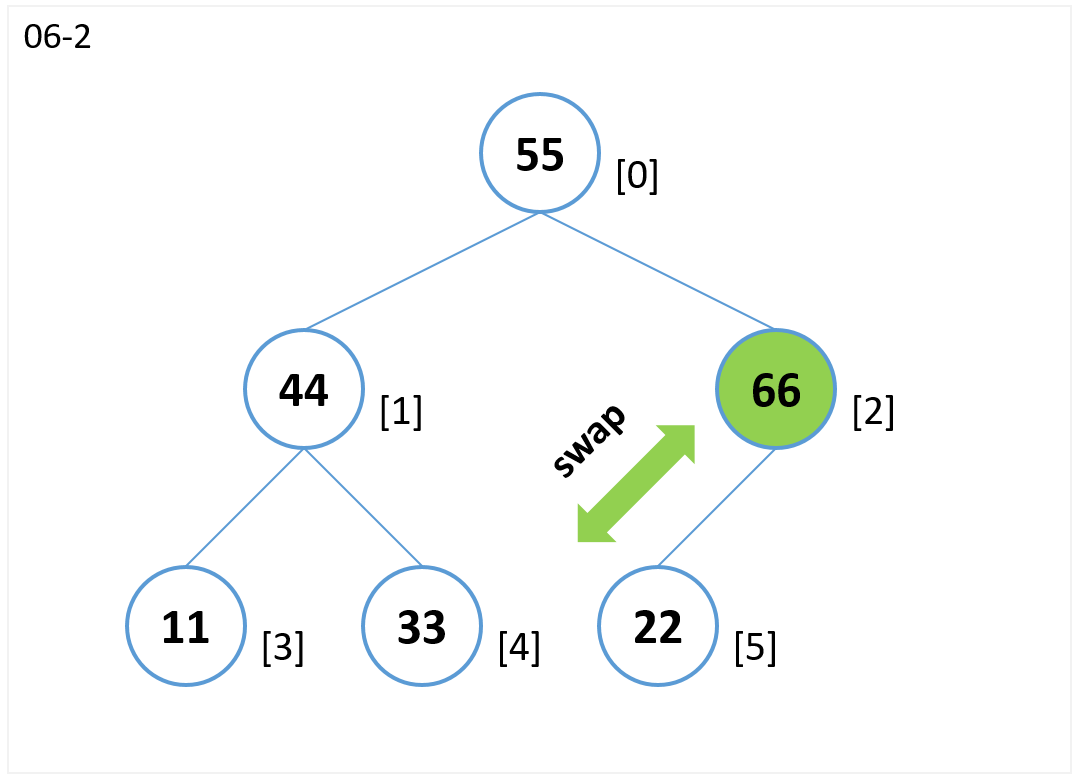
- ノード[5](子)とノード[2](親)を比較します。
- ノード[5](子)がノード[2](親)より値が大きいのでノード[5]とノード[2]を交換します。
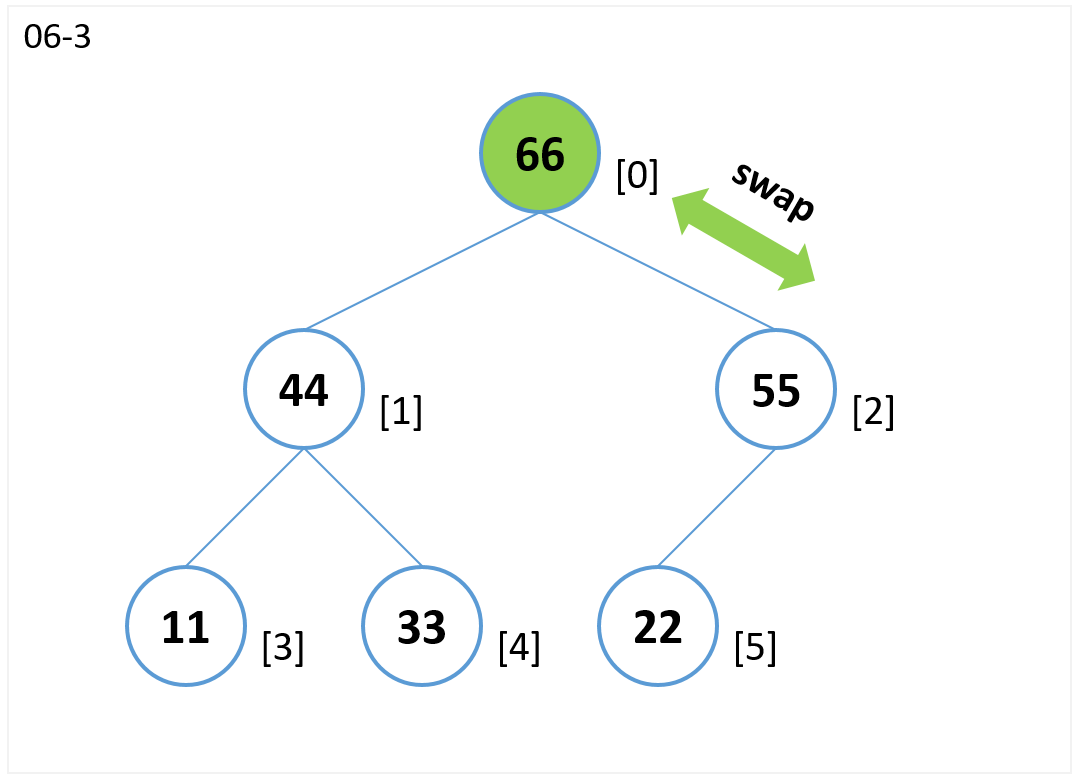
- ノード[2](子)とノード[0] (親)を比較します。
- ノード[2](子)がノード[0](親)より値が大きいのでノード[2]とノード[0]を交換します。
- 根(ノード[0])まで比較したので終了。
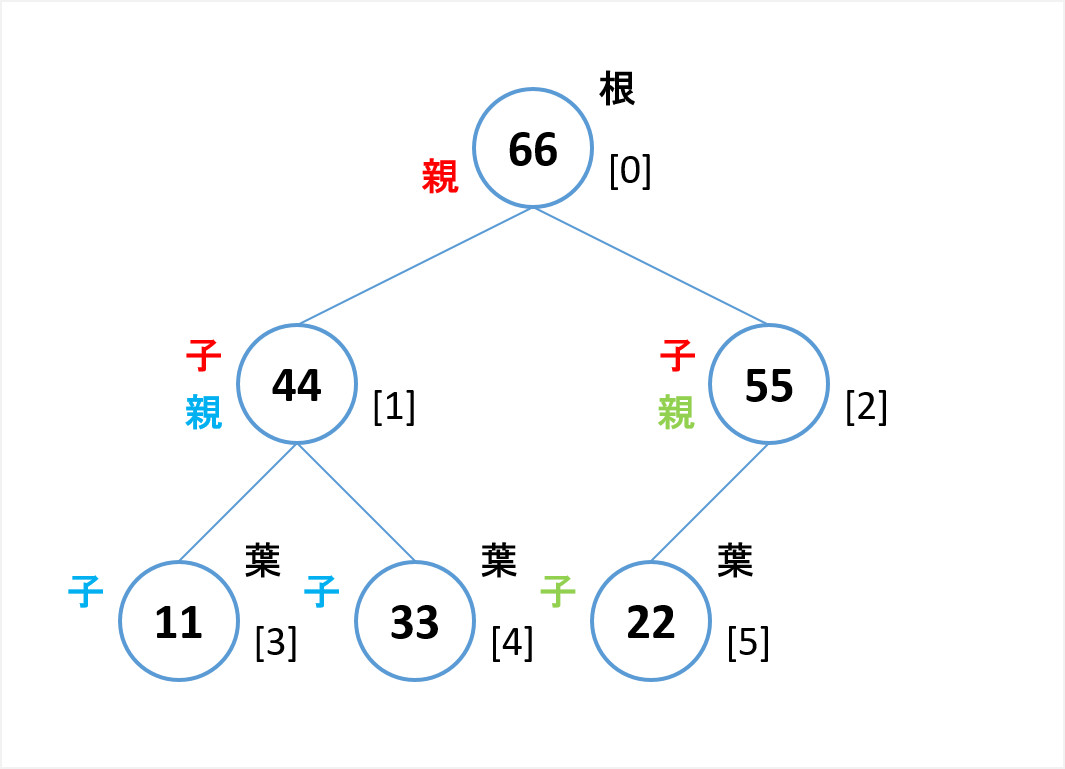
挿入が完了した状態
二分木かつヒープなので、二分ヒープ構造(Binary heap)となっています。
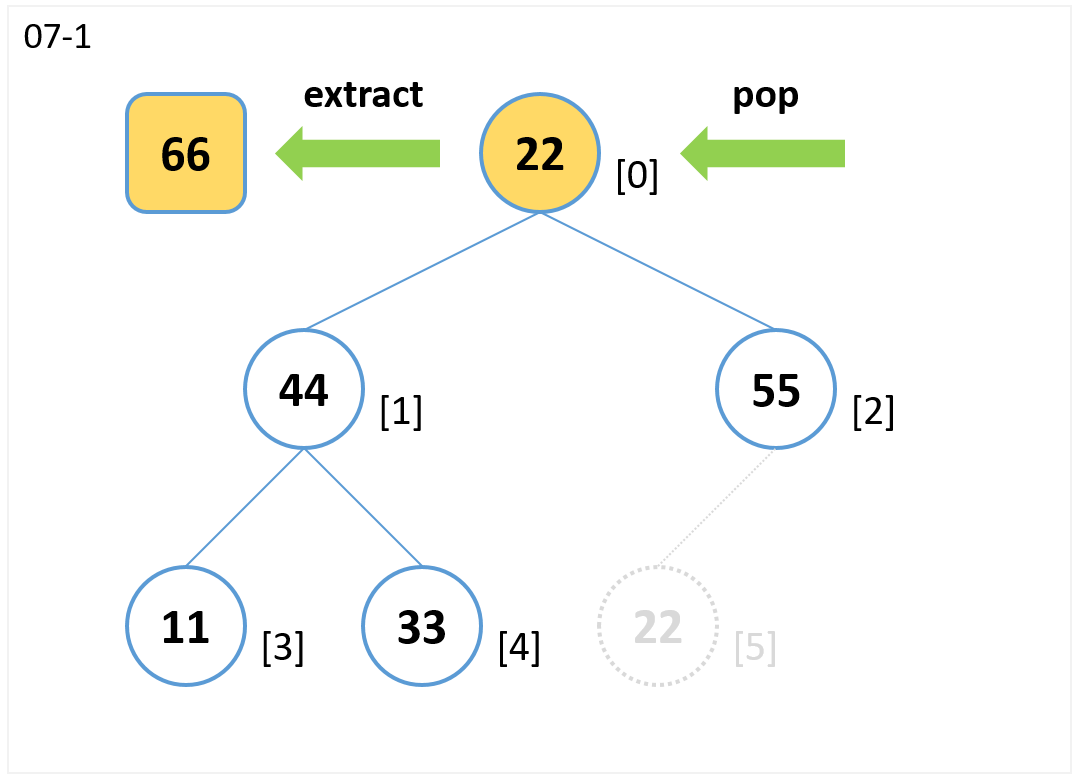
extract
- 根ノードを参照して値 (66) を取り出します。
- 末尾ノード[5] を pop で取り出し、根ノードを上書きします。
- 子のノードのうち値が大きいノード[2] と 比較します。
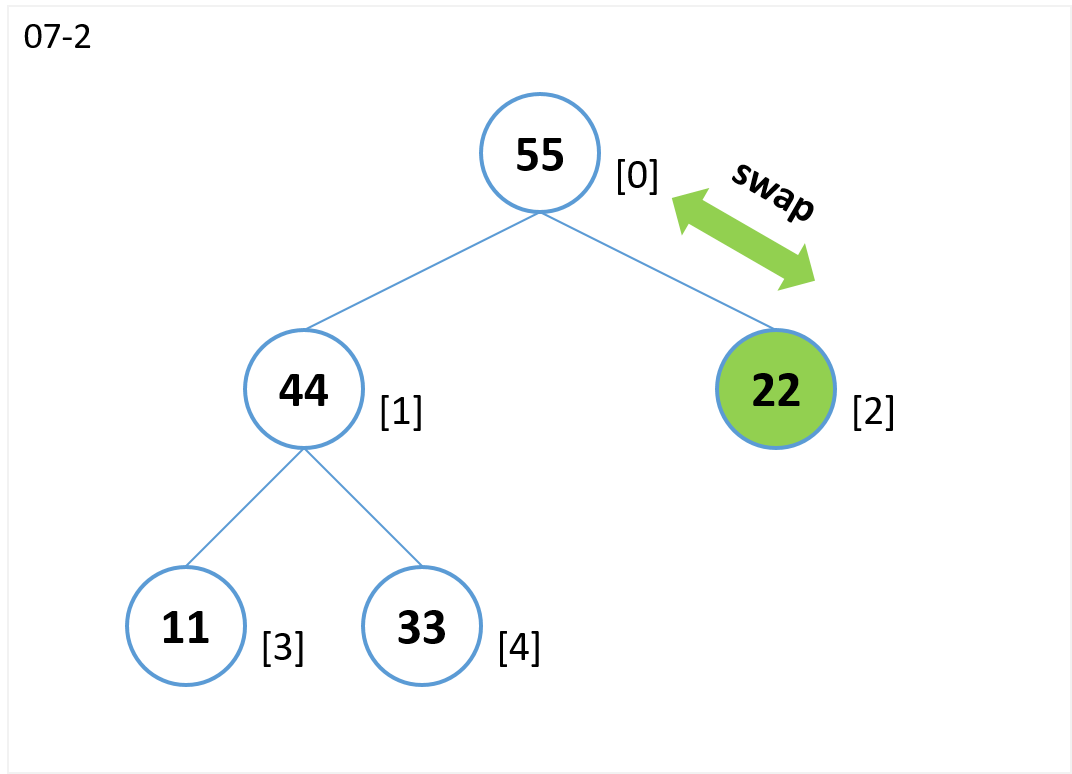
- ノード[0](親)よりノード[2](子)が値が大きいのでノード[0]とノード[2]を交換します。
- 葉(ノード[2])まで比較したので終了。
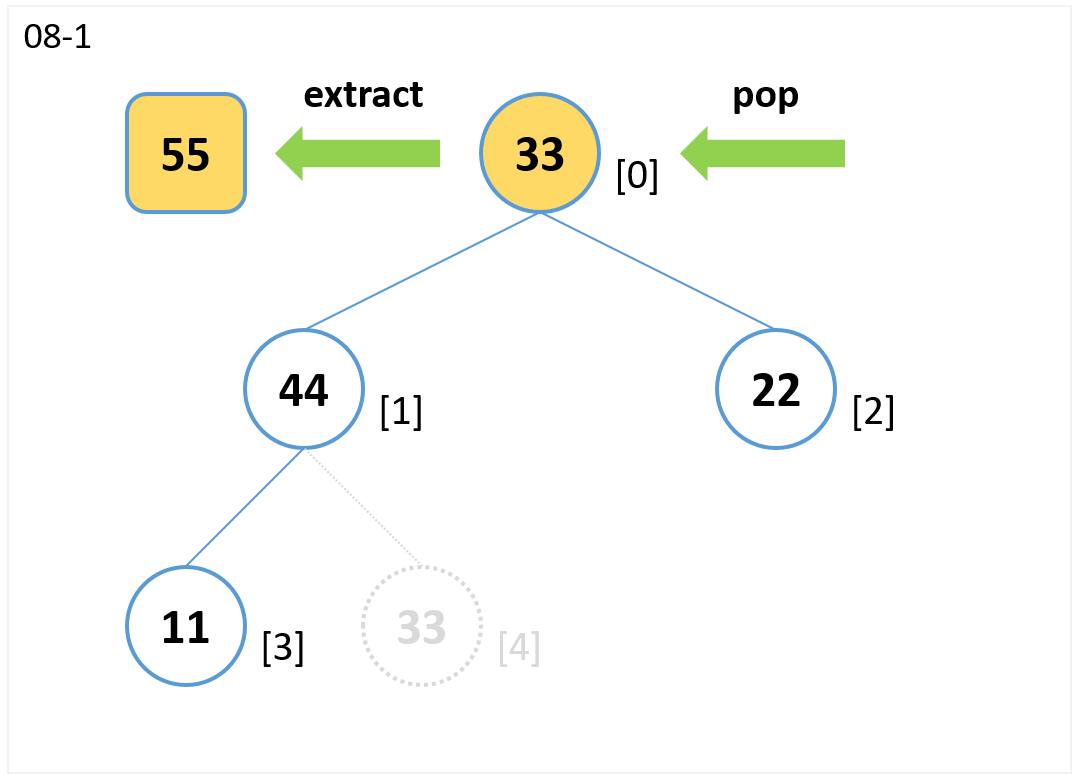
extract
- 根ノードを参照して値 (55) を取り出します。
- 末尾ノード[4]をpopで取り出し、根ノードを上書きします。
- 子のノードのうち値が大きいノード[1] と比較します。
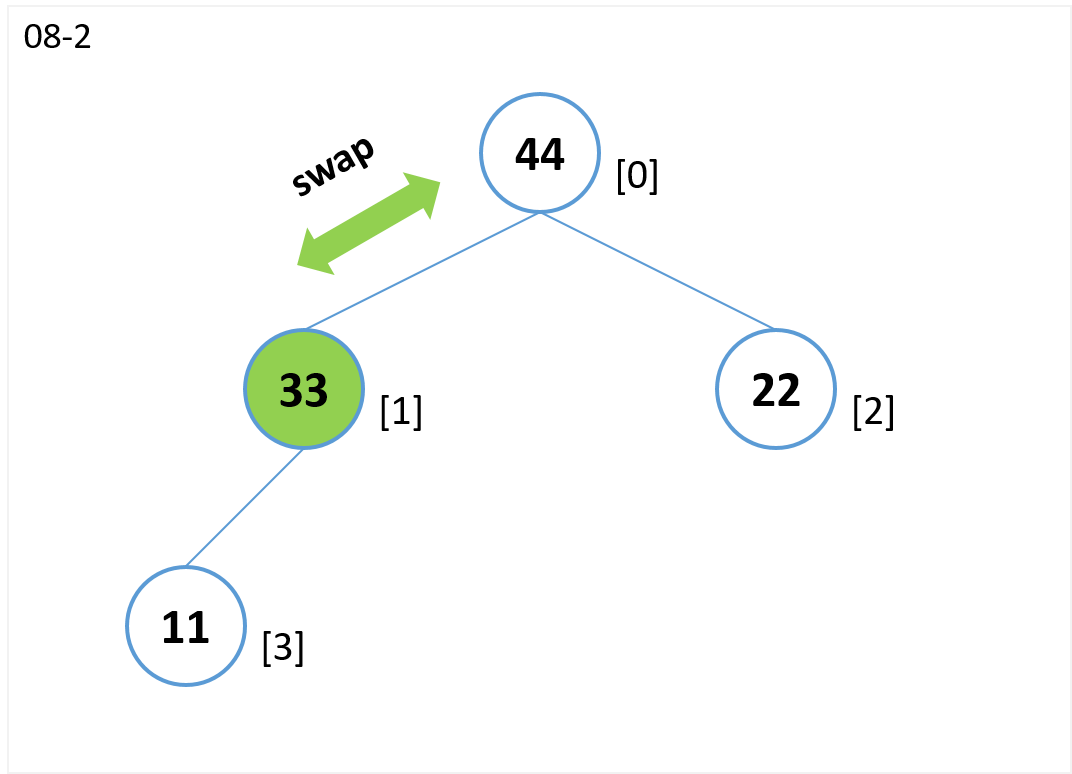
- ノード[0](親)よりノード[1](子)が値が大きいのでノード[0]とノード[1]を交換します。
- ノード[1](親)とノード[3](左の子)を比較すると、親の方が大きいので終了。
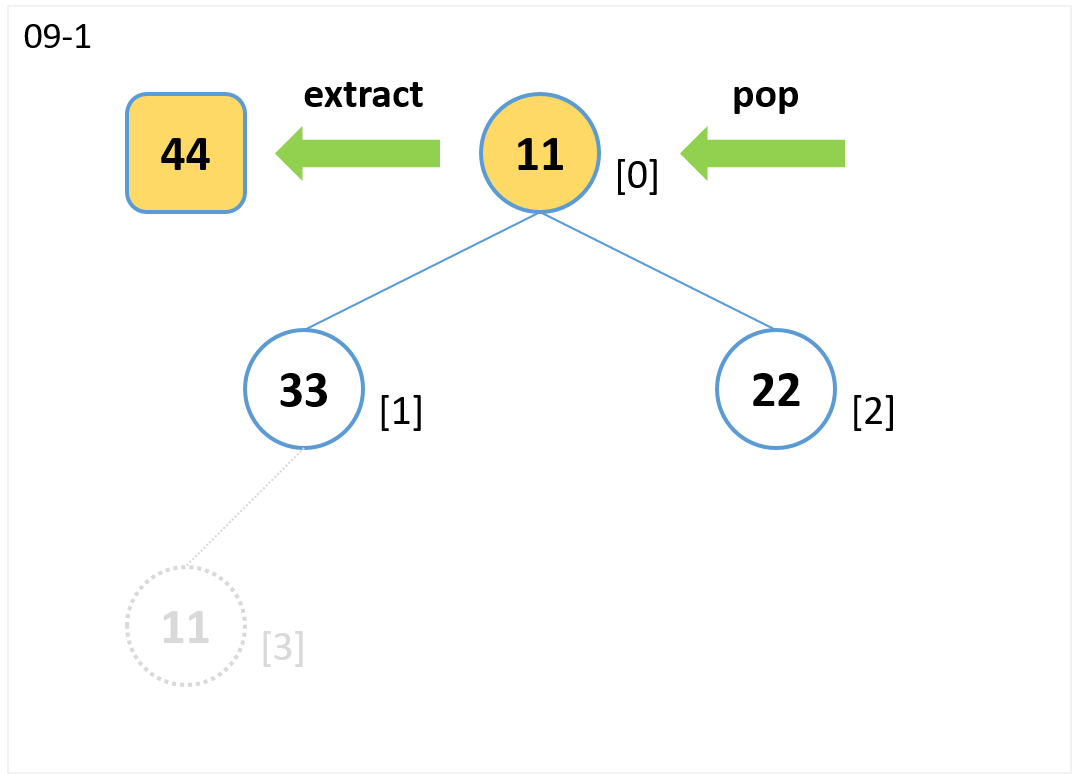
extract
- 根ノードを参照して値 (44) を取り出します。
- 末尾ノード[3]をpopで取り出し、根ノードを上書きします。
- 子のノードのうち値が大きいノード[1] と 比較します。
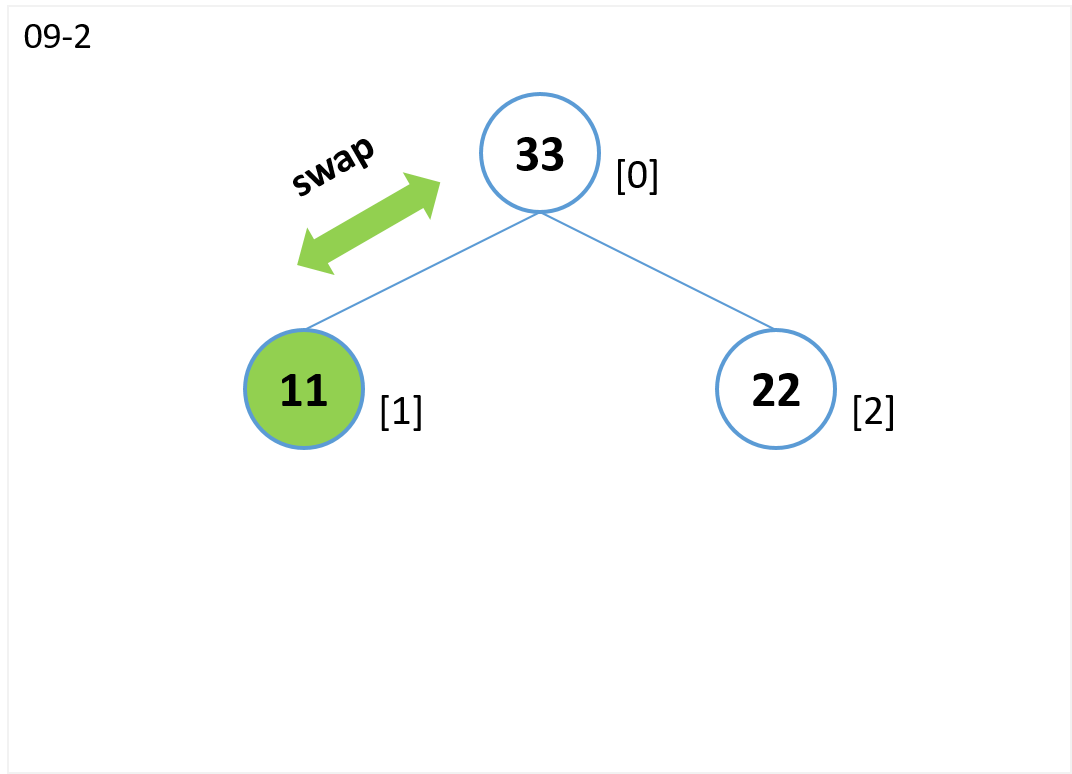
- ノード[0](親)よりノード[1](子)が値が大きいのでノード[0]とノード[1]を交換します。
- 葉(ノード[1])まで比較したので終了。
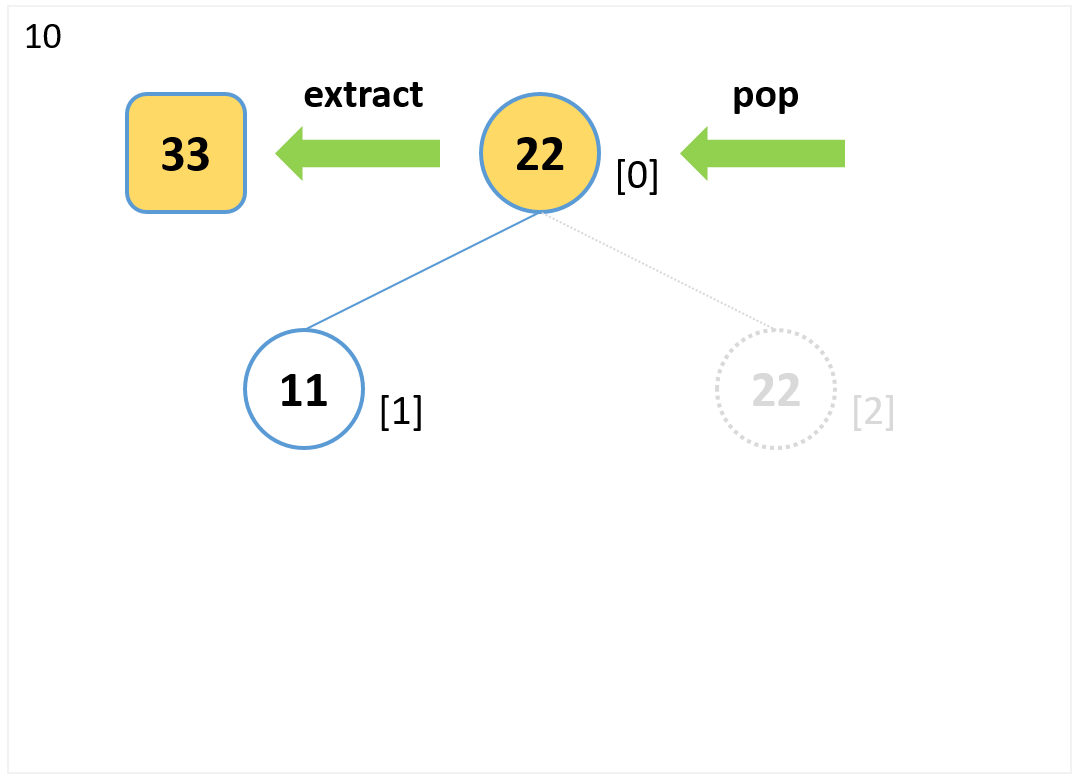
extract
- 根ノードを参照して値 (33) を取り出します。
- 末尾ノード[2]をpopで取り出し、根ノードを上書きします。
- ノード[0](親)がノード[1](子)よりが値が大きいので終了
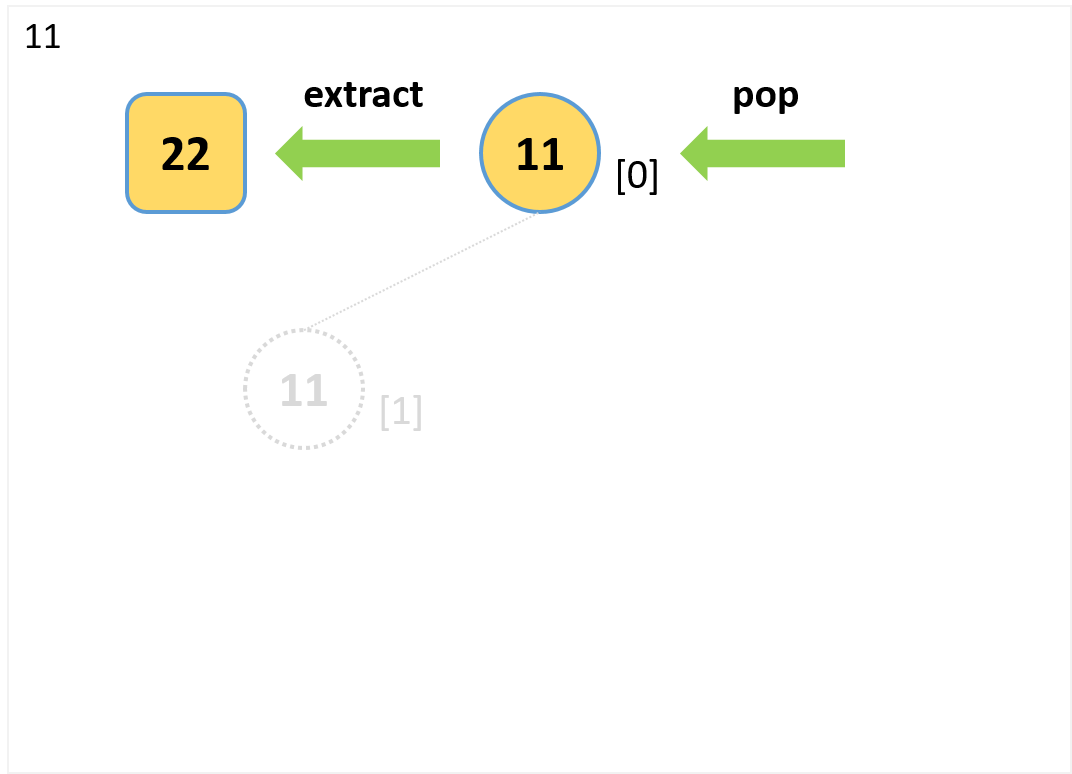
extract
- 根ノードを参照して値 (22) を取り出します。
- 末尾ノード[2]をpopで取り出し、根ノードを上書きします。
- 子ノードがないので比較はありません。
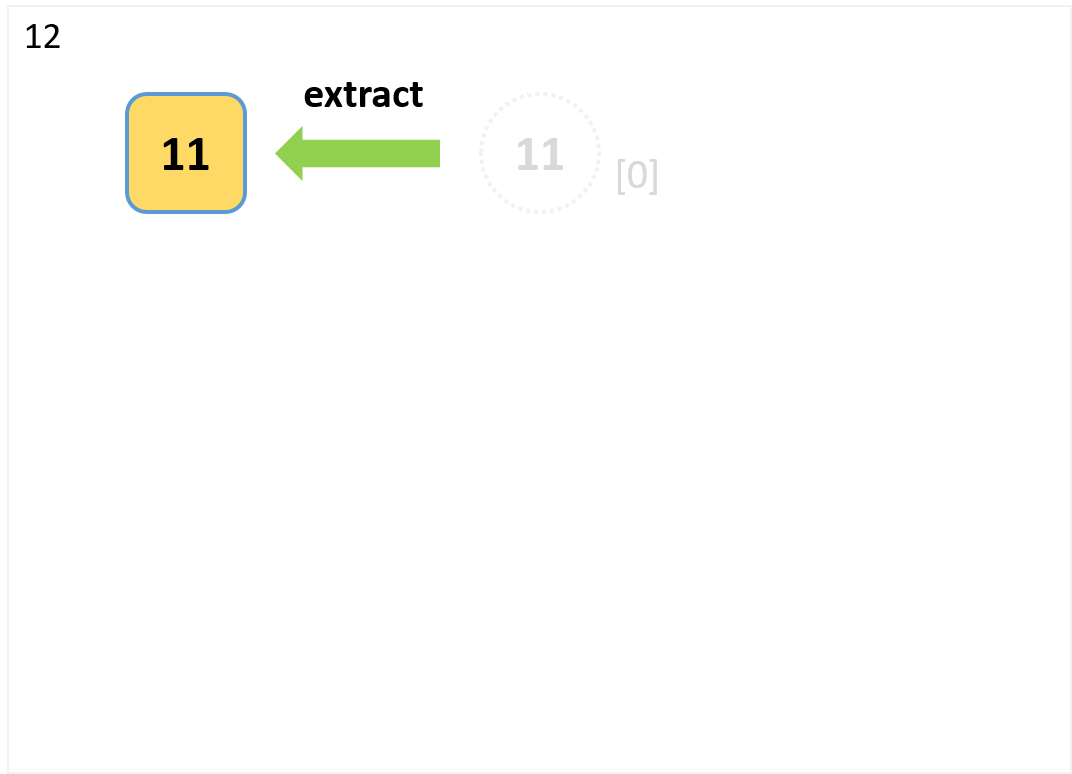
extract
- 要素数1なのでpopで取り出して終了
今回のまとめ
スタックは深さ優先探索(depth-first search: DFS)、キューは幅優先探索(breadth first search: BFS)に使われます。また、両端キューや木構造もアルゴリズムを実装するときに便利です。プログラミング言語によっては標準ライブラリに含まれていますので調べて使ってみて下さい!

データ構造を理解すると、アルゴリズムを考えるときに良いアイデアが浮かんだりしますのでじっくり取り組んでみて下さい!