こんにちは!じゃいごテックのあつしです。
今回は複雑な問題を解く際に用いられるアルゴリズム、分割統治法(divide and conquer)と、動的計画法(dynamic programming)をご紹介します。
どちらも大きな問題を複数の小さな問題に分けて解いていく手法です。
分割統治法(divide and conquer)
そのままでは解決できない大きな問題を小さな問題に分割し、そのすべてを解決することで、最終的に最初の問題全体を解決する、という問題解決の手法です。(引用: Wikipedia 分割統治法)
マージソート
分割統治法を使った例として、マージソート(merge sort)が有名なのでサンプルコードと図を使って解説します。
マージソートは、挿入ソートやバブルソートの計算量O(n2)に対し、計算量がO(n log n)の比較的早いソートアルゴリズムです。
処理の流れ(全体)
- 中央から左右に2分割して、先頭から中央までの配列(左側)と中央から末尾の配列(右側)に分ける
- 左側の配列、右側の配列の要素数が2以上なら、その配列を引数に与えて再起呼び出し(メソッドの中で自分自身を呼び出す)を行う
- 要素数が1まで分割されると、その要素が返る
呼び出し元の左側配列ならary_l、呼び出し元の右側配列ならary_rに代入する - 返ってきた配列
ary_l, ary_rを昇順に並び替えながら併合(マージ)していく- 空の配列を用意する (
sorted_aryとする) ary_lとary_rが空になるまで繰り返すary_lとary_rのどちらかが空なら要素がある方の先頭の値をsorted_aryの末尾に追加するary_lとary_rの先頭を比べて値が小さい方を取り出してsorted_aryの末尾に追加する
sorted_aryを返す
- 空の配列を用意する (
サンプルコード
def merge_sort(ary)
# 要素が 1 個になるまで分割する
al = ary.length
return ary if al == 1
mid = al / 2
ary_l = merge_sort(ary[..mid - 1])
ary_r = merge_sort(ary[mid..])
# 分割した要素をマージする
sorted_ary = []
while ary_l.length > 0 || ary_r.length > 0
sorted_ary <<
if ary_l.length == 0
ary_r.shift
elsif ary_r.length == 0
ary_l.shift
elsif ary_l[0] > ary_r[0]
ary_r.shift
else
ary_l.shift
end
end
sorted_ary
end
p merge_sort([8, 5, 9, 2, 6, 3, 7, 1, 4])
# > [1, 2, 3, 4, 5, 6, 7, 8, 9]
処理のイメージ図(分割)
分割する様子を図にしました。
すべて分割し終わってからマージするのではなく、左の数字の順に分割とマージを繰り返します。
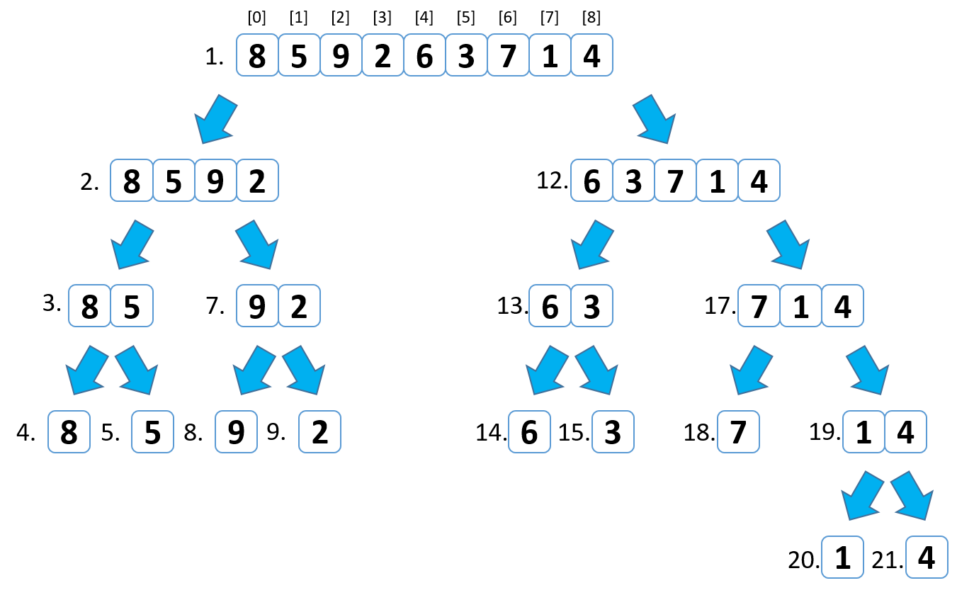
処理のイメージ図(マージ)
右のカッコ内の計算はary_lとary_rを比較してsorted_aryへ挿入する処理の回数です。
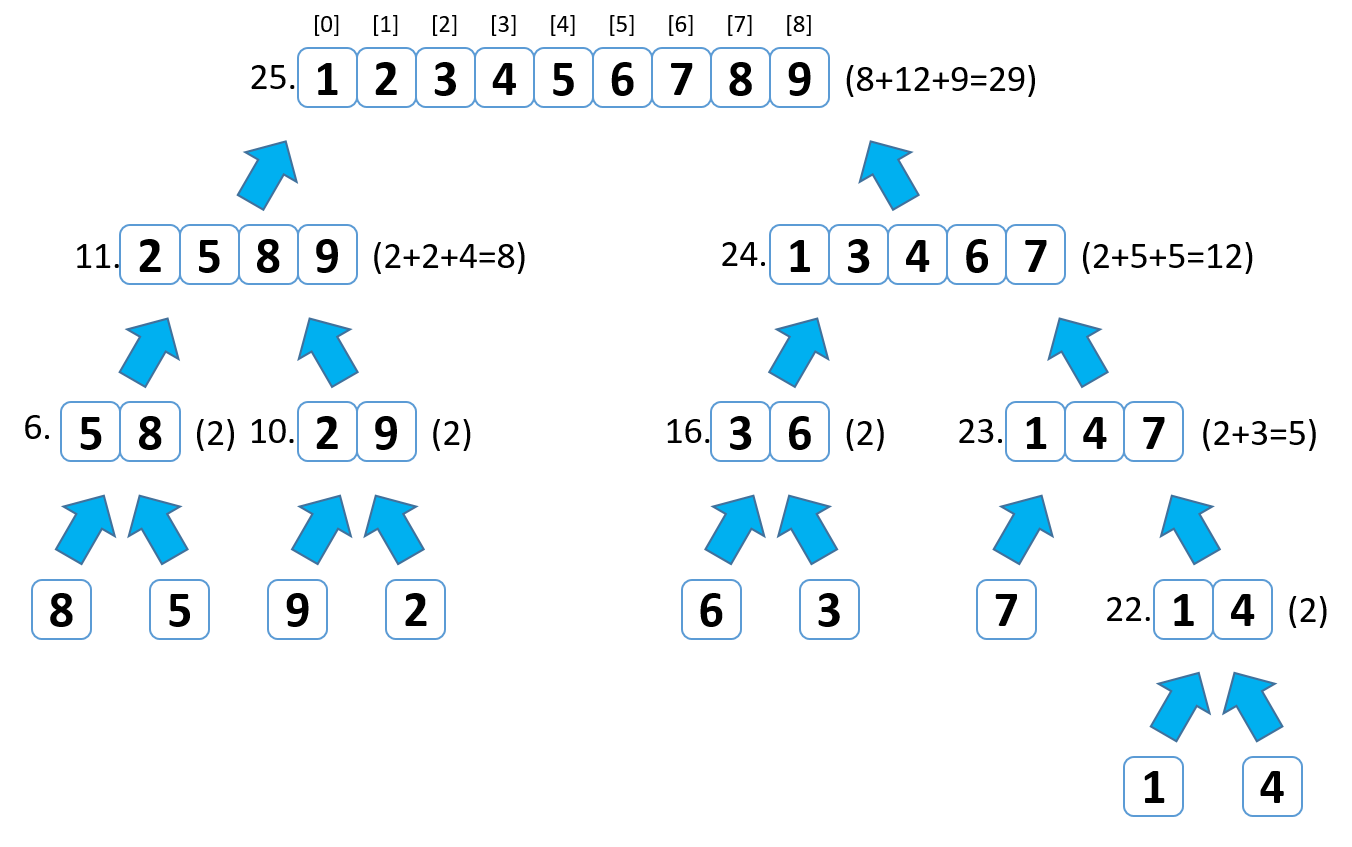
処理の流れ(詳細)
merge_sort([8, 5, 9, 2, 6, 3, 7, 1, 4])を実行する- 1.を左右に分割した左の配列で
merge_sort([8, 5, 9, 2])を実行する - 2.を左右に分割した左の配列で
merge_sort([8, 5])を実行する - 3.を左右に分割した左の配列で
merge_sort([8])を実行する
要素数が1になったので[8]が返り、3.のary_l = [8]になる - 3.を左右に分割した右の配列で
merge_sort([5])を実行する
要素数が1になったので[5]が返り、3.のary_r = [5]になる ary_l: [8], ary_r: [5]を昇順にマージした結果[5, 8]が返り、2.のary_l = [5, 8]になる- 2.を左右に分割した右の配列で
merge_sort([9, 2])を実行する - 7.を左右に分割した左の配列で
merge_sort([9])を実行する
要素数が1になったので[9]が返り、7.のary_l = [9]になる - 7.を左右に分割した右の配列で
merge_sort([2])を実行する
要素数が1になったので[2]が返り、7.のary_r = [2]になる ary_l: [9], ary_r: [2]を昇順にマージした結果[2, 9]が返り、2.のary_r = [2, 9]になるary_l: [5, 8], ary_r: [2, 9]を昇順にマージした結果[2, 5, 8, 9]が返り、1.のary_l = [2, 5, 8, 9]になる- 1.を左右に分割した右の配列で
merge_sort([6, 3, 7, 1, 4])を実行する - 12.を左右に分割した左の配列で
merge_sort([6, 3])を実行する - 13.を左右に分割した左の配列で
merge_sort([6])を実行する
要素数が1になったので[6]が返り、13.のary_l = [6]になる - 13.を左右に分割した右の配列で
merge_sort([3])を実行する
要素数が1になったので[3]が返り、13.のary_r = [3]になる ary_l: [6], ary_r: [3]を昇順にマージした結果[3, 6]が返り、12.のary_l = [3, 6]になる- 12.を左右に分割した右の配列で
merge_sort([7, 1, 4])を実行する - 17.を左右に分割した左の配列で
merge_sort([7])を実行する
要素数が1になったので[7]が返り、17.のary_l = [7]になる - 17.を左右に分割した右の配列で
merge_sort([1, 4])を実行する - 19.を左右に分割した左の配列で
merge_sort([1])を実行する
要素数が1になったので[1]が返り、19.のary_l = [1]になる - 19.を左右に分割した右の配列で
merge_sort([4])を実行する
要素数が1になったので[4]が返り、19.のary_r = [4]になる ary_l: [1], ary_r: [4]を昇順にマージした結果[1, 4]が返り、17.のary_r = [1, 4]になるary_l: [7], ary_r: [1, 4]を昇順にマージした結果[1, 4, 7]が返り、12.のary_r = [1, 4, 7]になるary_l: [3, 6], ary_r: [1, 4, 7]を昇順にマージした結果[1, 3, 4, 6, 7]が返り、1.のary_r = [1, 3, 4, 6, 7]になるary_l: [2, 5, 8, 9], ary_r: [1, 3, 4, 6, 7]を昇順にマージした結果[1, 2, 3, 4, 5, 6, 7, 8, 9]が最初の呼び出しに返る
フィボナッチ数列問題
フィボナッチ数列とは、次の漸化式で定義される数列です。
- F0 = 0
- F1 = 1
- Fn = Fn-1 + Fn-2 (n ≧ 0)
イタリアの学者レオナルド・フィボナッチが紹介することによって有名になりフィボナッチ数列と呼ばれていますが、それ以前にインドの学者ヘーマチャンドラが発見したそうです。
(参考: Wikipedia フィボナッチ数)
図で表すとこんな感じになっていて、フィボナッチ数列の連続する項の比率は黄金比1 : (1 + √5) / 2 = 1.618... に近づいていきます。
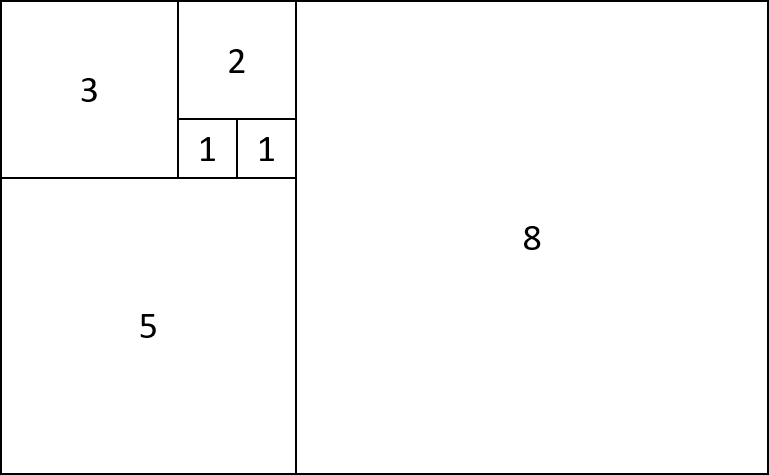
まずはフィボナッチ数列の第n項を求めるプログラムを分割統治法で実装してみます。
処理の流れ
Fnのnが0か1になるまでn-1, n-2を引数に与えて再起呼び出しを行うn=0かn=1まで分割されるとnが返るFn-1とFn-2の返り値を足したものを呼び出し元に返す
サンプルコード
def fib1(n) # n = 0 -> return 0 # n = 1 -> return 1 return n if n < 2 # n が 0 か 1 になるまで再起呼び出しを行う a = fib1(n - 1) b = fib1(n - 2) # 返り値を足して返す a + b end p fib1(4) # > 3 # 第 40 項を計算した時に掛かる時間 start = Time.now p fib1(40) # > 102334155 puts Time.now - start # > 14.8706037
処理のイメージ図(分割)
nが0か1になるまで分割していきます。
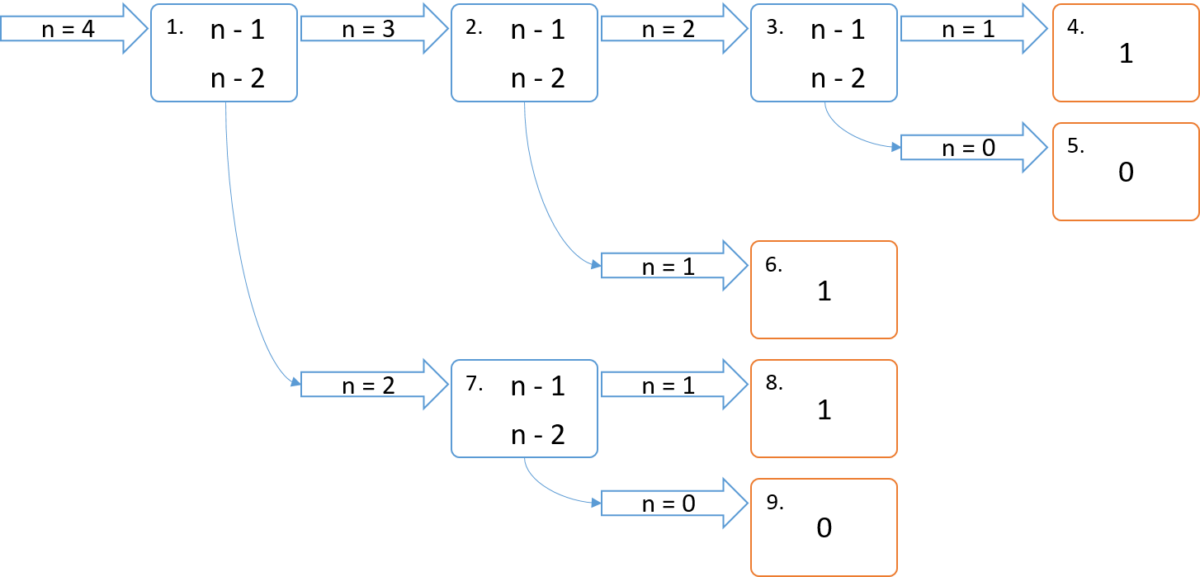
処理のイメージ図(マージ)
nが0か1になるとnが返ってきますので足したものを呼び出し元に返していき、最終的にはF4 = 3となります。
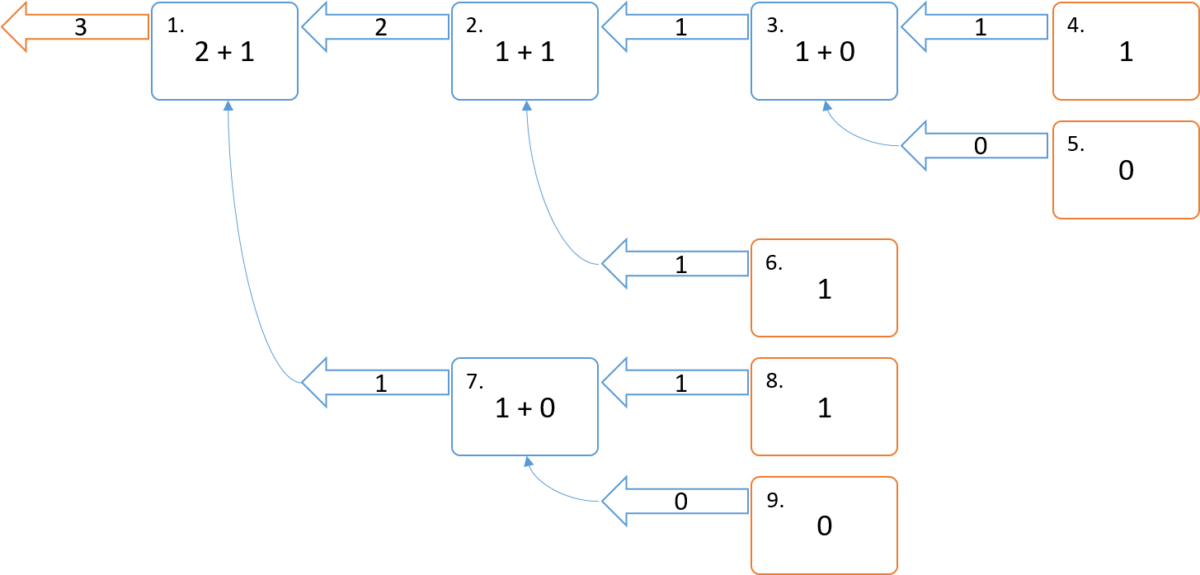
フィボナッチ数列を分割統治法で解くときの問題点
サンプルコードを見ると、フィボナッチ数列の第40項を求めるのに14.87秒かかっています。処理のイメージ図(分割)を見るとわかるようにF4を求めるときにでも同じ計算(F2 = 1)を2回行っています。nが大きくなるにつれて重複の計算箇所がどんどん多くなってしまうので処理速度が遅くなってしまいます。
メモ化で重複の計算をなくする(メモ化再帰)
計算結果を覚えておく方法で同じ計算を繰り返すことを防ぎ、計算回数を削減することが出来ます。
処理の流れ
- 現在わかっている答えをmemoに記録する (n=0 -> 0, n=1 -> 1)
Fnのnが0か1になるまでn-1, n-2を引数に与えて再起呼び出しを行う- memoの答えを調べる
- memoに答えがあるなら答えを返す
- memoに答えがないなら
- 答えが見つかるまで分割する
- 答えが出たらmemoに記録して、
Fn-1とFn-2の返り値を足したものを呼び出し元に返す
サンプルコード1(メモをグローバル変数に記録する)
※ メソッド中のコメントアウト部を表示させるとmemoの変化が確認出来ます。
def fib2(n)
if $memo[n]
# puts "fib2(#{n}) -> $memo[#{n}]: #{$memo[n]}"
return $memo[n]
end
# 再起呼び出し
a = fib2(n - 1)
b = fib2(n - 2)
c = a + b
# puts "$memo[#{n}] = #{a} + #{b} = #{c}, return #{c}"
# 計算結果を$memoに保存して返す
$memo[n] = c
end
# グローバル変数に答えを記録
$memo = [0, 1]
p fib2(4)
# > 3
start = Time.now
p fib2(40)
# > 102334155
puts Time.now - start
# > 8.61e-05
サンプルコード2(返り値の履歴を配列で返してメモにする)
※ メソッド中のコメントアウト部を表示させると返り値の変化が確認出来ます。
def fib3(n) return [0] if n == 0 return [0, 1] if n == 1 ary = fib3(n - 1) ary << ary[-1] + ary[-2] # p ary ary end p fib3(4)[-1] # > 3 start = Time.now p fib3(40)[-1] # > 102334155 puts Time.now - start # > 8.15e-05
処理のイメージ図
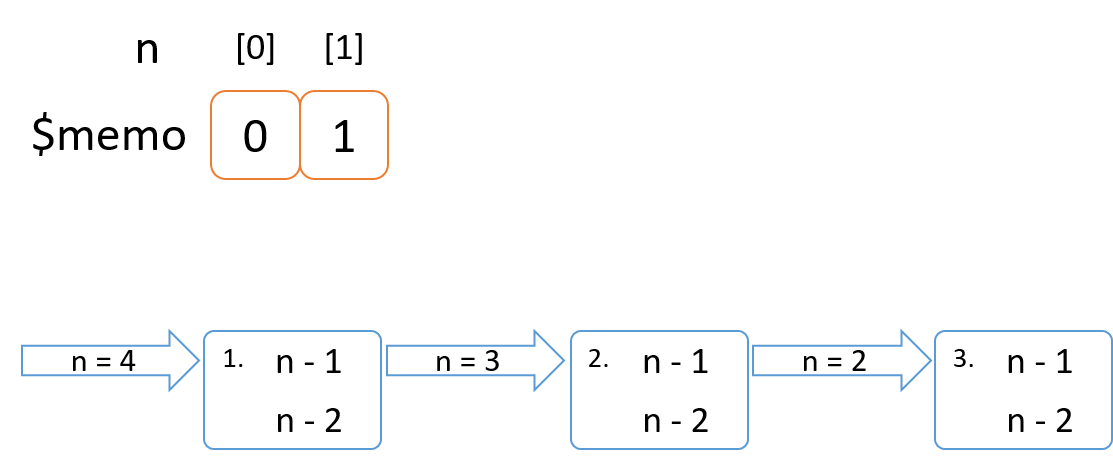
memoに計算に必要な答えがない間は分割していく
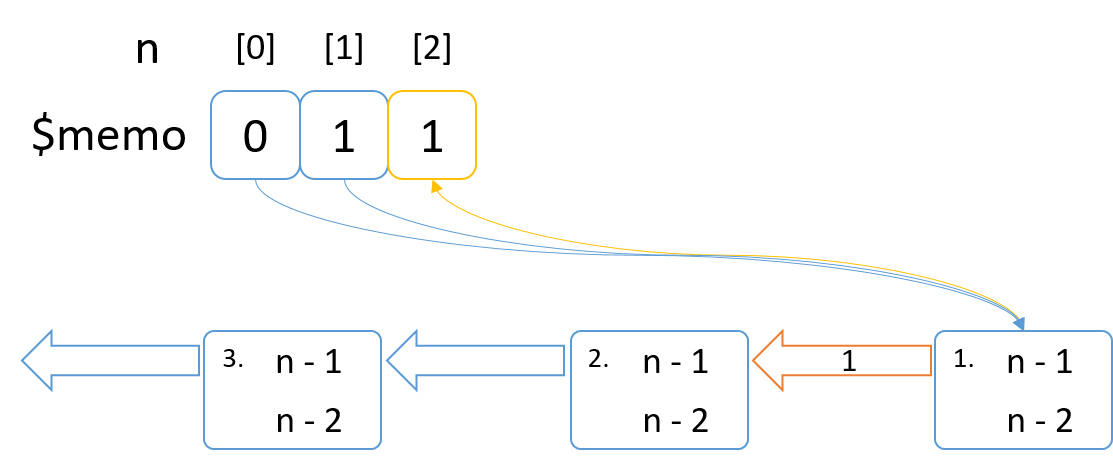
n=2の計算に必要な n=0 -> 0, n=1 -> 1 はmemoに記録されているのでmemoから答えを持ってきてn=2 -> 1を計算する。
n = 2 -> 1をmemoに記録して1を返す。
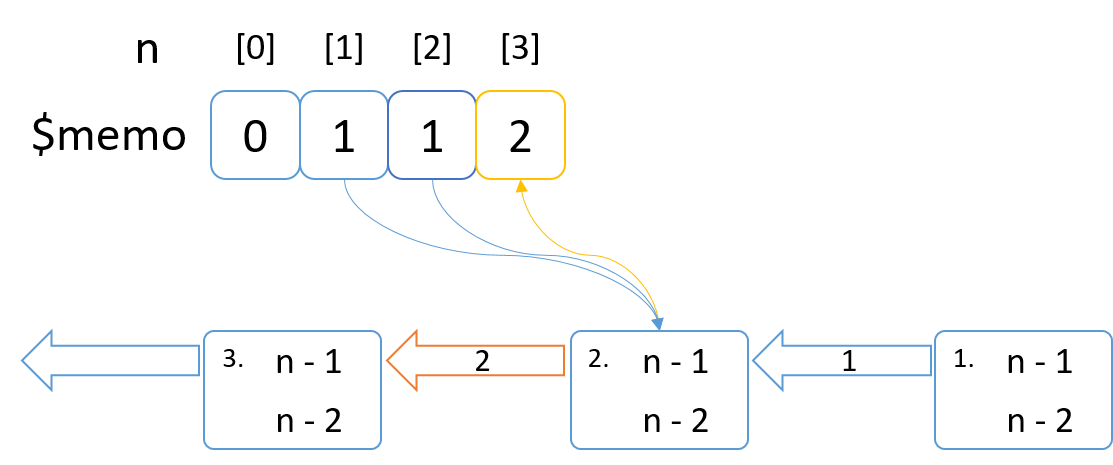
n=3の計算に必要なn=1 -> 1, n=2 -> 1はmemoに記録されているのでmemoから答えを持ってきてn=3 -> 2を計算する。
n = 3 -> 2をmemoに記録して2を返す。
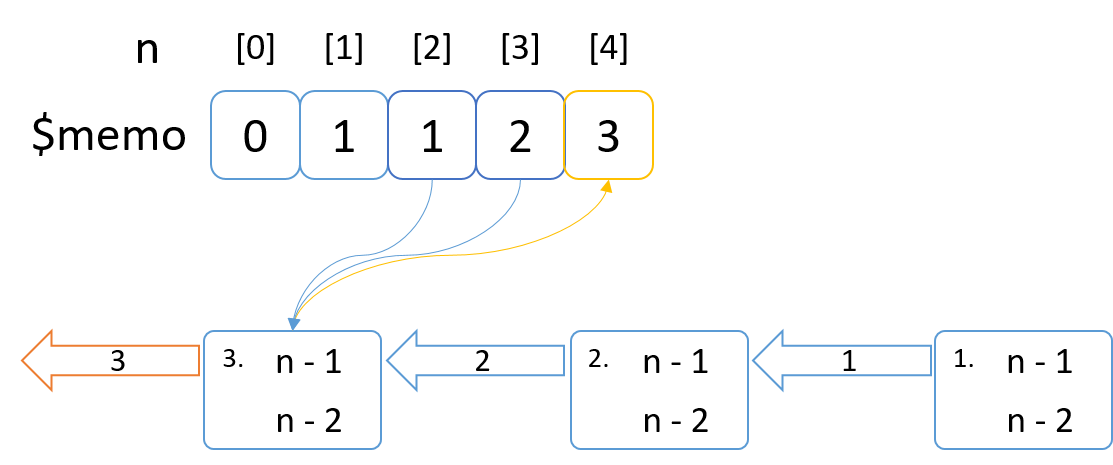
n=4の計算に必要なn=2 -> 1, n=3 -> 2はmemoに記録されているのでmemoから答えを持ってきてn=4 -> 3を計算する。
n = 4 -> 3をmemoに記録して3を返す。
このように分割統治法で、計算結果をメモ化して再利用する方法をメモ化再帰と呼びます。
(トップダウン方式の動的計画法と言われることもあります)
動的計画法
分割統治法も動的計画法も大きな問題を小さな問題に分けて解く方法ですが、分割統治法は「大きな問題を解くために必要な小さな問題は何か」というトップダウンの考え方に対し、動的計画法は「必要かどうかは分からないが今ある小さな問題を解いて積み重ねていく」というボトムアップの考え方になります。
動的計画法の定義を調べてみましたが、厳密な定義があるわけではないようです。
(なのでメモ化再帰は分割統治法でもあり、動的計画法でもあるということでしょうかね。)
動的計画法の定義
細かくアルゴリズムが定義されているわけではなく、下記2条件を満たすアルゴリズムの総称である。
- 帰納的な関係の利用:より小さな問題例の解や計算結果を帰納的な関係を利用してより大きな問題例を解くのに使用する。
- 計算結果の記録:小さな問題例、計算結果から記録し、同じ計算を何度も行うことを避ける。帰納的な関係での参照を効率よく行うために、計算結果は整数、文字やその組みなどを見出しにして管理される。
(引用: Wikipedia 動的計画法)
フィボナッチ数列問題再び
今回はフィボナッチ数列の第n項を動的計画法で求めてみます。
処理の流れ
n=0 -> 0 + n=1 -> 1 が n=2 の答えであることがわかっているので、この計算をn-1回繰り返すことで、第n項を求めることが出来る。
- 現在わかっている答えを記録する
(n=0 -> 0, n=1 -> 1) n - 1回の繰り返し処理を設定する- 記録末尾から2個目の答えと記録末尾の答えを足したものを記録末尾に加える
- 繰り返し処理が終わった時点での記録末尾が第n項の答え
サンプルコード1(配列の末尾2つを計算して末尾に追加する)
def fib4(n)
dp = [0, 1]
return dp[..n] if n < 2
(n - 1).times do
dp << dp[-1] + dp[-2]
end
dp
end
p fib4(4)[-1]
# > 3
start = Time.now
p fib4(40)[-1]
# > 102334155
puts Time.now - start
# > 8.32e-05
サンプルコード2(多重代入を利用して計算する)
def fib5(n)
return n if n < 2
a, b = 0, 1
n.times do
a, b = b, a + b
end
a
end
p fib4(4)
# > 3
start = Time.now
p fib5(40)
# > 102334155
puts Time.now - start
# > 8.85e-05
部分和問題
動的計画法で解ける問題の例として、部分和問題を解いてみます。
色々なバリエーションがありますが、今回はn個の正の整数の配列から、いくつか選んで和をkに出来るかを判定するという問題にします。
問題
n = 3個の正の整数ary = [1, 3, 5]の中からいくつかを選択した和でk = 6を作ることができるかを判定する。
入力例
- 正の整数の数
n = 3 - 作りたい整数
k = 6 - 正の整数の配列
ary = [1, 3, 5]
処理の流れ(全体)
[n+1] × [k+1]の要素をもつ二次元配列の値をfalseにしてdpテーブルを初期化する。
(各行(n+1)は配列の先頭から何個使うかを表す)
(各行の要素(k+1)は使った数の和で出来るかどうかを表す)dp[0][0]をtrueにする(整数を0個選んだ時に0が作れるので)i = 0, 1, 2, …, N-1のループ中にj = 0, 1, 2, …, Kのループを設定してdpテーブルの更新を行う- dp[i + 1][j] = dp[i][j - ary[i]] (ary[i] ≦ j)
ary[i] ≦ jのときはdp[i][j - ary[i]]の値になる - dp[i + 1][j] = dp[i][j] (ary[i] > j)
ary[i] > jのときはdp[i][j]の値になる
- dp[i + 1][j] = dp[i][j - ary[i]] (ary[i] ≦ j)
サンプルコード
n = 3
k = 6
ary = [1, 3, 5]
# dpテーブルの生成・初期化
dp = Array.new(n + 1) { Array.new(k + 1, false) }
# 何も選ばなければ 0 が作れる
dp[0][0] = true
# 二重ループでdpテーブル更新
0.upto(n - 1) do |i|
0.upto(k) do |j|
dp[i + 1][j] = if ary[i] <= j
dp[i][j - ary[i]]
else
dp[i][j]
end
end
end
# ary の先頭から n 個を使って k が作れるか?
p dp[n][k]
# > true
pp dp
# > [[true, false, false, false, false, false, false],
# > [true, true, false, false, false, false, false],
# > [true, true, false, true, true, false, false],
# > [true, true, false, true, true, true, true]]
処理の流れ(詳細)
まずはループに入る前の初期化の処理です
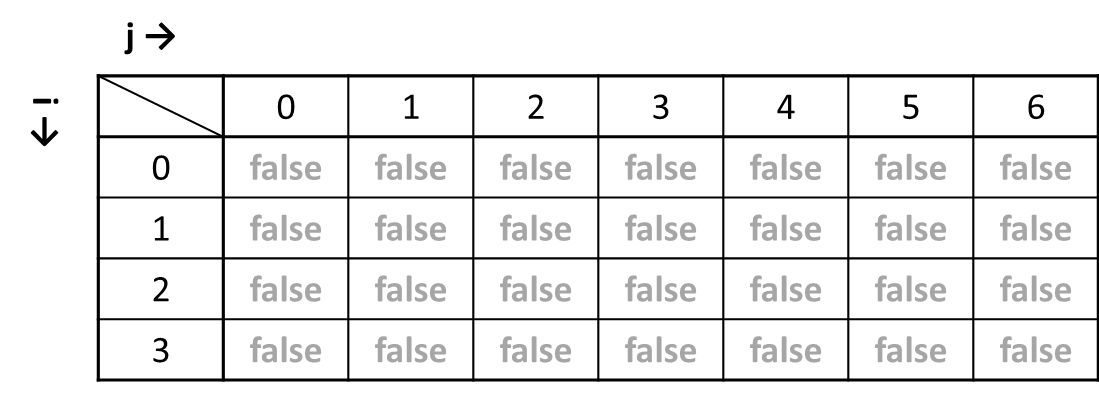
[n+1] × [k+1]の要素をもつ二次元配列の値をfalseにしてdpテーブルを初期化する。
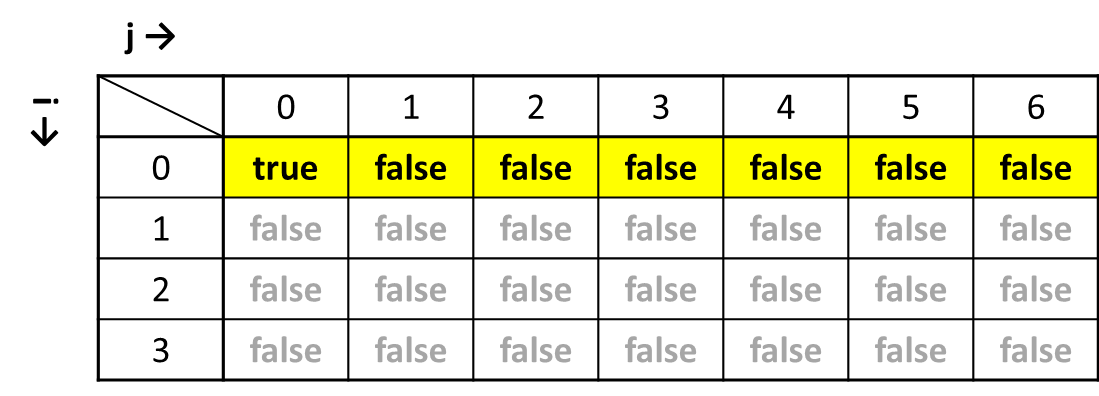
dp[0][0] = trueにします。
i=0(配列から数字を選ばなかった)のとき、和で0を作ることができます。
ここからi = 0, 1, 2, …, N-1 のループ中に j = 0, 1, 2, …, K の二重ループを回します

i=0, j=0のときary[i] > jなので
dp[i + 1][j] = dp[i][j]
i=0, j = 1, 2, 3, 4, 5, 6のときary[i] ≦ jなので
dp[i + 1][j] = dp[i][j - ary[i]]
配列の先頭から1個[(0), 1]を使った組み合わせの和で[0, 1]を作ることができる
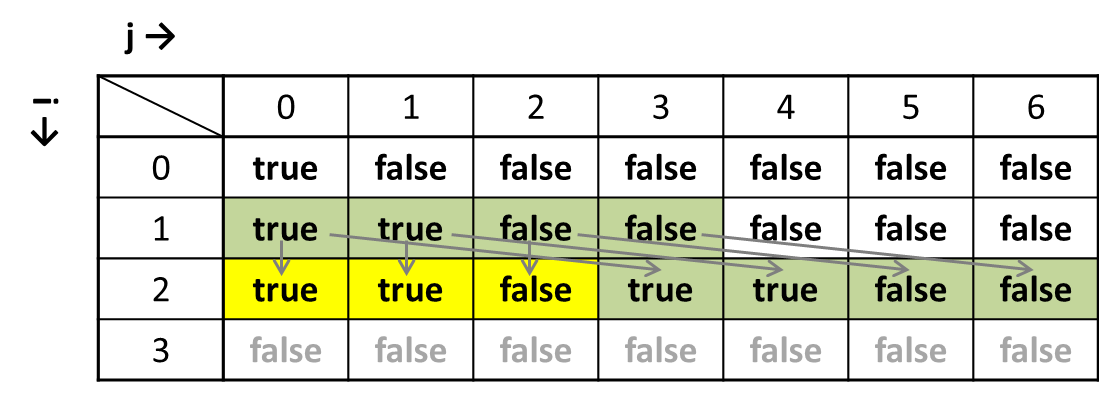
i=1, j=0, 1, 2のときary[i] > jなので
dp[i + 1][j] = dp[i][j]
i=1, j = 3, 4, 5, 6のときary[i] ≦ jなので
dp[i + 1][j] = dp[i][j - ary[i]]
配列の先頭から2個[(0), 1, 3]を使った組み合わせの和で[0, 1, 3, 4]を作ることができる
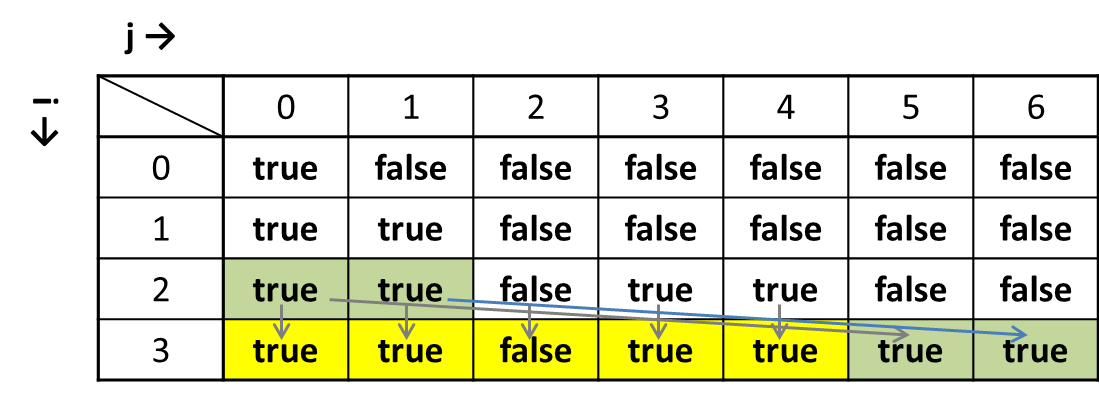
i=2, j=0, 1, 2, 3, 4のときary[i] > jなので
dp[i + 1][j] = dp[i][j]
i=2, j = 5, 6のときary[i] ≦ jなので
dp[i + 1][j] = dp[i][j - ary[i]]
配列の先頭から3個[(0), 1, 3, 5]を使った組み合わせの和で[0, 1, 3, 4, 5, 6]が作れる
ループ終了
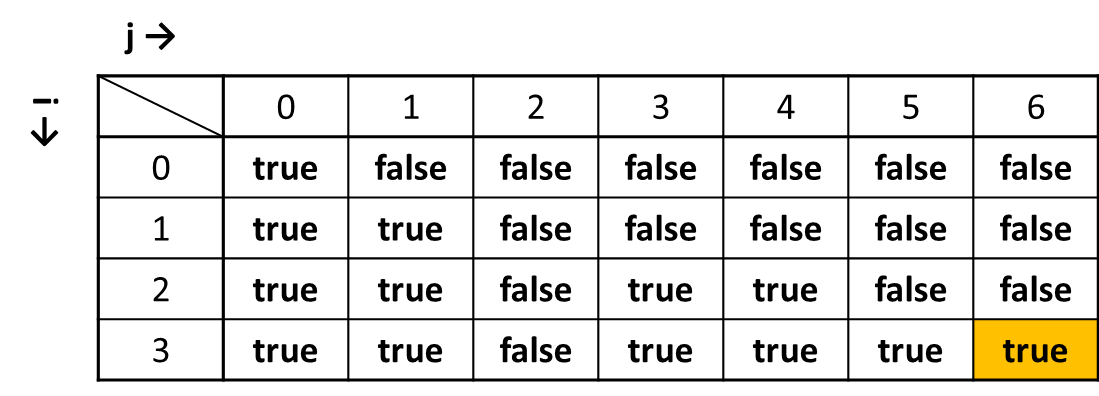
dp[n][k](dp[3][6])を参照する
ary[1, 3, 5]の先頭からn=3個を使った組み合わせの和でk=6を作ることができるか?
> true
今回のまとめ
- 分割統治法
- 求めたい大きな問題から解決できるサイズまで問題を分割することにより、トップダウン方式で問題を解くことができる
- 不要な小問題を解くことはないが、同じ小問題を何度も解くことがある
- メソッド(関数)を再帰的に定義することで実装することができる
- 動的計画法
- 小問題の解を再利用することにより、ボトムアップ方式で大きな問題を解くことができる
- 同じ小問題を何度も解くことはないが、必要の無い小問題を解くことがある
- ループ処理を利用して実装することができる

今回紹介した以外にも、ハノイの塔問題・最短経路数え上げ問題・ナップサック問題など色々な有名な問題がありますので、挑戦してみるのも良いかもしれませんね!




