今回はpaiza リアルイベント問題セット 「雪だるま作り」 (paizaランク A 相当)を解説します。
ランダムな数列から2つを取り出して足し合わせたときに、指定された値以上になる、最大組み合わせ数はいくつか?を答える問題です。
雪だるま作り (paizaランク A 相当)
※ paiza リアルイベント問題セット より
問題
雪が降る季節になりました。パイザくんは雪だるまを作ろうとしています。
パイザくんは N 個の雪玉を作りました。i 番目 (1 ≦ i ≦ N) の雪玉の直径は a_i です。
パイザくんは、2 つの雪玉を組み合わせることで雪だるまを作ろうと考えています。また、パイザくんは、雪だるまの高さが K 以上となるようにしたいと考えています。ここで、雪だるまの高さは、その雪だるまを作るのに使う 2 つの雪玉の直径の和として定義されます。ここで、雪だるまを作る際に組み合わせる 2 つの雪玉は同じ大きさでも構いません。
パイザくんは、できるだけ多くの雪だるまを作りたいと考えています。パイザくんが言う条件を満たすように雪だるまを作っていくとき、最大で何個の雪だるまが作れるかを求めてください。
例)
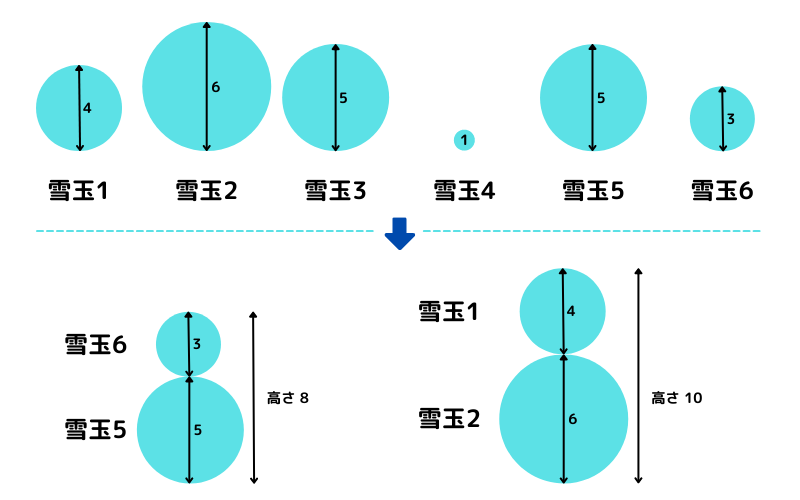
入力例 1 の状況を考えます。このとき、下図のように雪玉を組み合わせると、高さが 8 以上の雪だるまが 2 つ作れます。どのように雪玉を組み合わせても、高さが 8 以上の雪だるまは 3 つは作れないので、この入力例の答えは 2 となります。
入力される値
入力は以下のフォーマットで与えられます。
N K
a_1 a_2 ... a_N
- 1 行目に、パイザくんが作った雪玉の個数を表す整数 N と、雪だるまの高さの条件を表す整数 K が与えられます。
- 2 行目に、i 番目 (1 ≦ i ≦ N) の雪玉の直径を表す N 個の整数 a_i が半角スペース区切りで与えられます。
入力は合計で 2 行となり、末尾に改行が 1 つ入ります。
入力値最終行の末尾に改行が1つ入ります。
期待する出力
条件を満たすように作れる雪だるまの個数の最大値を整数で出力してください。
条件
すべてのテストケースにおいて、以下の条件をみたします。
- 1 ≦ N ≦ 100,000
- 1 ≦ K ≦ 1,000,000,000
- 1 ≦ a_i ≦ 1,000,000,000 (1 ≦ i ≦ N)
- 入力例1
- 6 8
4 6 5 1 5 3
- 出力例1
- 2
- 入力例2
- 10 59
22 29 11 41 42 33 9 27 17 13
- 出力例2
- 3
攻略ポイント
ポイント
- 条件を満たしつつ、雪玉の大きさの無駄が少ない組み合わせを探す。
- 頭と胴体のサイズが同じでも良い。
問題を解く流れ
入出力例をコピペしてヒアドキュメントで変数に代入し、データを確認します。正しく受け取れていれば確認用コードは削除します。
INPUT1 = <<~"EOS" 6 8 4 6 5 1 5 3 EOS OUTPUT1 = <<~"EOS" 2 EOS INPUT2 = <<~"EOS" 10 59 22 29 11 41 42 33 9 27 17 13 EOS OUTPUT2 = <<~"EOS" 3 EOS # 確認用コード p INPUT1 # > "6 8\n4 6 5 1 5 3\n" p OUTPUT1 # > "2\n" p INPUT2 # > "10 59\n22 29 11 41 42 33 9 27 17 13\n" p OUTPUT2 # > "3\n"
続いて問題を解くメソッド( solve メソッドとします)を変数の下に定義します。
まず、入力データを受け取る処理を書きます。
def solve(input_str)
input_lines = input_str.split("\n")
n, k = input_lines[0].split.map(&:to_i)
snow_balls = input_lines[1].split.map(&:to_i)
# 確認用コード
[n, k, snow_balls]
end
# 確認用コード
p solve(INPUT1)
# > [6, 8, [4, 6, 5, 1, 5, 3]]
p solve(INPUT2)
# > [10, 59, [22, 29, 11, 41, 42, 33, 9, 27, 17, 13]]
上記のコードは、次のように短く書くことも出来ます。
def solve(input_str) n, k, *snow_balls = input_str.split.map(&:to_i) # 確認用コード [n, k, snow_balls] end # 確認用コード p solve(INPUT1) # > [6, 8, [4, 6, 5, 1, 5, 3]] p solve(INPUT2) # > [10, 59, [22, 29, 11, 41, 42, 33, 9, 27, 17, 13]]
処理の流れ
- 入力データ受け取り
- 雪玉の数: 整数n ← 今回の実装例では使用しない
- 指定の高さ: 整数k
- 雪玉の直径: 整数の配列snow_balls
- snow_ballsを昇順ソートする
- 雪だるまの数: count = 0 で初期化する
- snow_balls の 雪玉が2個以上の間繰り返すループを設定する
- snow_ballsから最大径の雪玉を取り出し、その直径をbodyとする
- snou_ballsの最小径から順に雪玉を取り出すループを設定する
- 取り出した雪玉の直径をheadとする
- 雪だるまの高さ: (head + body) が 指定された高さ k 以上なら
- count を +1 する
- 最小径から順に取り出すループを抜ける
(内側のループを抜ける)
- countを出力する
探索のイメージはこんな感じです。
INPUT1
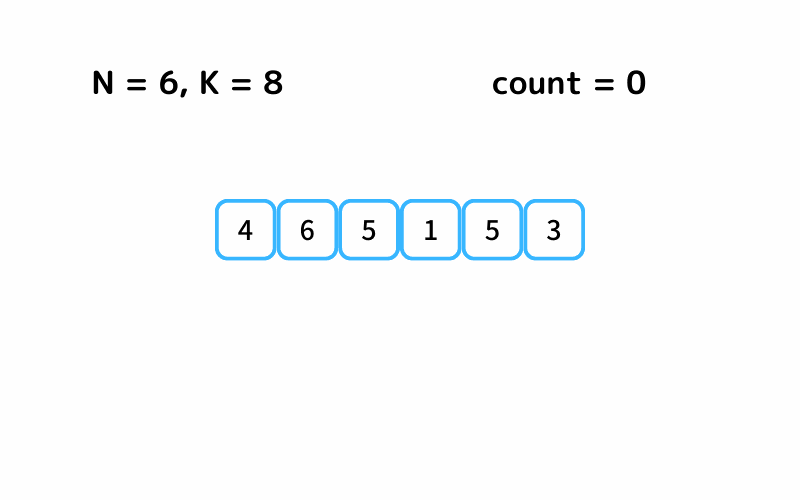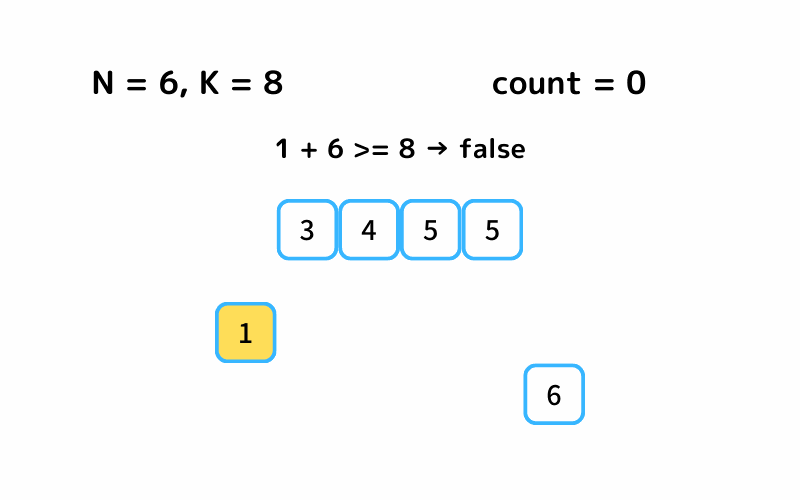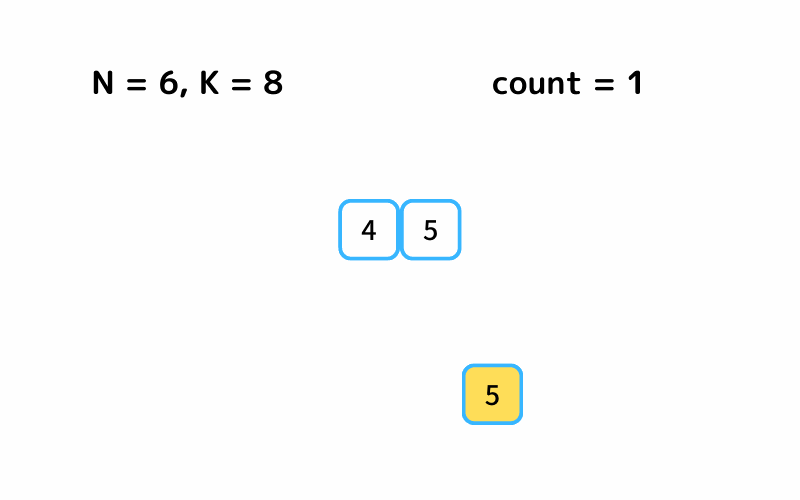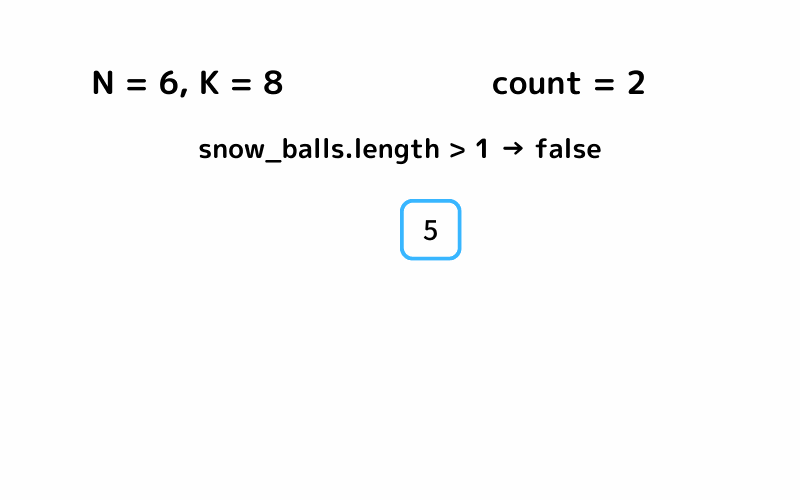
INPUT2
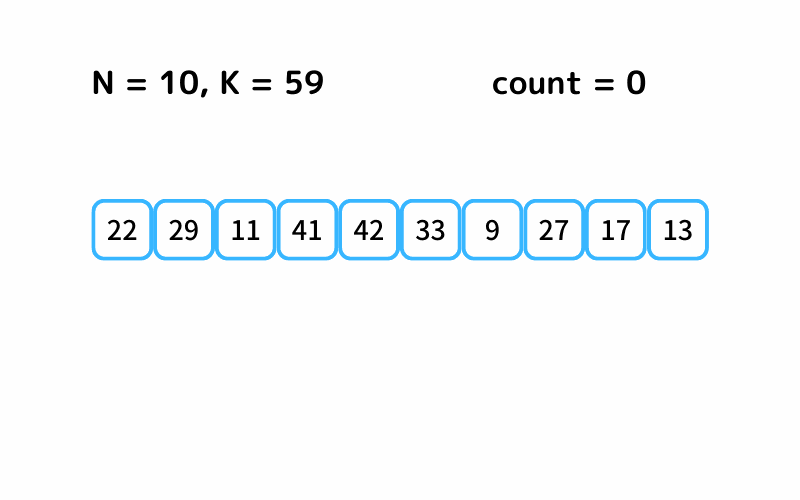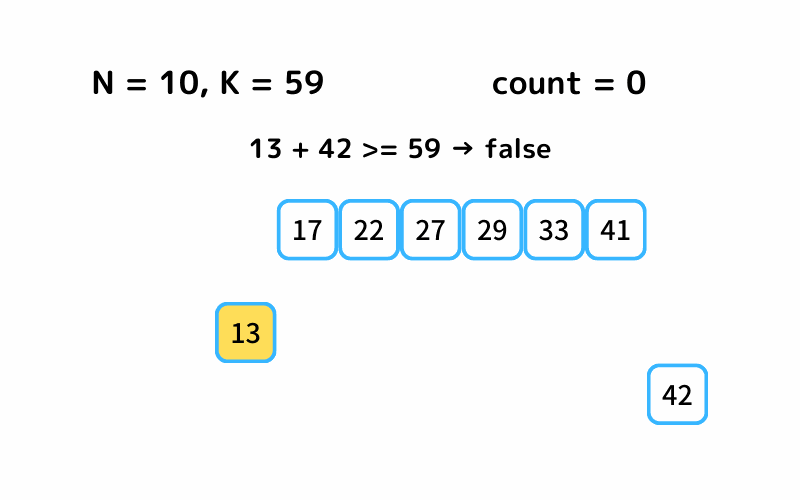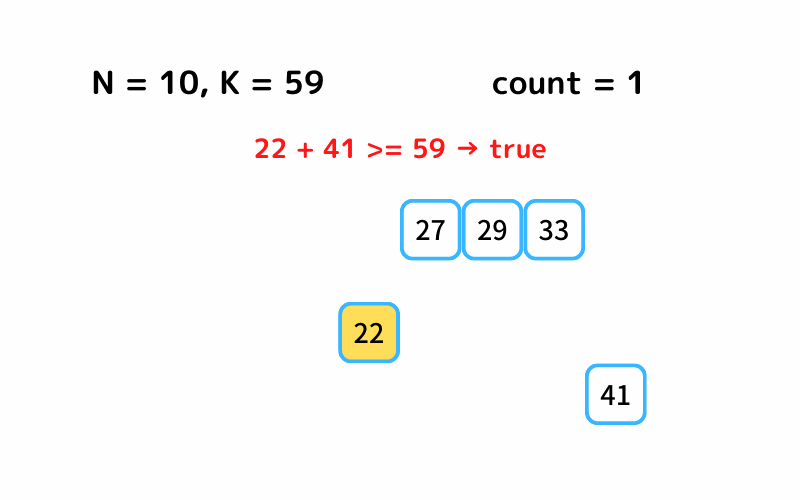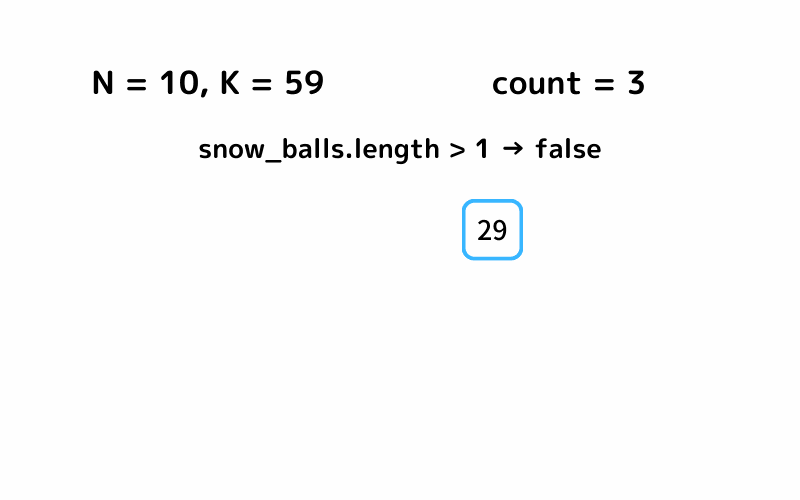
では、以上の処理をsolveメソッドに書いていきます。
def solve(input_str)
# 入力受け取り
n, k, *snow_balls = input_str.split.map(&:to_i)
# 雪玉を昇順ソート
snow_balls.sort!
count = 0
# 雪玉が2個以上ある間ループ
while snow_balls.length > 1
# 最大径の雪玉を取り出し body とする
body = snow_balls.pop
# 最小径から順に取り出すループ
while not snow_balls.empty?
# 最小径の雪玉を取り出し head とする
head = snow_balls.shift
# 高さが k 以上か?
if head + body >= k
# count を +1
count += 1
# 最小径の雪玉を取り出すループを抜ける
break
end
end
end
# 雪だるまの数を返す
count
end
# 確認用コード
p solve(INPUT1)
# > 2
p solve(INPUT1) == OUTPUT1
# > false
p solve(INPUT2)
# > 3
p solve(INPUT2) == OUTPUT2
# > false
このまま提出しても正解なのですが、solve(INPUT1) == OUTPUT1 がtrueになることを確認したいと思います。
def solve(input_str)
# 入力受け取り
n, k, *snow_balls = input_str.split.map(&:to_i)
# 雪玉を昇順ソート
snow_balls.sort!
count = 0
# 雪玉が2個以上ある間ループ
while snow_balls.length > 1
# 最大径の雪玉を取り出し body とする
body = snow_balls.pop
# 最小径から順に取り出すループ
while not snow_balls.empty?
# 最小径の雪玉を取り出し head とする
head = snow_balls.shift
# 高さが k 以上か?
if head + body >= k
# count を +1
count += 1
# 最小径の雪玉を取り出すループを抜ける
break
end
end
end
# 雪だるまの数を文字列に変換して末尾に改行を追加
count.to_s << "\n"
end
# 確認用コード
p solve(INPUT1)
# > "2\n"
p solve(INPUT1) == OUTPUT1
# > true
p solve(INPUT2)
# > "3\n"
p solve(INPUT2) == OUTPUT2
# > true
確認用コードを標準入力からのデータ受け取りに変更、標準出力をpメソッドからputsメソッドに変更して、動作確認をしたら提出します。(STDIN.readの入力終了は Ctrl+D)
Ruby 解答コード
def solve(input_str)
# 入力受け取り
n, k, *snow_balls = input_str.split.map(&:to_i)
# 雪玉を昇順ソート
snow_balls.sort!
count = 0
# 雪玉が2個以上ある間ループ
while snow_balls.length > 1
# 最大径の雪玉を取り出し body とする
body = snow_balls.pop
# 最小径から順に取り出すループ
while not snow_balls.empty?
# 最小径の雪玉を取り出し head とする
head = snow_balls.shift
# 高さが k 以上か?
if head + body >= k
# count を +1
count += 1
# 最小径の雪玉を取り出すループを抜ける
break
end
end
end
# 雪だるまの数を文字列に変換して末尾に改行を追加
count.to_s << "\n"
end
puts solve(STDIN.read)
Ruby 別解
二分探索を使って解くこともできます。
要素数(雪玉の数)がもっと多くなった場合はこちらの方が早いかもしれませんが、今回の問題の条件で大きな差は見られませんでした。
def solve(input_str)
# 入力受け取り
n, k, *snow_balls = input_str.split.map(&:to_i)
# 雪玉を昇順ソート
snow_balls.sort!
count = 0
# 雪玉が2個以上ある間繰り返す
while snow_balls.length > 1
# 最大径の雪玉を取り出し body とする
body = snow_balls.pop
# 高さが k 以上になる雪玉のうち最小径の index を返す
idx = snow_balls.bsearch_index { |head| head + body >= k }
# nil が帰ってきたら雪だるまは作れない
break if idx.nil?
# count を +1
count += 1
# 今回使用した雪玉の次に大きい雪玉を最小径とする
snow_balls = snow_balls[idx + 1..]
end
# 雪だるまの数を文字列に変換して末尾に改行を追加
count.to_s << "\n"
end
puts solve(STDIN.read)
Python3 解答例
Pythonでは両端キューモジュールcollections.dequeを使いましょう。
Pythonでもリストを両端キューのように使うことができますが、配列先頭に対する要素追加・削除がとても遅くなります。
今回の問題では正解できることを確認しましたが、collections.dequeを使った方が効率的です。
リストを両端キューのように使う例(非推奨)
def solve1(input_str):
# 入力受け取り
n, k, *snow_balls = map(int, input_str.split())
# snow_balls 昇順ソート
snow_balls.sort()
count = 0
# 雪玉が2個以上ある間ループ
while len(snow_balls) > 1:
# 最大径の雪玉を取り出し body とする
body = snow_balls.pop()
# 最小径から順に取り出すループ
while snow_balls:
# 最小径の雪玉を取り出し head とする
head = snow_balls.pop(0)
# 高さが k 以上か?
if head + body >= k:
# count を +1
count += 1
# 最小径の雪玉を取り出すループを抜ける
break
return count
print(solve1(open(0).read()))
collections.deque を使う例(推奨)
from collections import deque
def solve2(input_str):
# 入力受け取り
n, k, *snow_balls = map(int, input_str.split())
# snow_balls 昇順ソート, deque オブジェクト生成
snow_balls = deque(sorted(snow_balls))
count = 0
# 雪玉が2個以上ある間ループ
while len(snow_balls) > 1:
# 最大径の雪玉を取り出し body とする
body = snow_balls.pop()
# 最小径から順に取り出すループ
while snow_balls:
# 最小径の雪玉を取り出し head とする
head = snow_balls.popleft()
# 高さが k 以上か?
if head + body >= k:
# count を +1
count += 1
# 最小径の雪玉を取り出すループを抜ける
break
return count
print(solve2(open(0).read()))
今回のまとめ
今回の問題では雪だるまの数が合っていれば良いので、組み合わせのパターンが複数ある場合があります。
その中でも、最も大きい雪玉から順に取り出し、条件を満たす雪玉を小さい方から順に探す方法が最善であると考えて実装しました。

今回のようにその場その場で最も適していると思われるものを選択していくアルゴリズムを貪欲法と言います。
そういえば貪欲法の解説を書いていないので、近々書きたいと思います。




