paiza プログラミング

[Ruby|Python]paiza リアルイベント問題セット 十億連勝 (paizaランク S 相当)

paiza解説_十億連勝

今回はpaiza リアルイベント問題セット 「十億連勝」 (paizaランク S 相当)を解説します。

nステージの各ステージで不特定回数の試合があり、敗退時はそのステージが終了するというルールがあるときに、最大連勝数がxになる勝敗の組み合わせ数の下９桁を答える問題です。

十億連勝 (paizaランク S 相当)

※ paiza リアルイベント問題セット より

問題

あなたは、ゲーム会社 PAIZA でゲームを作っているエンジニアです。あなたは、今、新しい格闘ゲームを作っています。

あなたが作っているゲームは、N 個のステージからなります。 i 番目 (1 ≦ i ≦ N) のステージでは、A_i 回の試合が行われます。次の図は、入力例 1 の場合のゲームのイメージを表します。

試合の例問題図1

ゲームのプレイヤーは、それぞれのステージの試合を順に行っていきます。しかし、ステージの途中で試合に負けた場合、そのステージにまだ残っている試合があっても、強制的に次のステージに進んでしまいます。

たとえば、下の図の例では、1 番目のステージの第 2 試合で負けているので、1 番目のステージの第 3 試合を迎えること無く 2 番目のステージに進んでしまいます。

試合の例

問題図2

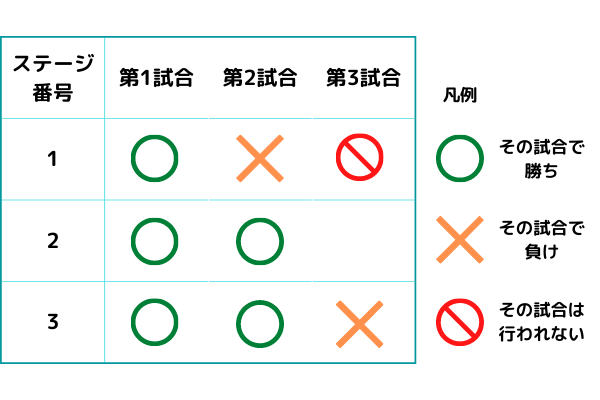
あなたは、このゲームに隠し要素を付けることにしました。その隠し要素とは、「1 番目のステージからはじめ、N 個すべてのステージを終えた時点で、それまでの最大の連勝数がちょうど X だった場合、ボーナスステージが出現する」というものです。

ここで、連勝数とは、連続して勝った試合の数のことを指します。先程の図の場合、最大の連勝数は、第 2 ステージの第 1 試合から第 3 ステージの第 2 試合までで連続して勝っているため、 4 になります。

あなたは、隠し要素の条件を満たすようにゲームをプレイしていく方法が何通りあるかが気になりました。そこで、隠し要素の条件を満たすプレイの仕方の総数をゲームのデバッグ画面に出力することにしました。しかし、デバッグ画面には 9 桁の整数までしか表示することが出来ません。そこで、条件を満たす通り数の下 9 桁を求めてください。

例)

入力例 1 の場合、隠し要素の条件を満たすプレイの仕方の総数は全部で 7 通りあります。これは 9 桁より少ないので、そのまま 7 と答えてください。

入力例 3 の場合、隠し要素の条件を満たすプレイの仕方の総数は全部で 3,247,159,393 通りあります。この場合、下 9 桁である 247159393 と答えてください。

入力される値

N X
A_1
A_2
...
A_N

  • 1 行目に、ゲームのステージを表す整数 N と、隠し要素の条件を表す整数 X がこの順に半角スペース区切りで与えられます。
  • 続く N 行のうちの i 行目 (1 ≦ i ≦ N) には、i 番目のステージでの試合数を表す整数 A_i が与えられます。
  • 入力は合計で N + 1 行となり、入力値最終行の末尾に改行が 1 つ入ります。

入力値最終行の末尾に改行が１つ入ります。

期待する出力

隠し要素の条件を満たすようにゲームをプレイしていく方法の通り数の下 9 桁を、整数で出力してください。

条件

すべてのテストケースにおいて、以下の条件をみたします。

  • 1 ≦ N ≦ 4,000
  • 0 ≦ X ≦ 1,000,000,000
  • 0 ≦ A_i ≦ 1,000,000,000 (1 ≦ i ≦ N)
入力例1
3 4
3
2
3
出力例1
7
入力例2
5 1
1
1
1
1
1
出力例2
12
入力例3
14 6
8
5
9
7
6
9
0
9
8
2
8
1
4
10
出力例3
247159393
攻略ポイント

ポイント

  • 動的計画法でパターンを整理する

動的計画法

問題を解く流れ

まずはINPUT1の連勝状態を全探索した表を見てみましょう。

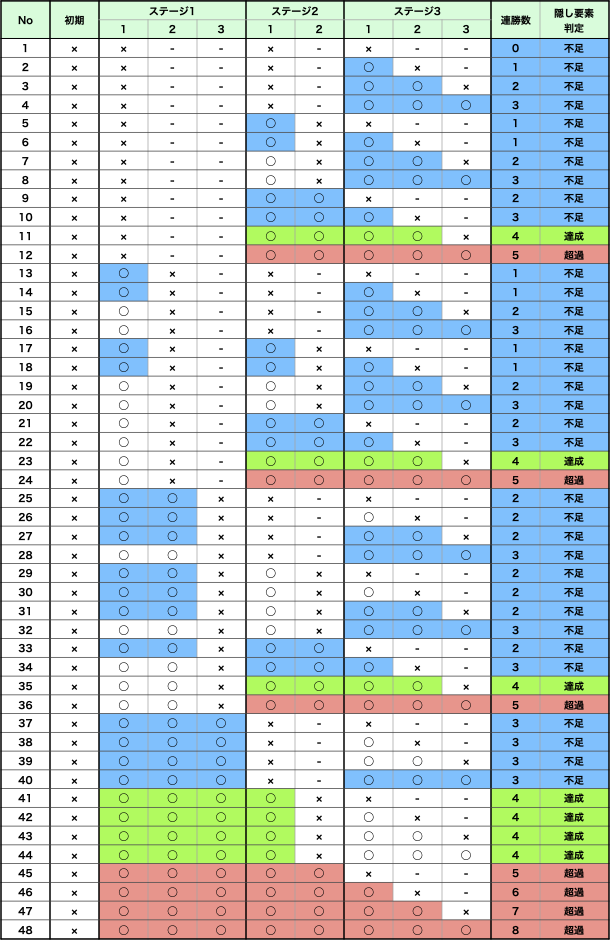
十億連勝全探索

最大連勝数が4となるパターンは7つあることがわかりますが、全探索してしまうと膨大な計算量になってしまうことは明らかなので、動的計画法で考えてみます。

各ステージ毎の終了状態を見ると、下記のようになっています。

  • 連勝数x未満で負け → 隠しチャンスあり
  • 連勝数x丁度で負け → 隠しチャンスあり
  • 連勝数x未満で勝ち越し → 隠しチャンスあり
  • 連勝数x超過で勝ち → 隠しチャンスなし

連勝数x を超えると隠し要素のチャンスがなくなるので、隠し要素のチャンスが残っている状態の数を記録して行き、最後に最大連勝数xを達成したパターンを集計します。

全体の処理を整理する

  • 入力データを受け取る
    • ステージ数: 整数n
    • 隠し条件出現の最大連勝数: 整数x
    • 各ステージの試合数: 整数のリストgame_sets
  • 状態の表: ハッシュstate_table を {[0, false] => 1} で初期化する
    （state_table = {[現在の連勝数, 最大x連勝達成フラグ] => この状態になっている数 ）
  • 各ステージgame_setsを先頭から順に参照する
    • 試合がない場合スキップする
      (0 ≦ A_i ≦ 1,000,000,000)
    • 新しい状態statesを既定値0の空のハッシュで初期化する
    • 前回のゲーム終了時の連勝状態を先頭から順に参照する
      • 連勝数x未満で負けのとき
        states[[0, flag]] += count * [games, x - wins].min
      • ゲーム数gamesが必要連勝数(x-wins)を超えているとき、連勝数xを満たして丁度負けるパターン
        states[[0, true]] += count
      • ゲーム数gamesが必要連勝数(x-wins)以下のとき、連勝数x未満で勝ち越すパターン
        states[[wins + games, flag]] += count
    • 前ステージの連勝状況state_tableを現ステージの連勝状況statesで上書きする
  • 隠しステージが出現する状態数bonusを集計する
    ※ 隠しステージ達成flagがtrueの場合、現在連勝数winsが最大連勝数xの場合

処理の流れはこんな感じです。

INPUT1 (最大連勝数 x = 4)

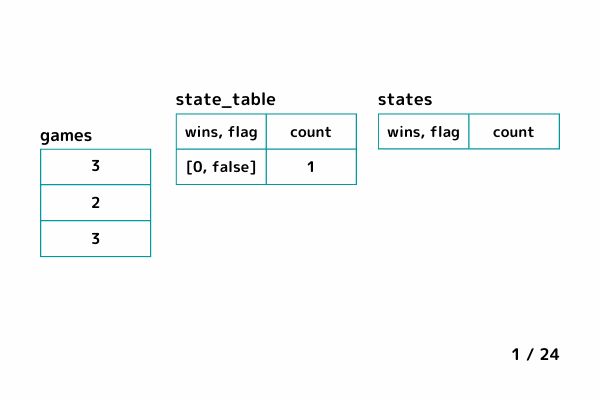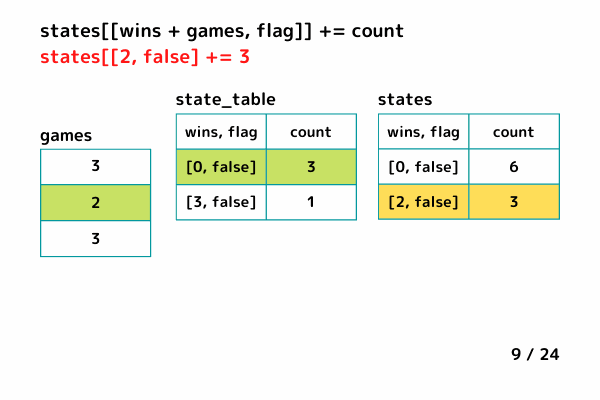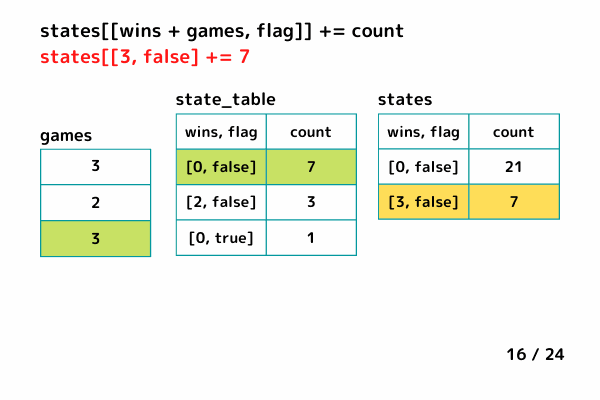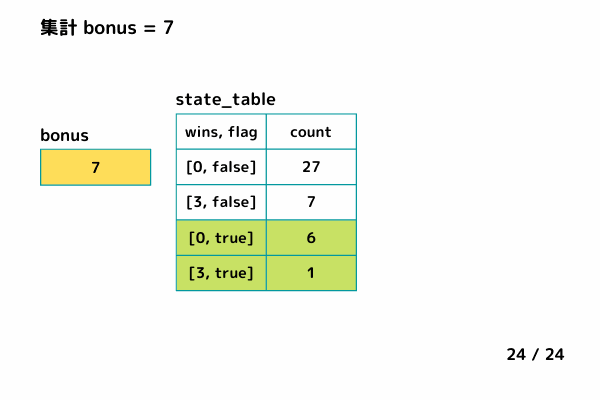
wins_input1

INPUT2 (最大連勝数 x = 1)

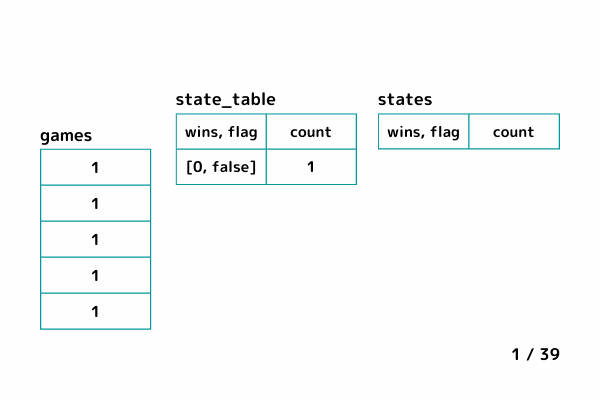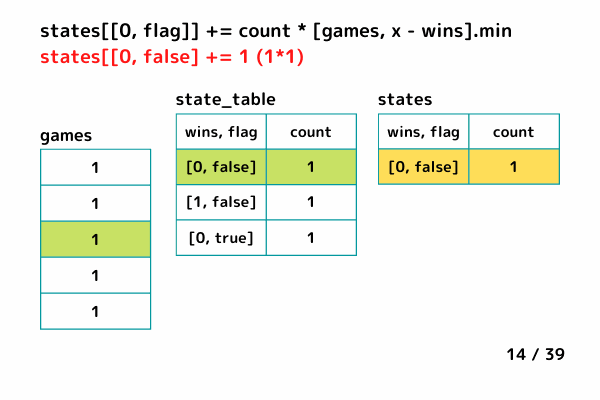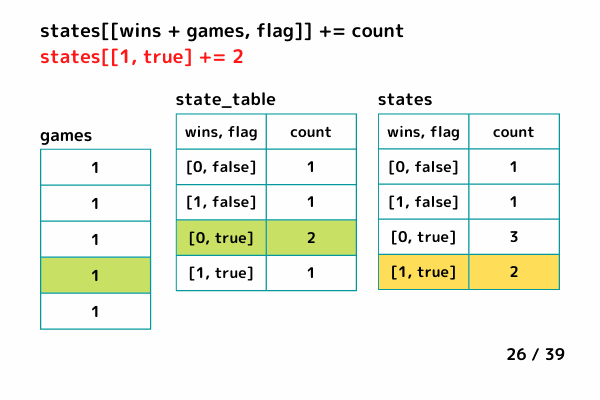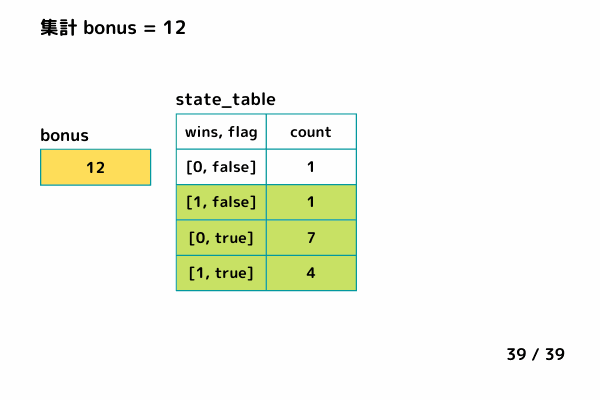
wins_input2

Rubyで実装してみる

入出力例をコピペしてヒアドキュメントで変数に代入し、データを確認します。正しく受け取れていれば確認用コードは削除します。

INPUT1 = <<~"EOS"
  3 4
  3
  2
  3
EOS
OUTPUT1 = <<~"EOS"
  7
EOS

INPUT2 = <<~"EOS"
  5 1
  1
  1
  1
  1
  1
EOS
OUTPUT2 = <<~"EOS"
  12
EOS

# 確認用コード
p INPUT1
# > "3 4\n3\n2\n3\n"
p OUTPUT1
# > "7\n"
p INPUT2
# > "5 1\n1\n1\n1\n1\n1\n"
p OUTPUT2
# > "12\n"

続いて問題を解くメソッド（ solve メソッドとします）を変数の下に定義します。

まず、入力データを受け取る処理を書きます。

def solve(input_str)
  # 下9桁表示用
  d = 1_000_000_000
  # -----------------------------------
  # 入力受け取り
  # -----------------------------------
  # n: ステージ数, x: ボーナス条件, game_sets: 試合のセット数
  n, x, *game_sets = input_str.split.map(&:to_i)

  # 確認用コード
  [n, x, game_sets]
end

# 確認用コード
p solve(INPUT1)
# > [3, 4, [3, 2, 3]]
p solve(INPUT2)
# > [5, 1, [1, 1, 1, 1, 1]]

入力データを正しく受けとれていれば、試合のセット数game_setsを基に、連勝数の状態state_tableを作成します。

def solve(input_str)
  # 下9桁表示用
  d = 1_000_000_000
  # -----------------------------------
  # 入力受け取り
  # -----------------------------------
  # n: ステージ数, x: ボーナス条件, game_sets: 試合のセット数
  n, x, *game_sets = input_str.split.map(&:to_i)

  # -----------------------------------
  # state_table: 連勝状態の表を作成・更新する
  # -----------------------------------
  # state_table 初期化
  # キー: [連勝数, ボーナスフラグ], 値: この状態になっている数
  state_table = { [0, false] => 1 }

  # ステージ分 繰り返す
  game_sets.each do |games|
    # 確認用コード
    p state_table

    # 試合がない場合スキップ
    next if games == 0

    # 新しい状態の初期値を 0 に設定
    states = Hash.new(0)
    # 前回のゲーム終了時の連勝状態を先頭から順に参照する
    # wins: 連勝数, flag: ボーナスフラグ, count: カウント
    state_table.each do |(wins, flag), count|
      # 連勝数x未満で負けのパターン
      states[[0, flag]] += count * [games, x - wins].min

      if games > x - wins
        # ボーナスを満たして負けるパターン
        states[[0, true]] += count
      else
        # 連勝で終わるパターン
        states[[wins + games, flag]] += count
      end
    end
    # state_table を上書きする
    state_table = states
  end
  # 確認用コード
  state_table
end

# 確認用コード
p solve(INPUT1)
# > {[0, false]=>1}
# > {[0, false]=>3, [3, false]=>1}
# > {[0, false]=>7, [2, false]=>3, [0, true]=>1}
# > {[0, false]=>27, [3, false]=>7, [0, true]=>6, [3, true]=>1}
p solve(INPUT2)
# > {[0, false]=>1}
# > {[0, false]=>1, [1, false]=>1}
# > {[0, false]=>1, [1, false]=>1, [0, true]=>1}
# > {[0, false]=>1, [1, false]=>1, [0, true]=>2, [1, true]=>1}
# > {[0, false]=>1, [1, false]=>1, [0, true]=>4, [1, true]=>2}
# > {[0, false]=>1, [1, false]=>1, [0, true]=>7, [1, true]=>4}

連勝数の状態state_tableが正しく作れていれば、最大連勝数xを達成できるパターンを集計します。

def solve(input_str)
  # 下9桁表示用
  d = 1_000_000_000
  # -----------------------------------
  # 入力受け取り
  # -----------------------------------
  # n: ステージ数, x: ボーナス条件, game_sets: 試合のセット数
  n, x, *game_sets = input_str.split.map(&:to_i)

  # -----------------------------------
  # state_table: 連勝状態の表を作成・更新する
  # -----------------------------------
  # state_table 初期化
  # キー: [連勝数, ボーナスフラグ], 値: この状態になっている数
  state_table = { [0, false] => 1 }

  # ステージ分 繰り返す
  game_sets.each do |games|
    # 試合がない場合スキップ
    next if games == 0

    # 新しい状態の初期値を 0 に設定
    states = Hash.new(0)
    # 前回のゲーム終了時の連勝状態を先頭から順に参照する
    # wins: 連勝数, flag: ボーナスフラグ, count: カウント
    state_table.each do |(wins, flag), count|
      # 連勝数x未満で負けのパターン
      states[[0, flag]] += count * [games, x - wins].min

      if games > x - wins
        # ボーナスを満たして負けるパターン
        states[[0, true]] += count
      else
        # 連勝で終わるパターン
        states[[wins + games, flag]] += count
      end
    end
    # state_table を上書きする
    state_table = states
  end
  # -----------------------------------
  # bonus: 隠しステージが出現する状態を集計する
  # -----------------------------------
  bonus = 0
  # ボーナス発生パターンを集計
  state_table.each do |(wins, flag), count|
    bonus += count if flag || wins == x
  end
  # ボーナス発生パターンの下9桁を返す
  (bonus % d).to_s << "\n"
end

# 確認用コード
p solve(INPUT1)
# > "7\n"
p solve(INPUT1) == OUTPUT1
# > true
p solve(INPUT2)
# > "12\n"
p solve(INPUT2) == OUTPUT2
# > true

最後に提出用のコードに修正します。
確認用コードを標準入力からのデータ受け取りに変更、標準出力をpメソッドからputsメソッドに変更して提出します。（STDIN.readの入力終了は Ctrl+D)

Ruby 解答例
def solve(input_str)
  # 下9桁表示用
  d = 1_000_000_000
  # -----------------------------------
  # 入力受け取り
  # -----------------------------------
  # n: ステージ数, x: ボーナス条件, game_sets: 試合のセット数
  n, x, *game_sets = input_str.split.map(&:to_i)

  # -----------------------------------
  # state_table: 連勝状態の表を作成・更新する
  # -----------------------------------
  # state_table 初期化
  # キー: [連勝数, ボーナスフラグ], 値: この状態になっている数
  state_table = { [0, false] => 1 }

  # ステージ分 繰り返す
  game_sets.each do |games|
    # 試合がない場合スキップ
    next if games == 0

    # 新しい状態の初期値を 0 に設定
    states = Hash.new(0)
    # 前回のゲーム終了時の連勝状態を先頭から順に参照する
    # wins: 連勝数, flag: ボーナスフラグ, count: カウント
    state_table.each do |(wins, flag), count|
      # 連勝数x未満で負けのパターン
      states[[0, flag]] += count * [games, x - wins].min

      if games > x - wins
        # ボーナスを満たして負けるパターン
        states[[0, true]] += count
      else
        # 連勝で終わるパターン
        states[[wins + games, flag]] += count
      end
    end
    # state_table を上書きする
    state_table = states
  end
  # -----------------------------------
  # bonus: 隠しステージが出現する状態を集計する
  # -----------------------------------
  bonus = 0
  # ボーナス発生パターンを集計
  state_table.each do |(wins, flag), count|
    bonus += count if flag || wins == x
  end
  # ボーナス発生パターンの下9桁を返す
  (bonus % d).to_s << "\n"
end

puts solve(STDIN.read)
Python3 解答例

Ruby解答例をPythonに翻訳しました。

def solve(input_str):
    # 下9桁表示用
    d = 1_000_000_000
    # -----------------------------------
    # 入力受け取り
    # -----------------------------------
    # n: ステージ数, x: ボーナス条件, game_sets: 試合のセット数
    n, x, *game_sets = map(int, input_str.strip().split())

    # -----------------------------------
    # state_table: 連勝状態の表を作成・更新する
    # -----------------------------------
    # state_table 初期化
    # キー: (連勝数, ボーナスフラグ), 値: この状態になっている数
    state_table = {(0, False): 1}

    # ステージ分 繰り返す
    for games in game_sets:
        # 試合がない場合スキップ
        if games == 0:
            continue

        # 新しい状態を設定
        states = {}
        # 前回のゲーム終了時の連勝状態を先頭から順に参照する
        # wins: 連勝数, flag: ボーナスフラグ, count: カウント
        for (wins, flag), count in state_table.items():
            # 連勝数x未満で負けのパターン
            key = (0, flag)
            states[key] = states.get(key, 0) + \
                count * min(games, x - wins)

            if games > x - wins:
                # ボーナスを満たして負けるパターン
                key = (0, True)
                states[key] = states.get(key, 0) + count
            else:
                # 連勝で終わるパターン
                key = (wins + games, flag)
                states[key] = states.get(key, 0) + count
        # state_table を上書きする
        state_table = states

    # -----------------------------------
    # bonus: 隠しステージが出現する状態を集計する
    # -----------------------------------
    bonus = 0
    # ボーナス発生パターンを集計
    for (wins, flag), count in state_table.items():
        if flag or wins == x:
            bonus += count
    # ボーナス発生パターンの下9桁を返す
    return str(bonus % d) + "\n"


print(solve(open(0).read()))

今回のまとめ

今回は動的計画法で、直前の連勝の状態と現在の試合数から、現在のステージが終了した時の連勝の状態を計算しました。

動的計画法は、全探索だと膨大な計算量になる場合や、貪欲法では誤回答してしまうようなときに検討してみると良いと思います。


【PR】アルゴリズム学習でお世話になった本


アルゴリズム関連の技術書は大抵C/C++で書かれていますが、ある程度プログラムが出来れば、処理の流れは理解することが出来ます。





通称: 螺旋本。C++で解説されています。AOJ(Aizu Online Judge)を運営している会津大学の渡辺准教授が書いた本です。データ構造や計算量の内容から丁寧に書いてありますのでアルゴリズム学習の最初の参考書としてオススメです。


プログラミングコンテスト攻略のためのアルゴリズムとデータ構造 [ 渡部有隆 ]
posted with カエレバ
楽天市場
Amazon
Yahooショッピング




通称: 蟻本。C++で解説されています。競技プログラミング中級者の定番書と言われていて、競技プログラミングで利用できる色々なアルゴリズムを学ぶことが出来ます。かなり高度な内容も含まれているので1冊分を完全に理解するのにはかなりの時間がかかりそうですが、手元に置いて何度も読み返しています。


プログラミングコンテストチャレンジブック第2版 問題解決のアルゴリズム活用力とコーディングテクニッ [ 秋葉拓哉 ]
posted with カエレバ
楽天市場
Amazon
Yahooショッピング




通称: チーター本。C#, C++, JAVAでTopcoderの問題を解説しています。初心者～中級者向けに書かれているので解説が非常に丁寧です。


最強最速アルゴリズマー養成講座 プログラミングコンテストTopCoder攻略ガイド【電子書籍】[ 高橋 直大 ]
posted with カエレバ
楽天市場
Amazon
Yahooショッピング




Python3でアルゴリズムを解説している本です。講義スタイルの本で、図やフローチャートを使ってアルゴリズムとデータ構造についてしっかりと説明されています。代わりにコードは少なめです。Pythonコードが読めなくても十分理解できると思います。


Pythonで体験してわかるアルゴリズムとデータ構造 [ 西澤 弘毅 ]
posted with カエレバ
楽天市場
Amazon
Yahooショッピング

-paiza, プログラミング
-,

© 2024 じゃいごテック