こんにちは!じゃいごテックのあつしです。
今回は木構造やグラフの探索に用いられる、深さ優先探索(Depth First Search)と、幅優先探索(Breadth First Search)をご紹介します。
アルゴリズムはほぼ同じですが、データ構造にスタック(stack)を使うと深さ優先探索、キュー(queue)を使うと幅優先探索になります。
どちらも全ての要素を探索(全探索)できますが、計算量やメモリ消費を少なくするためには問題に応じて使い分ける必要があります。
最強アルゴリズマー養成講座(通称チーター本)によると下記のような使い分けをすると良いとのことです。
- 深さ優先探索
- 全通りを列挙し、結果をまとめる場合
- 辞書順で最初の解を求める場合
- 幅優先探索
- 最短経路を求める場合
- ある程度近くに求めたい解があることがわかっている場合
深さ優先探索(Depth First Search)
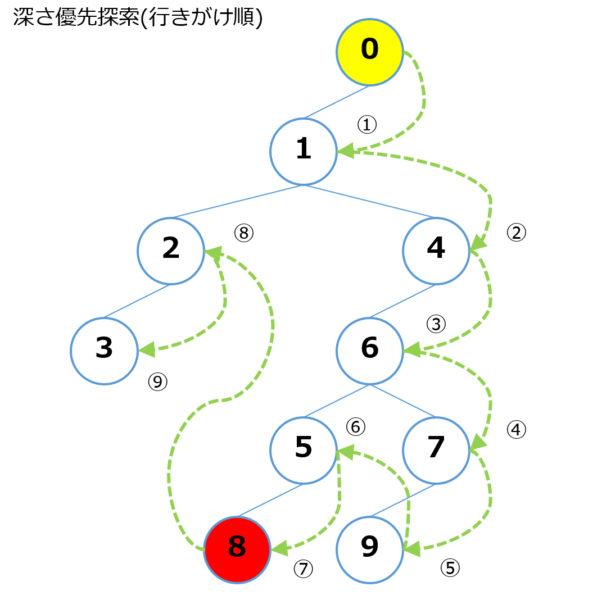
探索開始地点から隣接するノードの突き当りまで探索を行った後、ノードを戻って分岐点があれば分岐点以下の探索を繰り返します。深さ優先探索にはさらに「行きがけ順」「通りがけ順」「帰りがけ順」の探索方法がありますが、今回は「行きがけ順の深さ優先探索」を扱います。
実装例
下図の木構造の [0] から深さ優先探索を行い、 [8] にあるお宝を探索する様子をシミュレーションしてみます。
データ構造
サンプルコード
# スタート位置の設定
start = 0
# お宝の位置の設定 (treasure ≠ start)
treasure = 8
# 要素の繋がり設定
tree = [[1], # [0] は [1] と隣接
[0, 2, 4], # [1] は [0, 2, 4] と隣接
[1, 3], # [2] は [1, 3] と隣接
[2], # [3] は [2] と隣接
[1, 6], # [4] は [1, 6] と隣接
[6, 8], # [5] は [6, 8] と隣接
[4, 5, 7], # [6] は [4, 5, 7] と隣接
[6, 9], # [7] は [6, 9] と隣接
[5], # [8] は [5] と隣接
[7]] # [9] は [7] と隣接
# 探索済みチェック用
searched = Array.new(tree.length, false)
# スタート位置の設定
searched[start] = true
stack = tree[start]
step = 0
# 深さ優先探索
while stack.length > 0
step += 1
puts <<~"EOS"
--------------------
#{step}
探索候補 -> #{stack}
EOS
# 配列末尾から要素を取り出す
node = stack.pop
searched[node] = true
msg = "tree[#{node}] を探索 -> "
if node == treasure
puts msg << "お宝発見!"
# break
else
puts msg << "お宝はありませんでした"
end
puts "探索済みリスト -> #{searched}"
# 隣接ノードのうち未探索を探索候補に入れる
next_nodes = tree[node].select { |node| not searched[node] }
puts "追加候補 -> #{next_nodes}"
next_nodes.each { |node| stack.push(node) }
end
処理の流れ
繰り返し処理に入る前にスタート位置 (0) の設定を行います。
(start ≠ treasure とします)
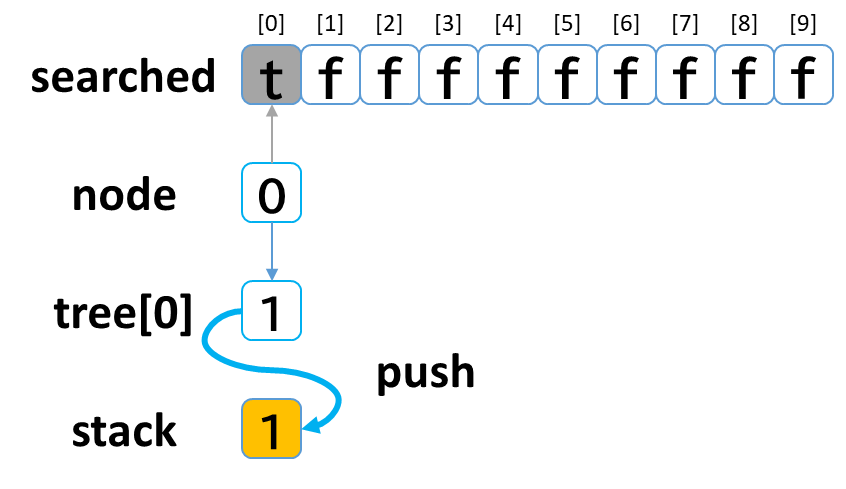
- searched[0] を true にします。
(node[0] を探索済みにします。) - tree[0](node[0]の隣接ノード)を先頭から全て stack に push します。
(初回なのでnode[0]の隣接ノードは未探索です。)
ここから繰り返し処理です。stack が空になるまで繰り返します。
1回目の探索
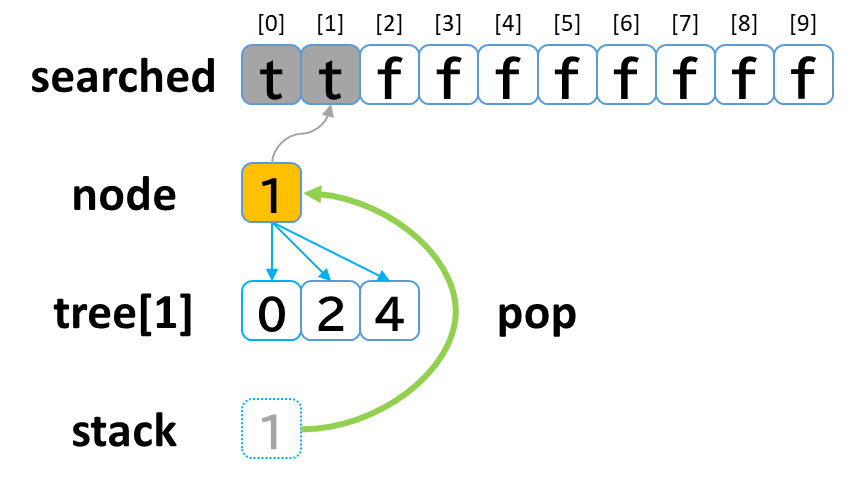
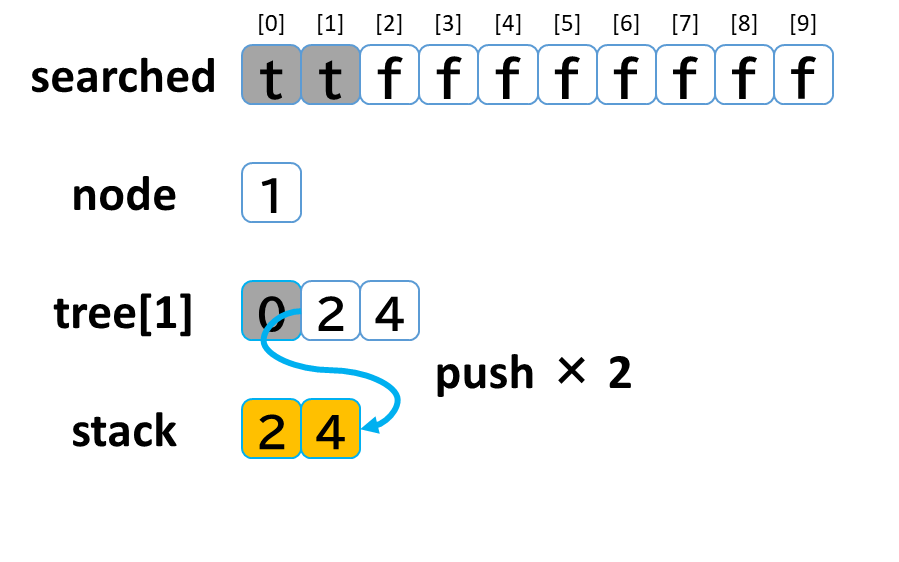
- stack から pop して node に代入します。(node = 1)
- searched[1] を true にします。
- node (1) == treasure (8) -> false でした。
- tree[1] を 参照します。
- tree[1]: [0, 2, 4] のうち、未探索の [2, 4] を stack に push します。
2回目の探索
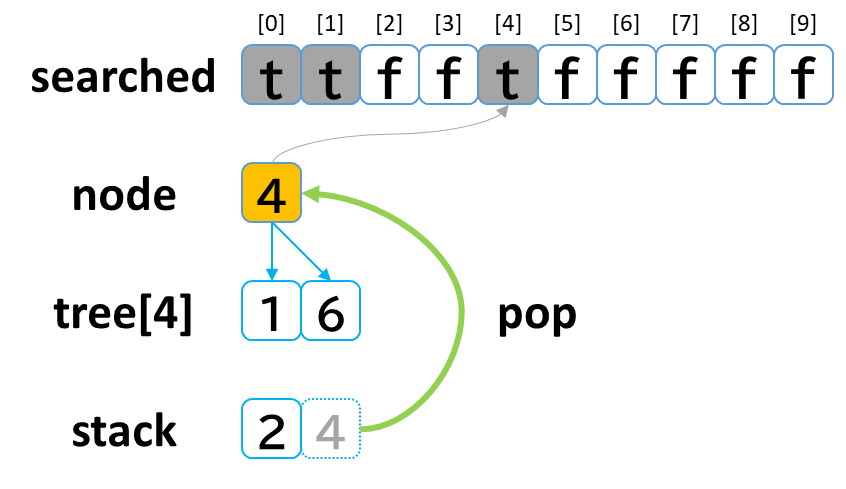
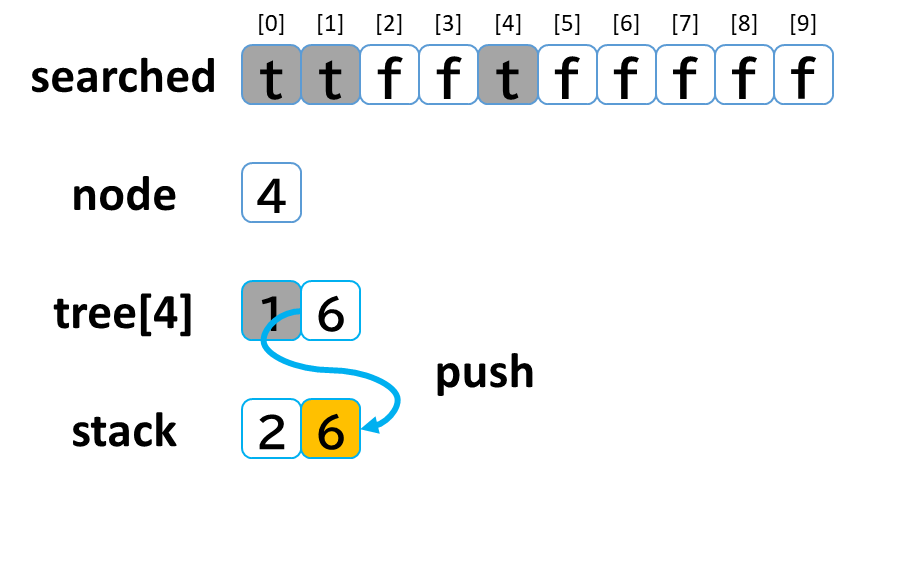
- stack から pop して node に代入します。(node = 4)
- searched[4] を true にします。
- node (4) == treasure (8) -> false でした。
- tree[4] を 参照します。
- tree[4]: [1, 6] のうち、未探索の [6] を stack に push します。
3回目の探索
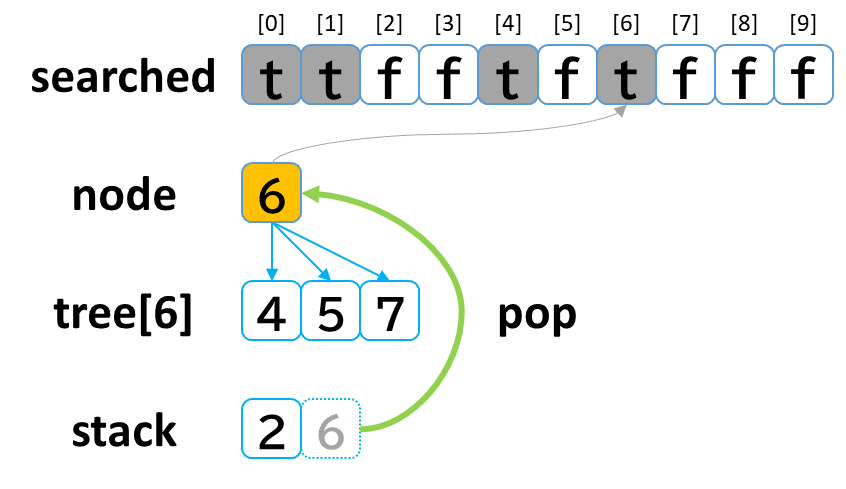
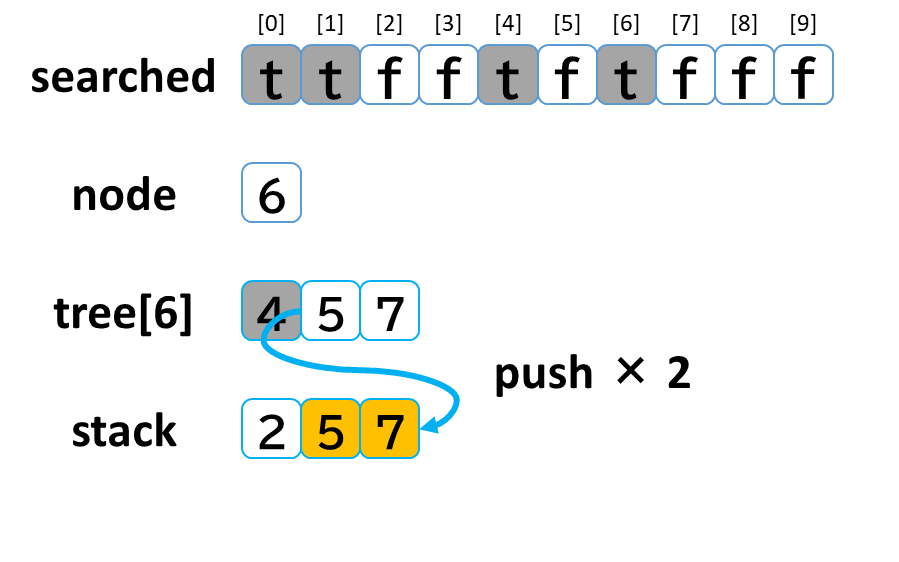
- stack から pop して node に代入します。(node = 6)
- searched[6] を true にします。
- node (6) == treasure (8) -> false でした。
- tree[6] を 参照します。
- tree[6]: [4, 5, 7] のうち、未探索の [5, 7] を stack に push します。
4回目の探索
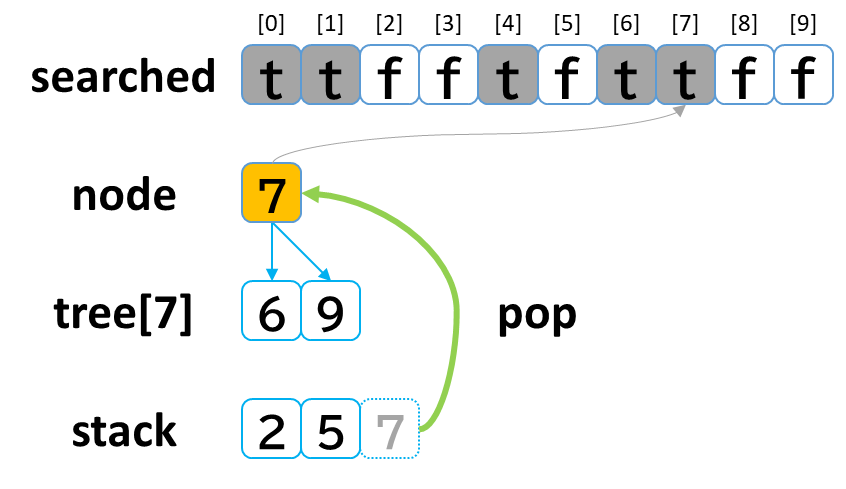
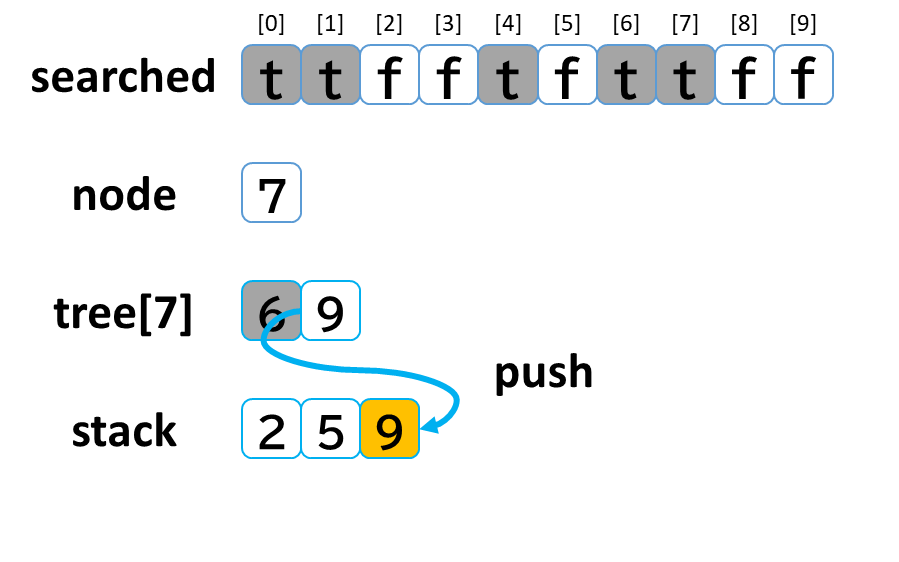
- stack から pop して node に代入します。(node = 7)
- searched[7] を true にします。
- node (7) == treasure (8) -> false でした。
- tree[7] を 参照します。
- tree[7]: [6, 9] のうち、未探索の [9] を stack に push します。
5回目の探索
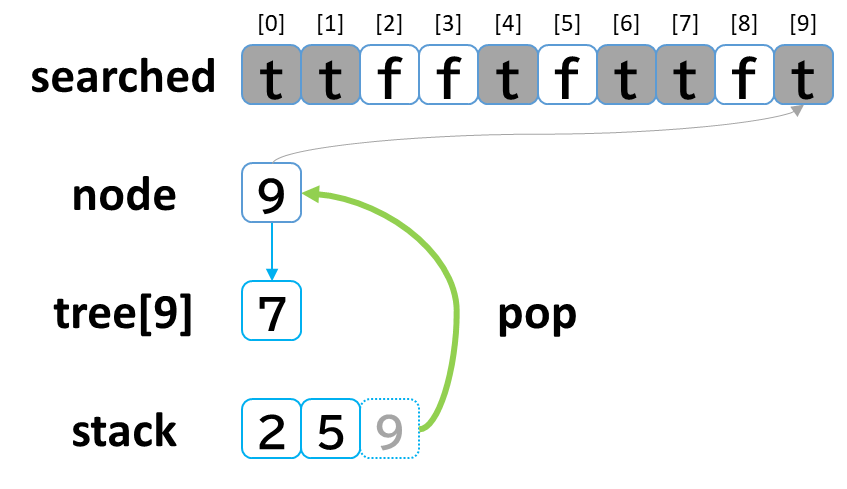

- stack から pop して node に代入します。(node = 9)
- searched[9] を true にします。
- node (9) == treasure (8) -> false でした。
- tree[9] を 参照します。
- tree[9]: [7] のうち、未探索はありませんでした。
(行き止まりまで探索しました。)
6回目の探索
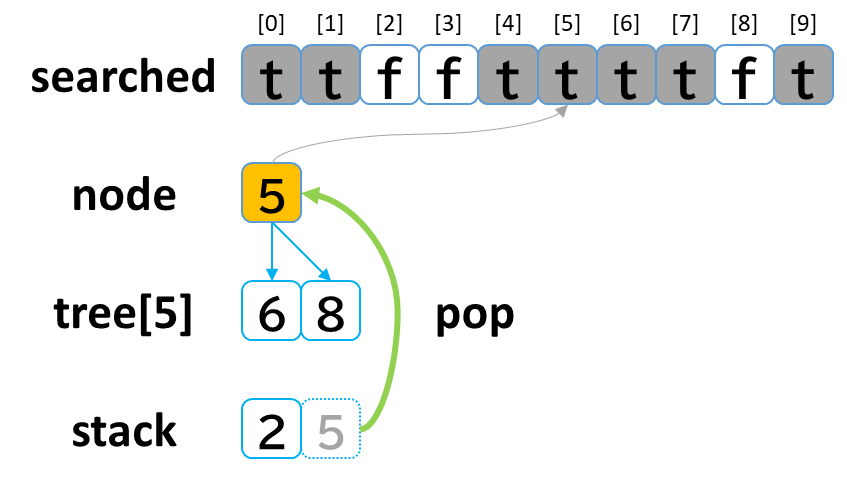
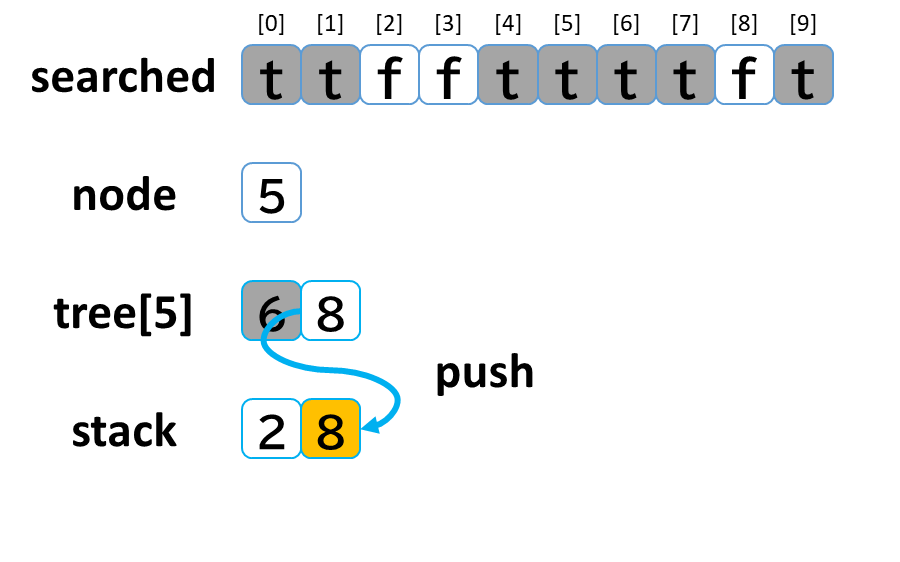
- stack から pop して node に代入します。(node = 5)
- searched[5] を true にします。
- node (5) == treasure (8) -> false でした。
- tree[5] を 参照します。
- tree[5]: [6, 8] のうち、未探索の [8] を stack に push します。
7回目の探索
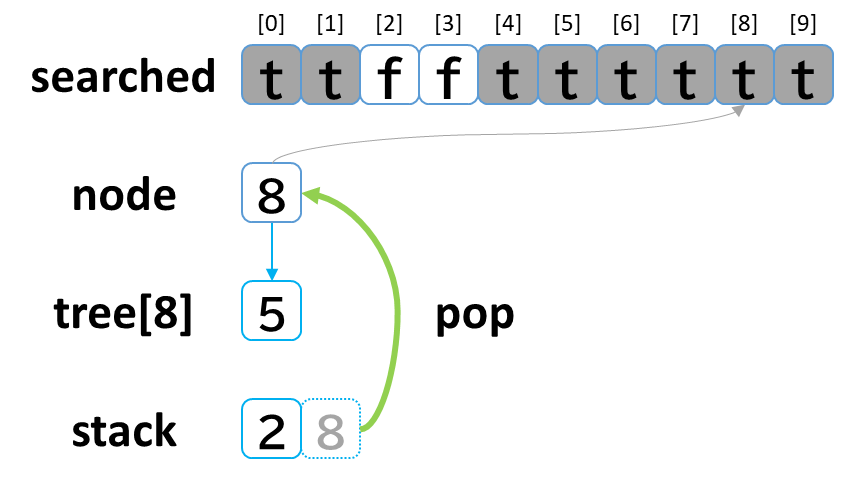
- stack から pop して node に代入します。(node = 8)
- searched[8] を true にします。
- node (8) == treasure (8) -> true でした。(お宝発見!)
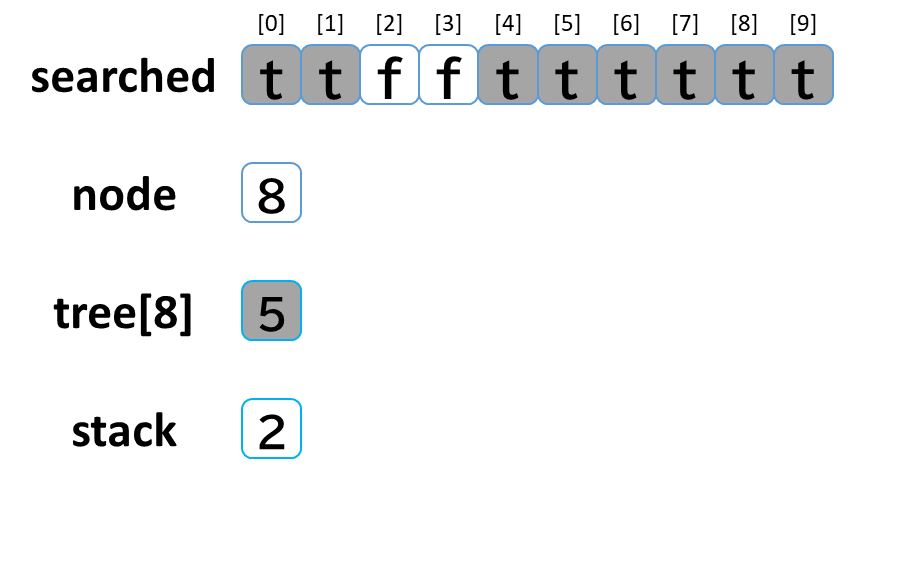
- tree[8] を 参照します。
- tree[8]: [5] のうち、未探索はありませんでした。
(行き止まりまで探索しました。)
8回目の探索
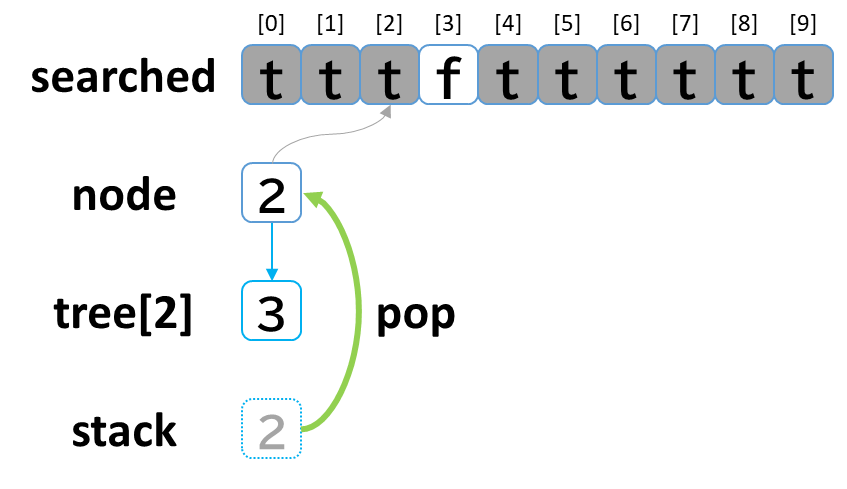
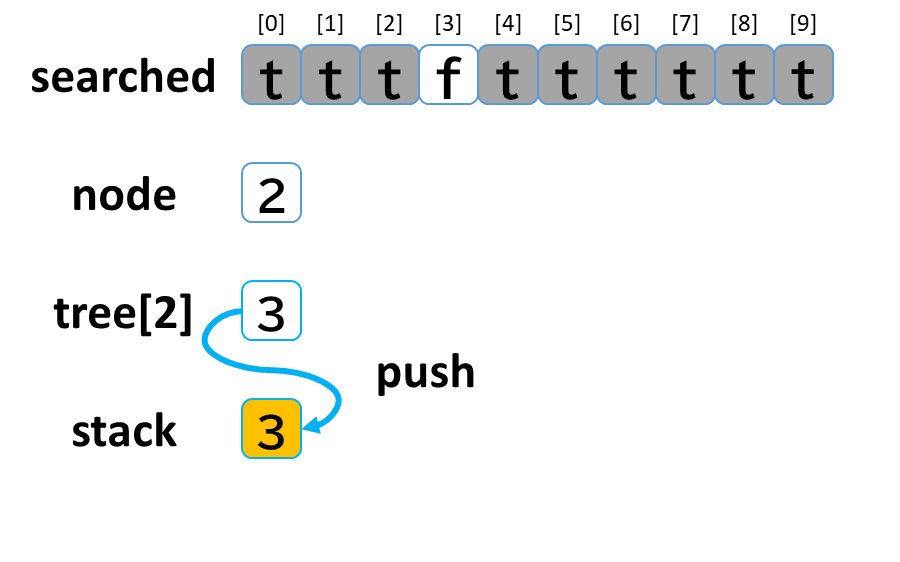
- stack から pop して node に代入します。(node = 2)
- searched[2] を true にします。
- node (2) == treasure (8) -> false でした。
- tree[2] を 参照します。
- tree[2]: [3] のうち、未探索の [3] を stack に push します。
9回目の探索
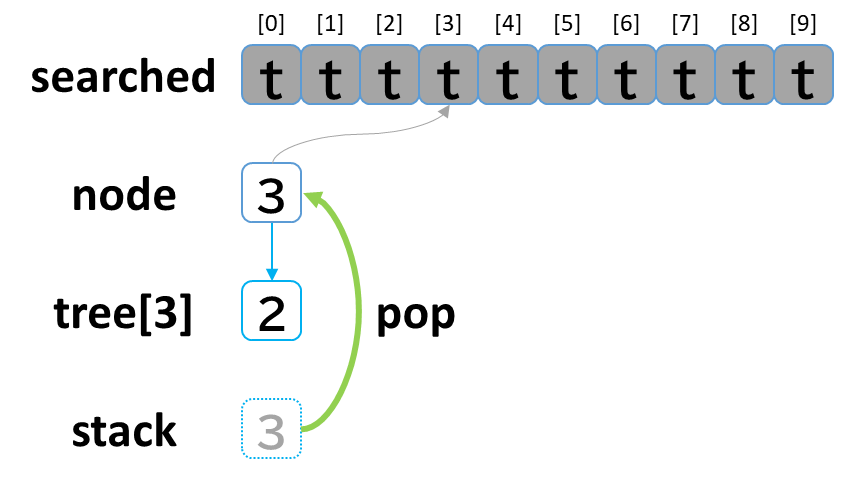

- stack から pop して node に代入します。(node = 3)
- searched[3] を true にします。
- node (3) == treasure (8) -> false でした。
- tree[3] を 参照します。
- tree[3]: [2] のうち、未探索はありませんでした。
(行き止まりまで探索しました。)
stack が空になったので繰り返し処理を終了します。
幅優先探索(Breadth First Search)
探索開始地点から隣接するノードを探索し、同じ深さのノードの探索が終わってから次の深さの探索を繰り返します。
実装例
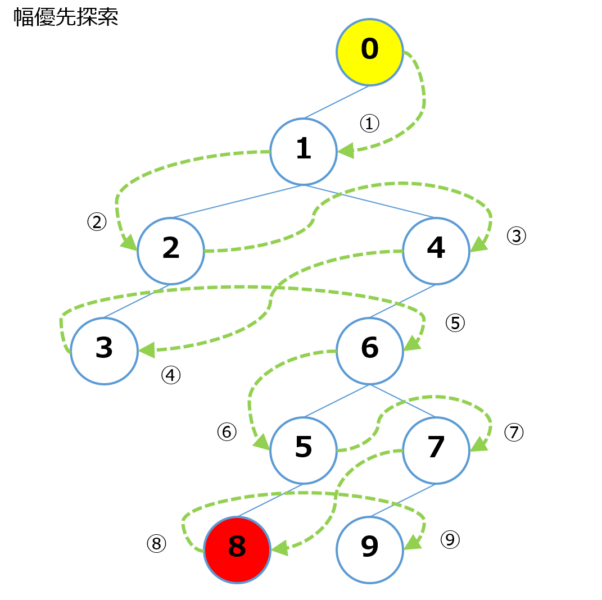
下図の木構造の [0] から幅優先探索を行い、 [8] にあるお宝を探索する様子をシミュレーションしてみます。
データ構造
サンプルコード
# スタート位置の設定
start = 0
# お宝の位置の設定 (treasure ≠ start)
treasure = 8
# 要素の繋がり設定
tree = [[1], # [0] は [1] と隣接
[0, 2, 4], # [1] は [0, 2, 4] と隣接
[1, 3], # [2] は [1, 3] と隣接
[2], # [3] は [2] と隣接
[1, 6], # [4] は [1, 6] と隣接
[6, 8], # [5] は [6, 8] と隣接
[4, 5, 7], # [6] は [4, 5, 7] と隣接
[6, 9], # [7] は [6, 9] と隣接
[5], # [8] は [5] と隣接
[7]] # [9] は [7] と隣接
# 探索済みチェック用
searched = Array.new(tree.length, false)
# スタート位置の設定
searched[start] = true
queue = tree[start]
step = 0
# 幅優先探索
while queue.length > 0
step += 1
puts <<~"EOS"
--------------------
#{step}
探索候補 -> #{queue}
EOS
# 配列先頭から要素を取り出す
node = queue.shift
searched[node] = true
msg = "tree[#{node}] を探索 -> "
if node == treasure
puts msg << "お宝発見!"
# break
else
puts msg << "お宝はありませんでした"
end
puts "探索済みリスト -> #{searched}"
# 隣接ノードのうち未探索を探索候補に入れる
next_nodes = tree[node].select { |node| not searched[node] }
puts "追加候補 -> #{next_nodes}"
next_nodes.each { |node| queue.push(node) }
end
処理の流れ
繰り返し処理に入る前にスタート位置 (0) の設定を行います。
(start ≠ treasure とします)
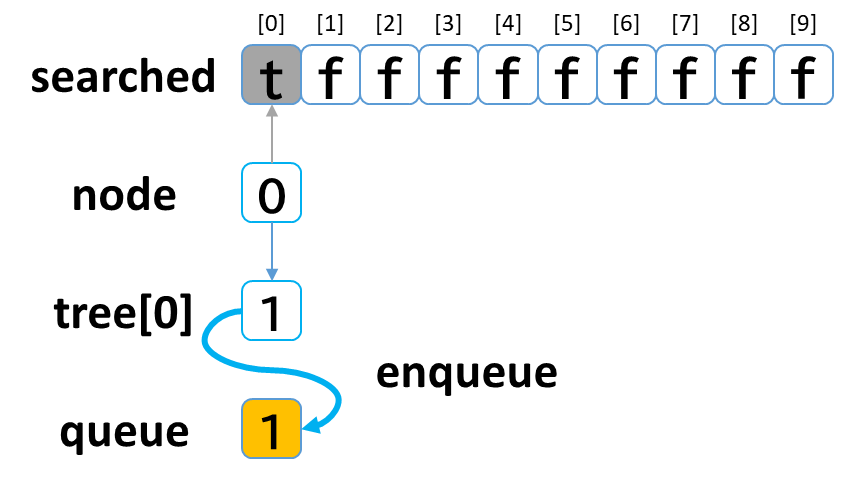
- searched[0] を true にします。
(node[0] を探索済みにします。) - tree[0](node[0]の隣接ノード)を先頭から全て queue に enqueue します。
(初回なのでnode[0]の隣接ノードは未探索です。)
ここから繰り返し処理です。queue が空になるまで繰り返します。
1回目の探索
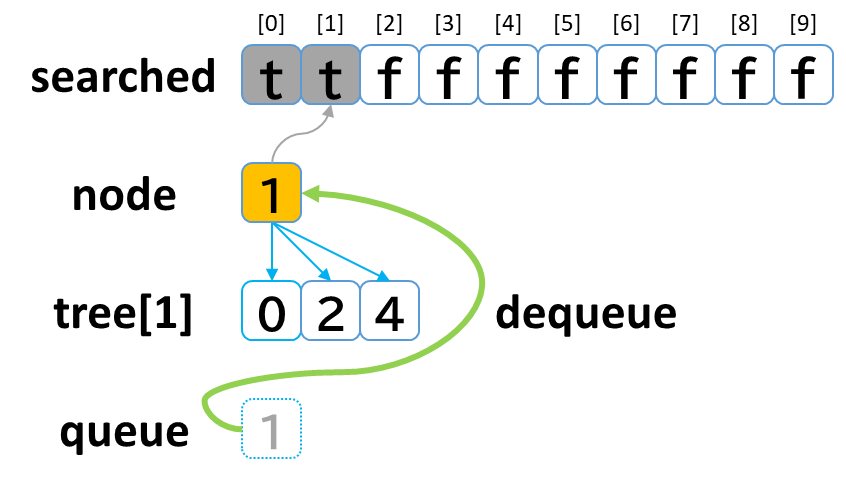
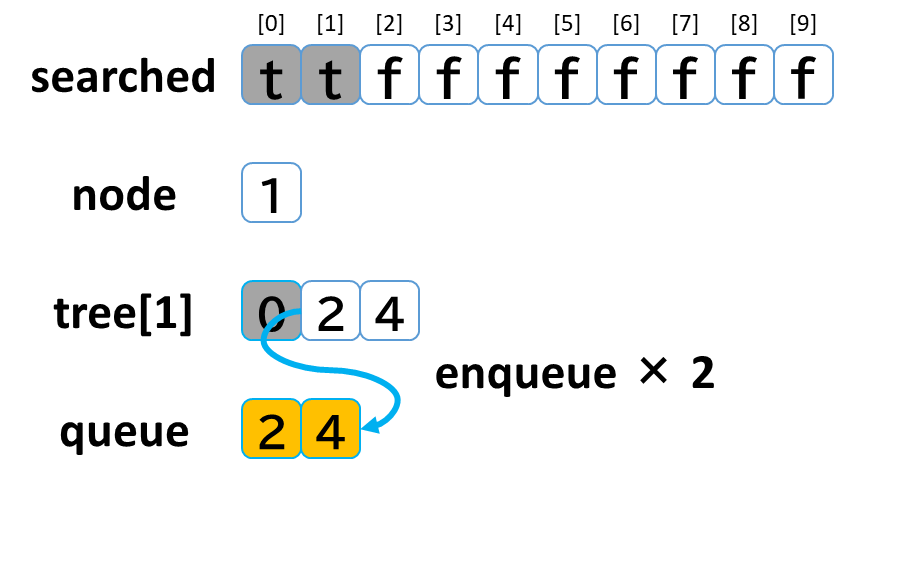
- queue から dequeue して node に代入します。(node = 1)
- searched[1] を true にします。
- node (1) == treasure (8) -> false でした。
- tree[1] を 参照します。
- tree[1]: [0, 2, 4] のうち、未探索の [2, 4] を queue に enqueue します。
2回目の探索
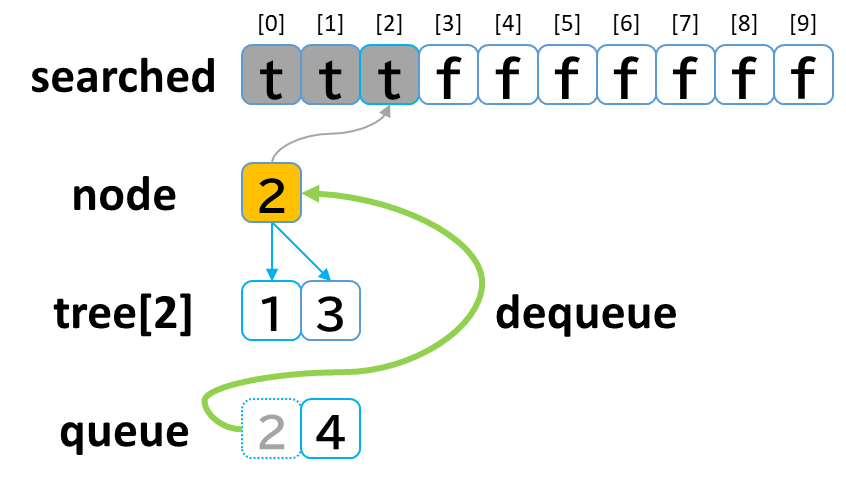
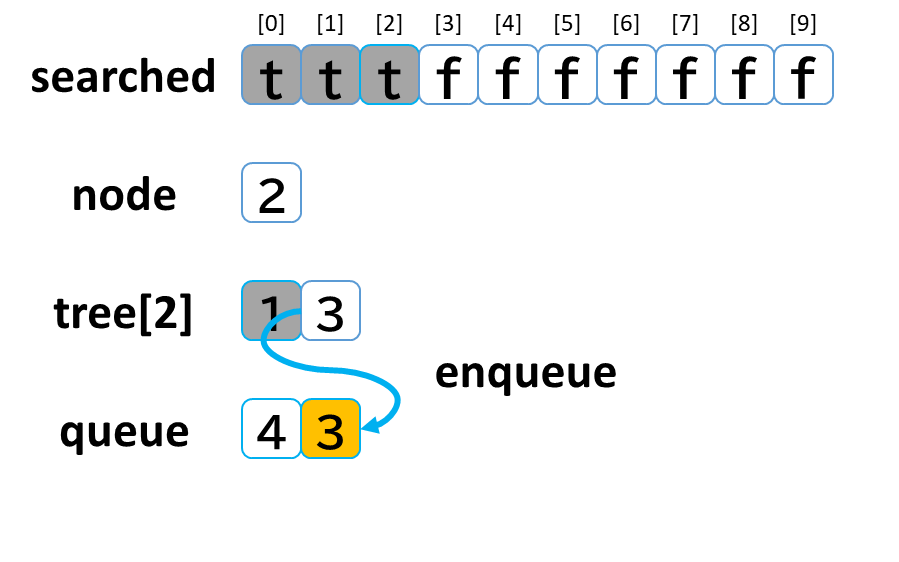
- queue から dequeue して node に代入します。(node = 2)
- searched[2] を true にします。
- node (2) == treasure (8) -> false でした。
- tree[2] を 参照します。
- tree[2]: [1, 3] のうち、未探索の [3] を queue に enqueue します。
3回目の探索
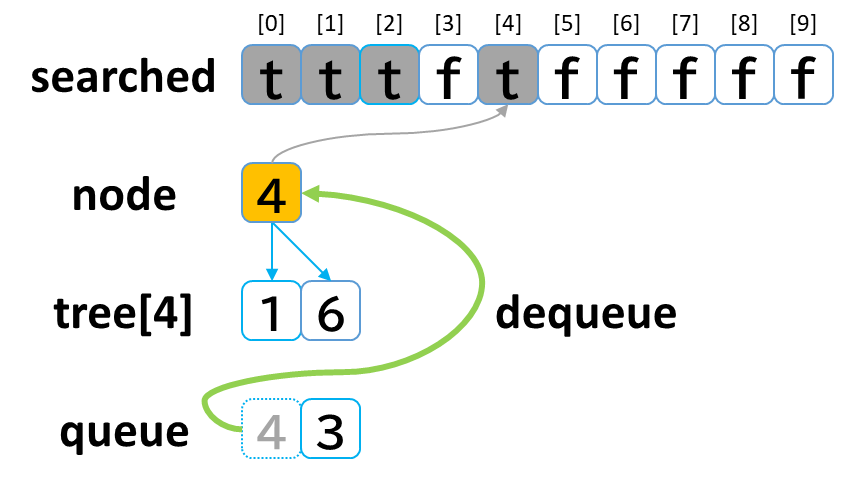
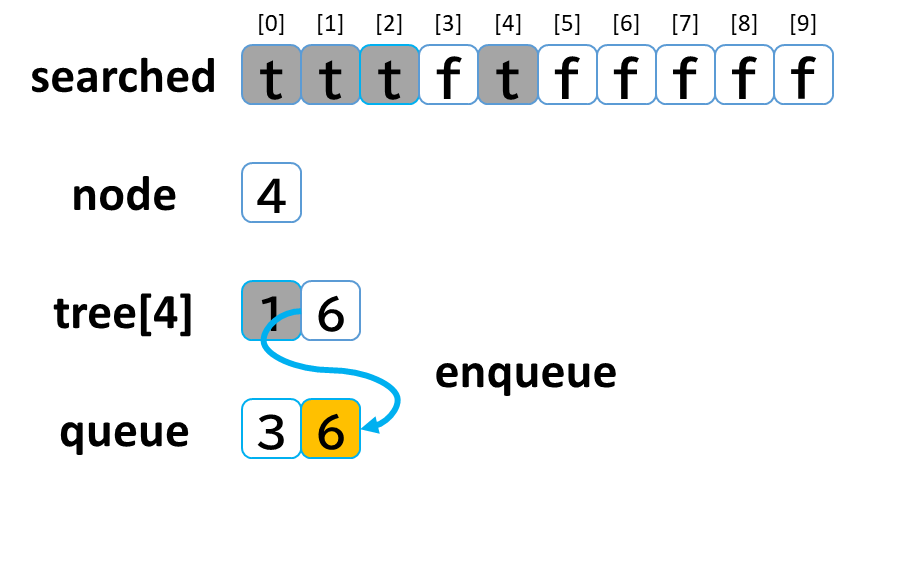
- queue から dequeue して node に代入します。(node = 4)
- searched[4] を true にします。
- node (4) == treasure (8) -> false でした。
- tree[4] を 参照します。
- tree[4]: [1, 6] のうち、未探索の [6] を queue に enqueue します。
4回目の探索
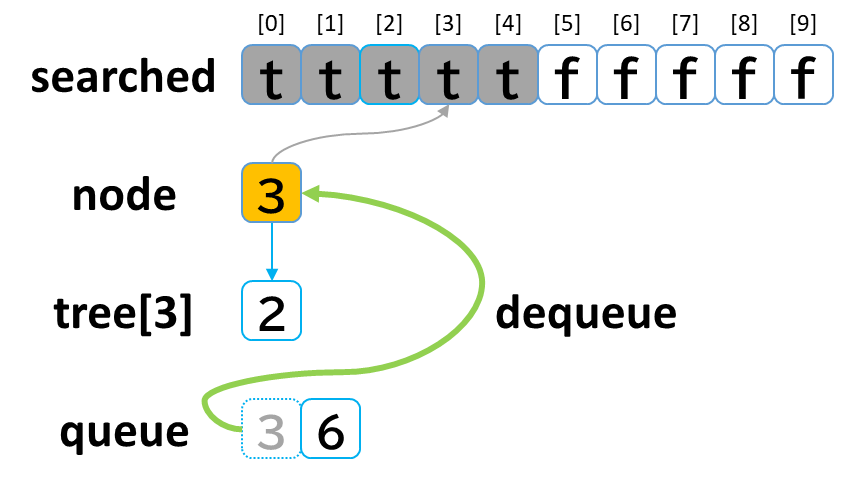
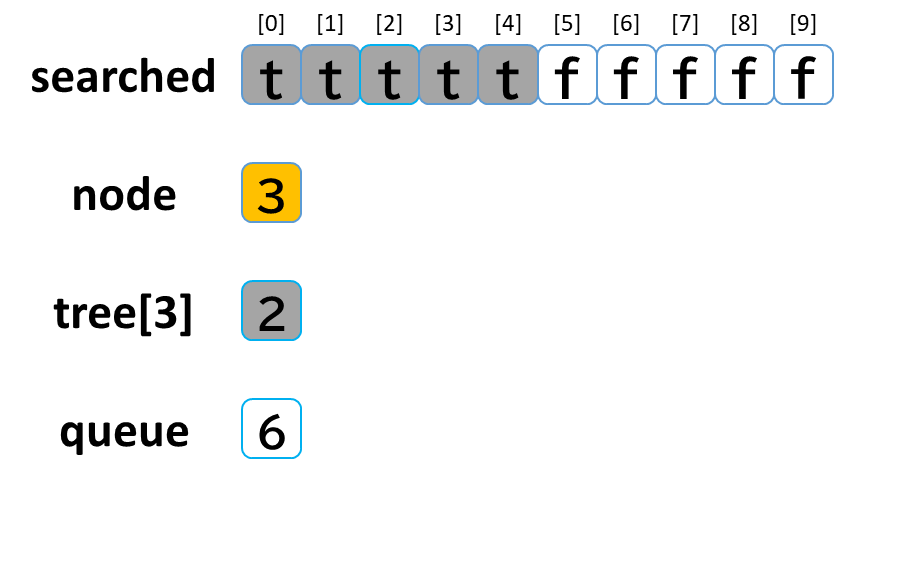
- queue から dequeue して node に代入します。(node = 3)
- searched[3] を true にします。
- node (3) == treasure (8) -> false でした。
- tree[3] を 参照します。
- tree[3]: [2] のうち、未探索はありませんでした。
(行き止まりまで探索しました。)
5回目の探索
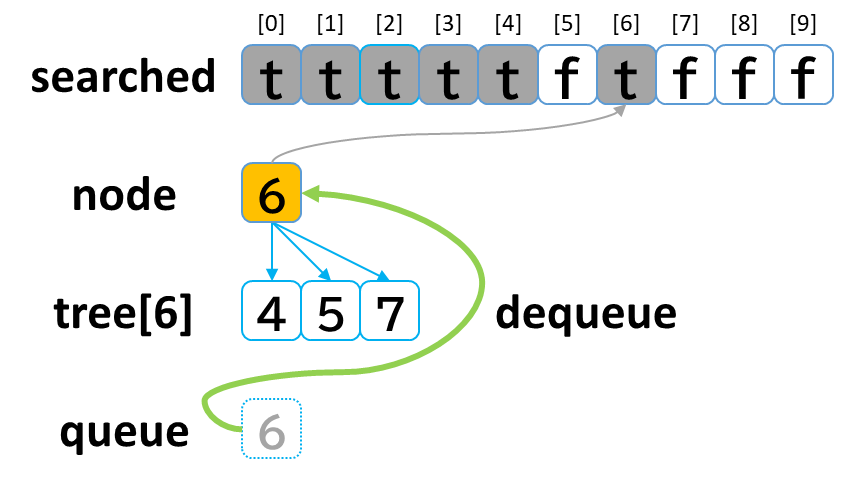
- queue から dequeue して node に代入します。(node = 6)
- searched[6] を true にします。
- node (6) == treasure (8) -> false でした。
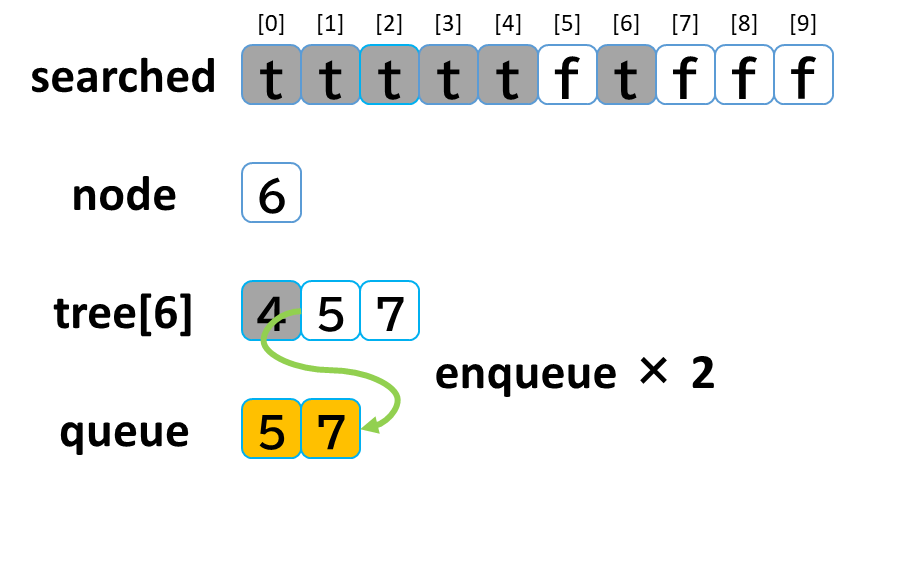
- tree[6] を 参照します。
- tree[6]: [4, 5, 7] のうち、未探索の [5, 7] を queue に enqueue します。
6回目の探索
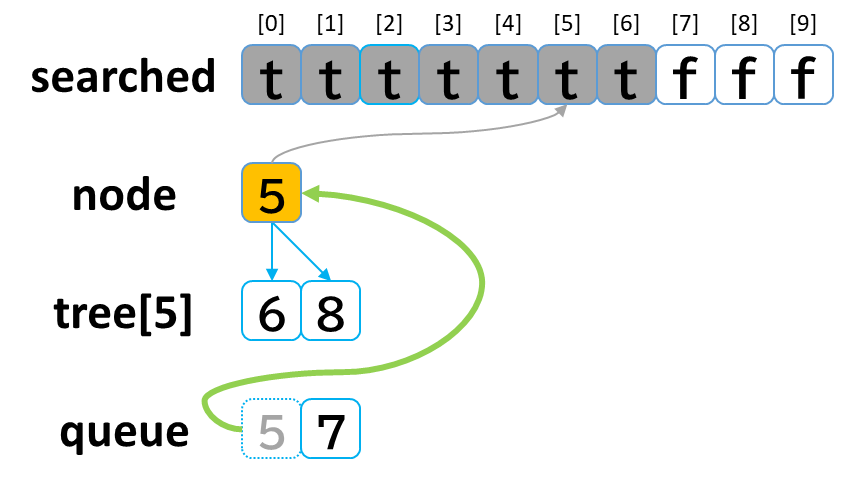
- queue から dequeue して node に代入します。(node = 5)
- searched[5] を true にします。
- node (5) == treasure (8) -> false でした。
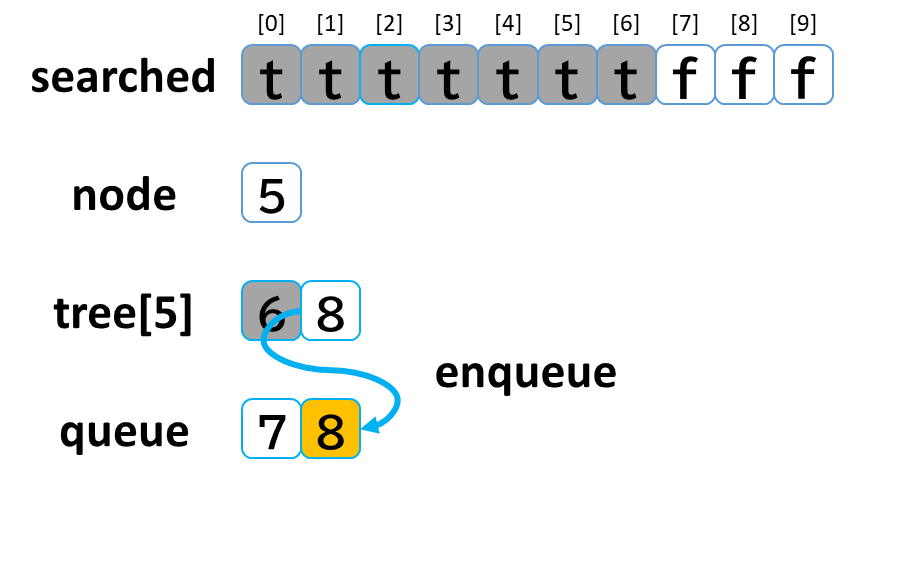
- tree[5] を 参照します。
- tree[5]: [6, 8] のうち、未探索の [8] を queue に enqueue します。
7回目の探索
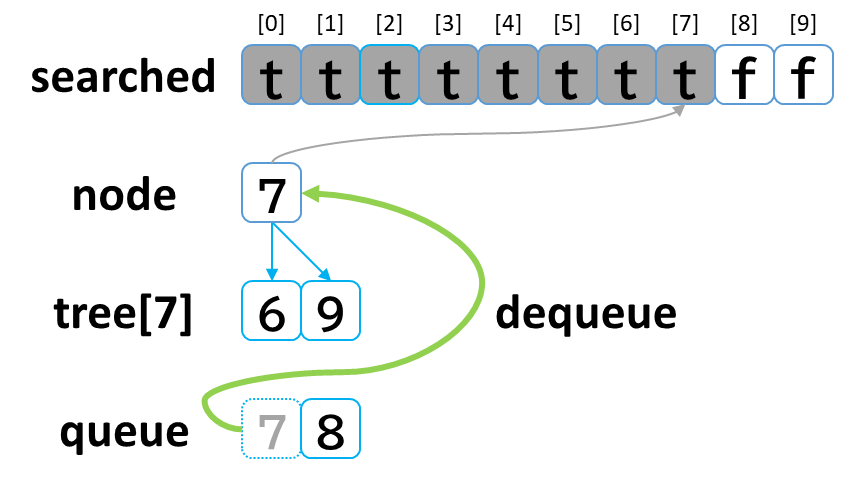
- queue から dequeue して node に代入します。(node = 7)
- searched[7] を true にします。
- node (7) == treasure (8) -> false でした。
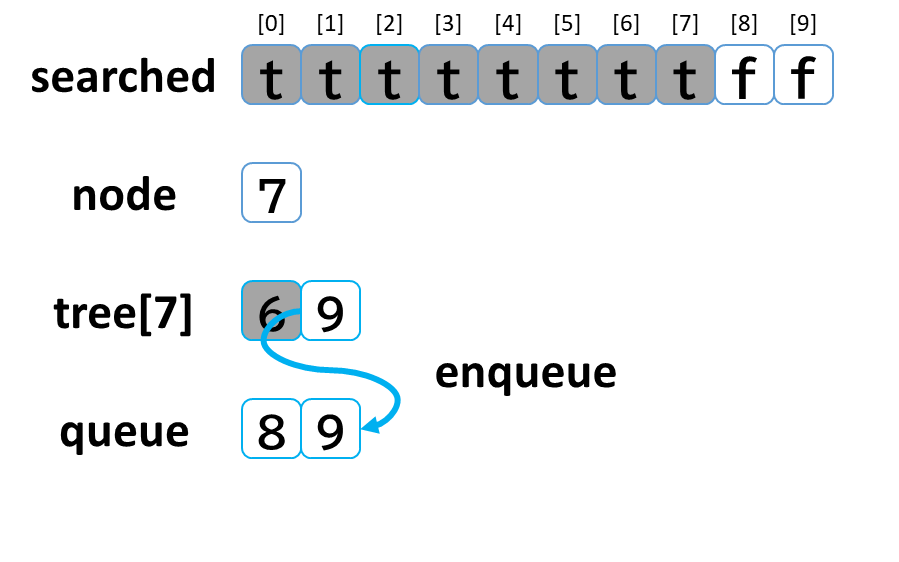
- tree[7] を 参照します。
- tree[7]: [6, 9] のうち、未探索の [9] を queue に enqueue します。
8回目の探索
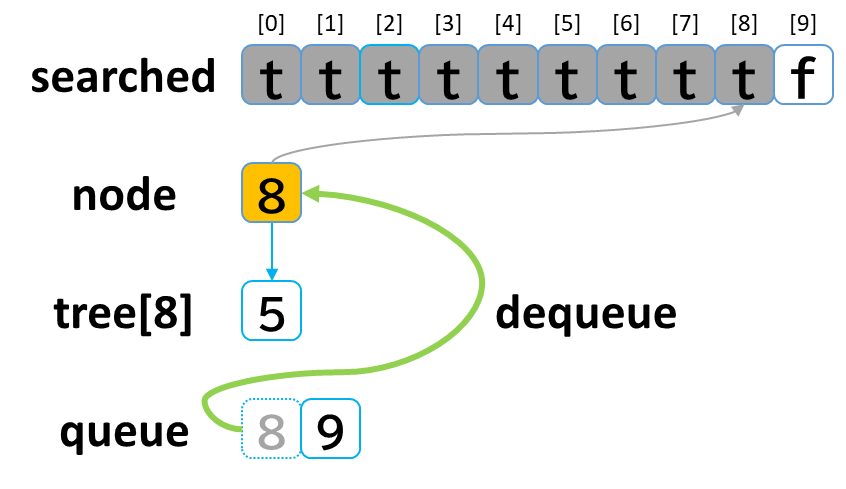
- queue から dequeue して node に代入します。(node = 8)
- searched[8] を true にします。
- node (8) == treasure (8) -> true でした。(お宝発見!)
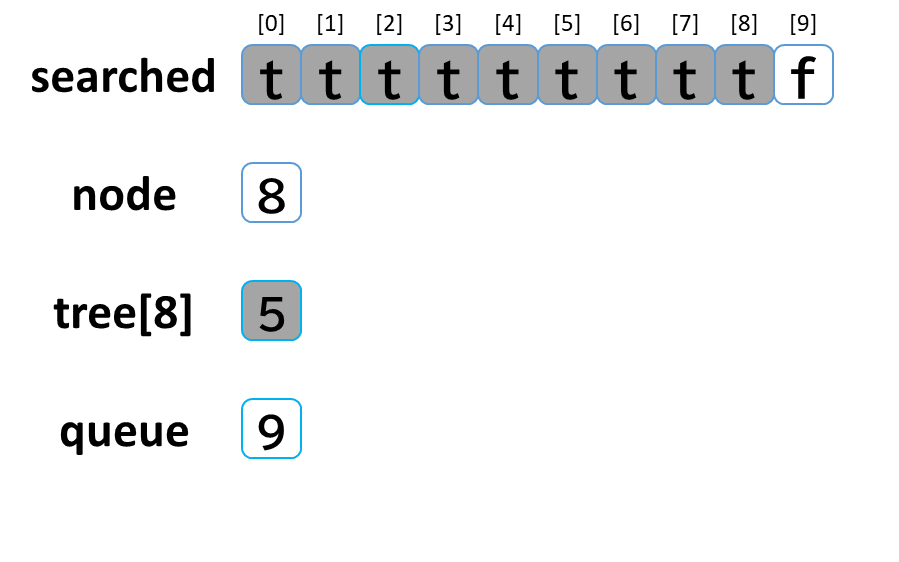
- tree[8] を 参照します。
- tree[8]: [5] のうち、未探索はありませんでした。
(行き止まりまで探索しました。)
9回目の探索
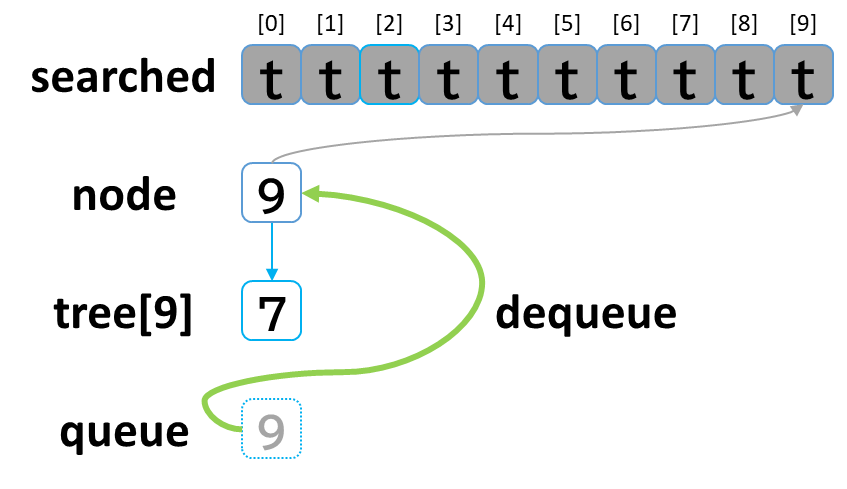
- queue から dequeue して node に代入します。(node = 9)
- searched[9] を true にします。
- node (9) == treasure (8) -> false でした。
- tree[9] を 参照します。
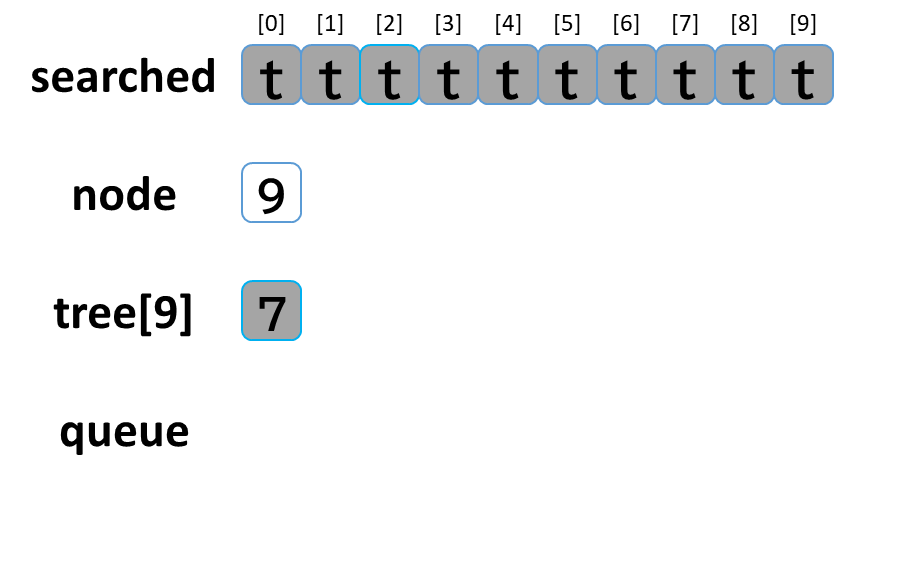
- tree[9]: [7] のうち、未探索はありませんでした。
(行き止まりまで探索しました。)
queue が空になったので繰り返し処理を終了します。
今回のまとめ
- 深さ優先探索(Depth First Search)、幅優先探索(Breadth First Search)は全探索の一種です。
- スタックを使うと深さ優先探索、キューを使うと幅優先探索が実装出来ます。
- 深さ優先探索は一つの分岐を調べ終わってから次の分岐を探索します。
- 幅優先探索は開始位置から近い順に探索します。
- 良い実装をするためには探索対象によってアルゴリズムを選択する必要があります。

深さ優先探索・幅優先探索を覚えると競プロの色々な問題が解けるようになります。
paiza練習問題集にも深さ優先探索・幅優先探索メニューがありますので、ぜひ挑戦してみて下さい!




