[アルゴリズム(Ruby)]ダイクストラ法の解説

ダイクストラ法(Dijkstra's Algorithm)

ダイクストラ法は、グラフ上のある点から、ある点までの最短経路を求めるアルゴリズムで、コストに負数が含まれない時に使用できます。

例えば、カーナビで現在地から目的地までの最短経路を検索するような動作を実装することができます。

ノード（地点）の繋がりをグラフで表す

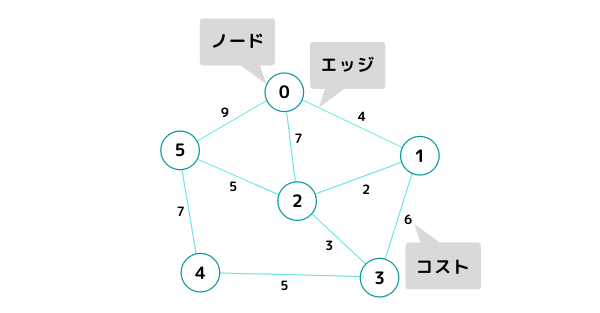
地点と地点やモノとモノの繋がり（ネットワーク）を表した図をグラフといい、点をノード（節）、点同士を繋ぐ線をエッジ（辺）、距離をコスト（重み）と言います。

例えば下図でノード0とノード1はコスト4で行ったり来たり出来ることを表しています。（無向グラフ）
また、エッジを矢印にすることで一方通行を表現することもできます。（有向グラフ）

グラフを表すデータ構造

プログラミングでグラフを表すデータ構造として、隣接行列と隣接リストがあります。
上図グラフの繋がりは以下のデータ構造で表現することが出来ます。

隣接行列

# 隣接行列
adjacency_matrix = [
  [nil,   4,   7, nil, nil,   9],
  [  4, nil,   2,   6, nil, nil],
  [  7,   2, nil,   3, nil,   5],
  [nil,   6,   3, nil,   5, nil],
  [nil, nil, nil,   5, nil,   7],
  [  9, nil,   5, nil,   7, nil]
]

隣接リスト

# 隣接リスト
adjacency_list = [
  [[1, 4], [2, 7], [5, 9]],
  [[0, 4], [2, 2], [3, 6]],
  [[0, 7], [1, 2], [3, 3], [5, 5]],
  [[1, 6], [2, 3], [4, 5]],
  [[3, 5], [5, 7]],
  [[0, 9], [4, 7]]
]

アルゴリズム解説

ダイクストラ法のアルゴリズムについて解説します。
今回はグラフの繋がりを表すデータ構造に隣接リストを使います。

処理の流れ

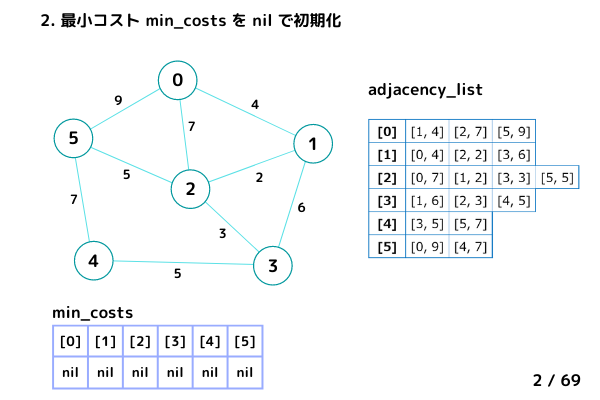
1. グラフの隣接リストadjacency_listを定義する
2. 各ノードまでの最小コストmin_costsを取り得ない値で初期化する
   (今回は nil とします)
3.  探索リストsearch_listに[初期コスト, 開始ノード番号]を追加する (※注)
4. search_listに要素がある間実行するループを設定する
   1. search_listから最小コストの要素[cost, node]を取り出す
   2. 取り出したノードの最小コストmin_costs[node]が確定済みならループをスキップする
   3. 取り出したノードの最小コストmin_costs[node]を確定する
   4. 全ノードの最小コストが確定したらループを終了する
   5. 隣接ノード[next_cost, next_node]を順番に参照する
      1. 隣接ノードの最小コストmin_costs[next_node]が確定済みならループをスキップする
      2. search_listに隣接ノードまでのコストとノード番号[cost+next_cost, next_node]を追加する
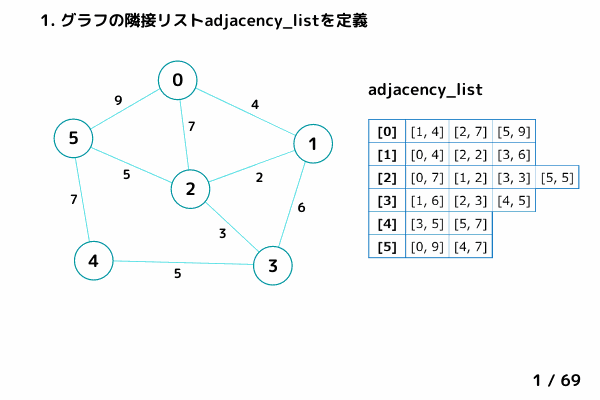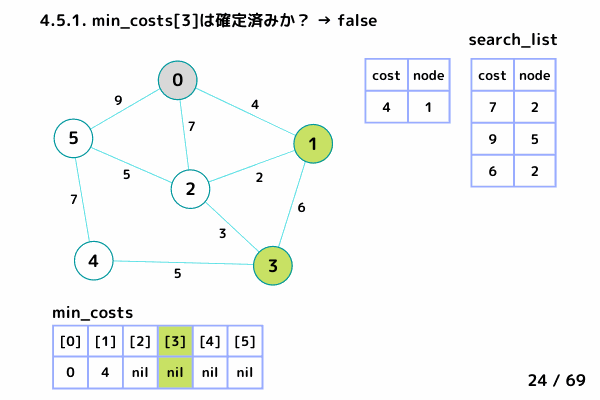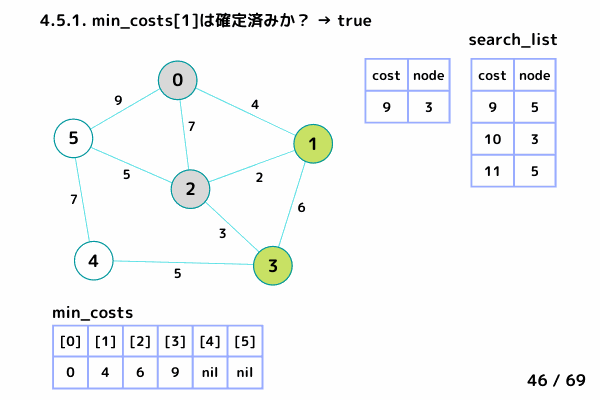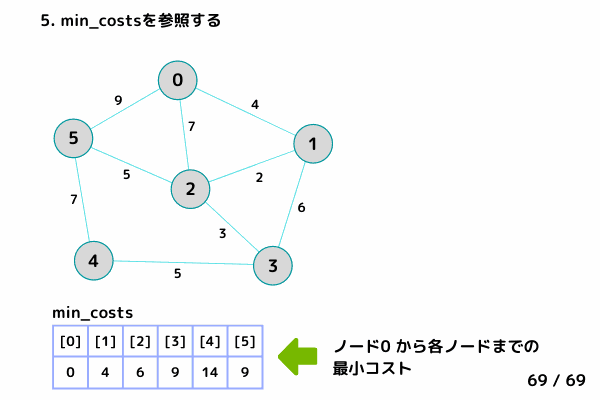
5. min_costsを参照する(各ノードまでの最小コストが格納されている)

サンプルコード（全体）

# ダイクストラ法(Dijkstra's Algorithm)

require "./priority_queue"

# ----------------------------------
# 1. グラフの隣接リストadjacency_listを定義
# ----------------------------------
ADJACENCY_LIST = [
  [[1, 4], [2, 7], [5, 9]],
  [[0, 4], [2, 2], [3, 6]],
  [[0, 7], [1, 2], [3, 3], [5, 5]],
  [[1, 6], [2, 3], [4, 5]],
  [[3, 5], [5, 7]],
  [[0, 9], [4, 7]],
]
# NODE: ノード数, START: 開始ノード番号
NODE = 6
START = 0

# ----------------------------------
# 2. 最小コスト min_costs を nil で初期化
# ----------------------------------
min_costs = Array.new(NODE)

# ----------------------------------
# 3. 探索リストserch_listに
# [初期コスト, 開始ノード番号]を追加
# ----------------------------------
search_list = PriorityQueue.new
search_list.insert([0, 0])

# ----------------------------------
# 4. search_listに要素がある間繰り返す
# ----------------------------------
while search_list.size > 0

  # ----------------------------------
  # 4.1. 最小コストの要素[cost, node]を取り出す
  # ----------------------------------
  cost, node = search_list.extract

  # ----------------------------------
  # 4.2. min_costs[node]が確定済みならスキップ
  # ----------------------------------
  next if not min_costs[node].nil?

  # ----------------------------------
  # 4.3. 取り出したノードの最小コストを確定
  # ----------------------------------
  min_costs[node] = cost

  # ----------------------------------
  # 4.4. 全ノードの最小コストが確定したら終了
  # ----------------------------------
  break if not min_costs.any?(nil)

  # ----------------------------------
  # 4.5. 隣接ノードを順番に参照する
  # ----------------------------------
  ADJACENCY_LIST[node].each do |next_node, next_cost|
    # ----------------------------------
    # 4.5.1. 隣接ノードの最小コストが確定済みならスキップ
    # ----------------------------------
    next if not min_costs[next_node].nil?

    # ----------------------------------
    # 4.5.2. search_listに隣接ノードまでの
    # コストとノード番号[cost + next_cost, next_node]を追加
    # ----------------------------------
    search_list.insert([cost + next_cost, next_node])
  end
end

# ----------------------------------
# 5. min_costsを参照する
# ----------------------------------
min_costs.each_with_index do |cost, idx|
  puts "#{START} から #{idx} までの最小コストは #{cost.to_s.rjust(2)} です"
end

# 実行結果
# > 0 から 0 までの最小コストは  0 です
# > 0 から 1 までの最小コストは  4 です
# > 0 から 2 までの最小コストは  6 です
# > 0 から 3 までの最小コストは  9 です
# > 0 から 4 までの最小コストは 14 です
# > 0 から 5 までの最小コストは  9 です

処理の流れ（全体）

処理の流れ（パート別）

初期設定 (1/69 ～ 3/69)

1. グラフの隣接リストadjacency_listを定義する

2. 最小コストmin_costsをnilで初期化する

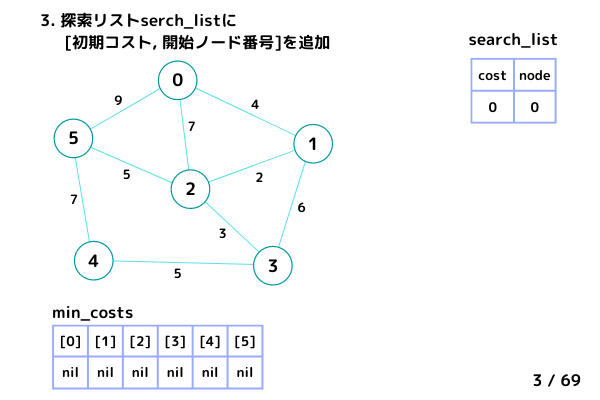
3. 探索リストsearch_listに [初期コスト, 開始ノード番号] を追加

初期コスト 0 として、ノード 0 から探索を開始する。

search_list に要素がある間繰り返すループ

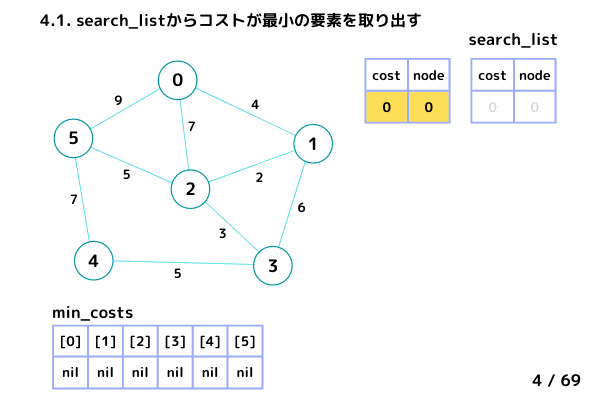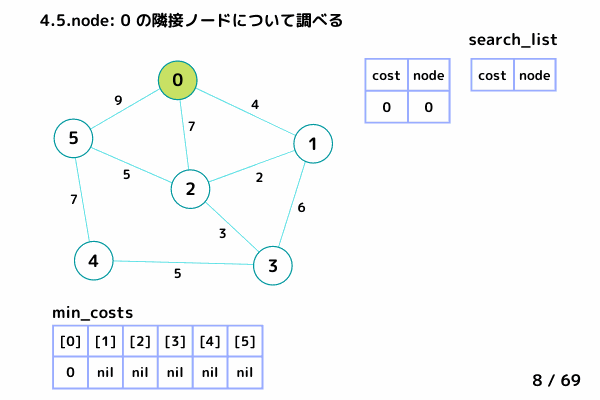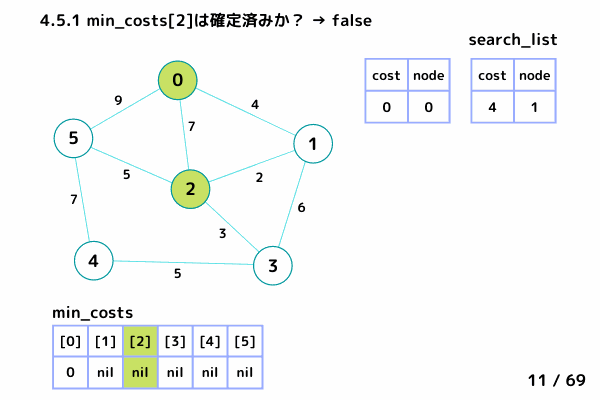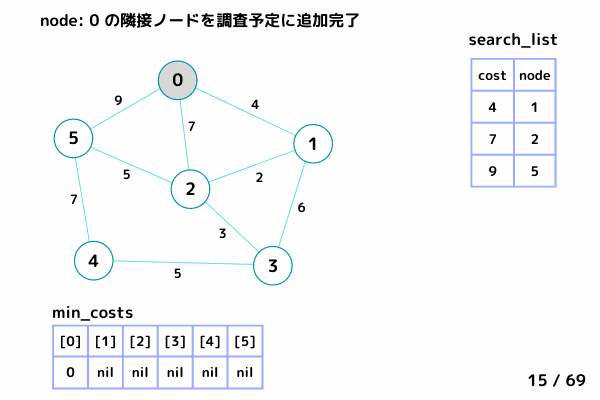
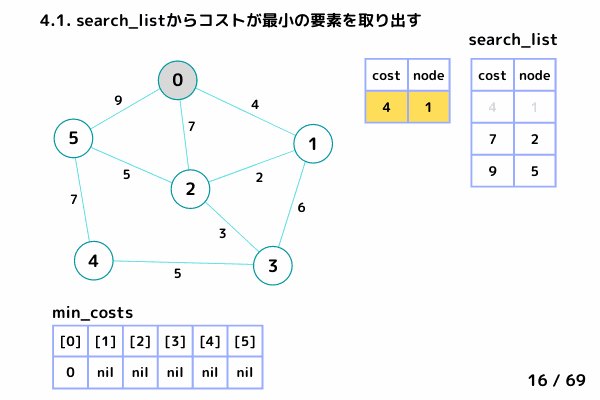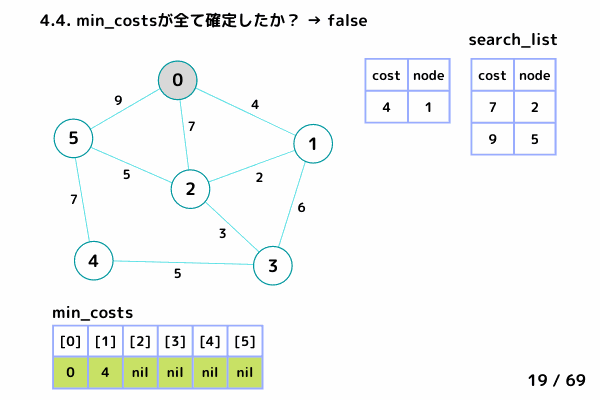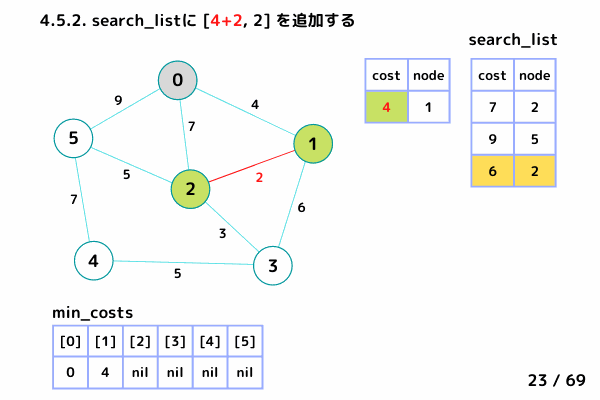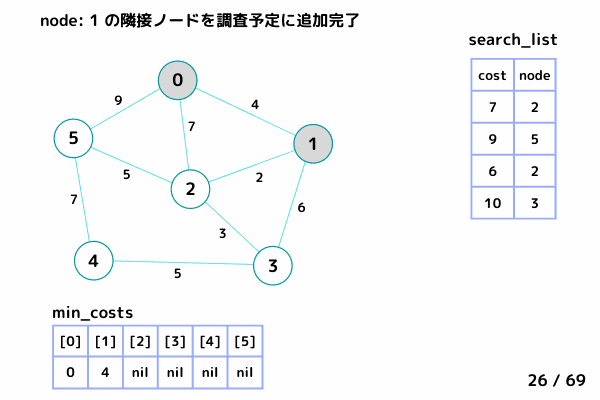
ノード0の処理 (4/69 ～ 15/69)

4.1. 最小コストの要素[cost, node]を取り出す → [cost = 0, node= 0]

4.2. min_costs[0]: false → スキップしない

4.3. min_costs[0] = 0 → ノード0 の最小コストを 0 で確定

4.4. min_costsが全て確定したか？: false → 終了しない

4.5. ノード0 の隣接ノードを参照
　→ ノード1: [0+4, 1], ノード2: [0+7, 2], ノード5: [0+9, 5] を search_list に追加

ノード1の処理 (16/69 ～ 26/69)

4.1. 最小コストの要素[cost, node]を取り出す→ [cost = 4, node= 1]

4.2. min_costs[1]: false → スキップしない

4.3. min_costs[1] = 4 → ノード1 の最小コストを 4 で確定

4.4. min_costsが全て確定したか？: false → 終了しない

4.5. ノード1 の隣接ノードを参照
ノード0 は確定済みなのでスキップ
ノード2: [4+2, 2], ノード3: [4+6, 3] を search_list に追加

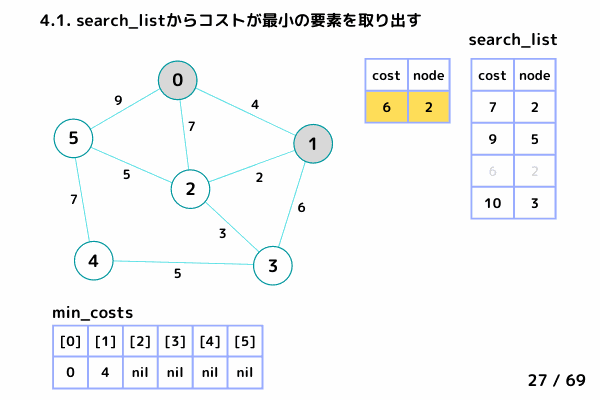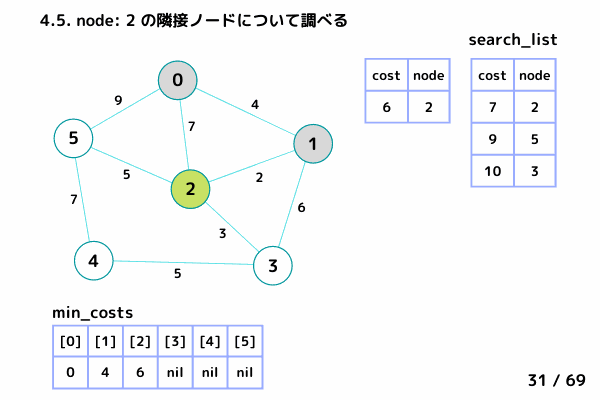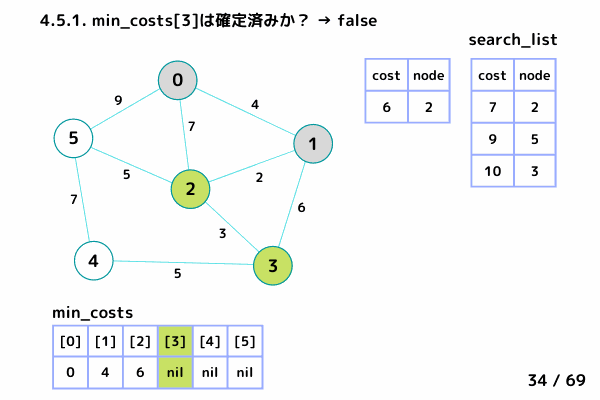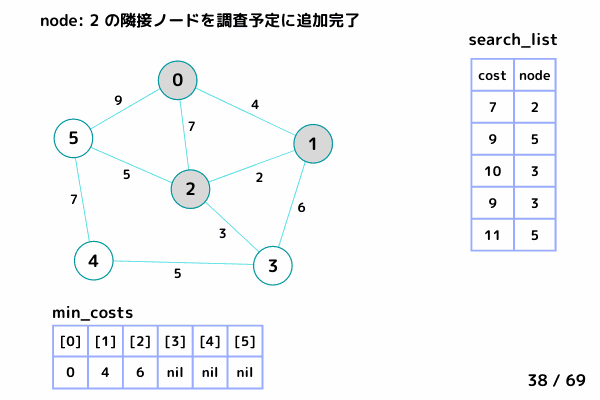
ノード2の処理 (27/69 ～ 38/69)

4.1. 最小コストの要素[cost, node]を取り出す → [cost = 6, node= 2]

4.2. min_costs[2]: false → スキップしない

4.3. min_costs[2] = 6 → ノード2 の最小コストを 6 で確定

4.4. min_costsが全て確定したか？: false → 終了しない

4.5. ノード2 の隣接ノードを参照
→ ノード0, ノード1 は確定済みなのでスキップ
→ ノード3: [6+3, 3], ノード5: [6+5, 5] を search_list に追加

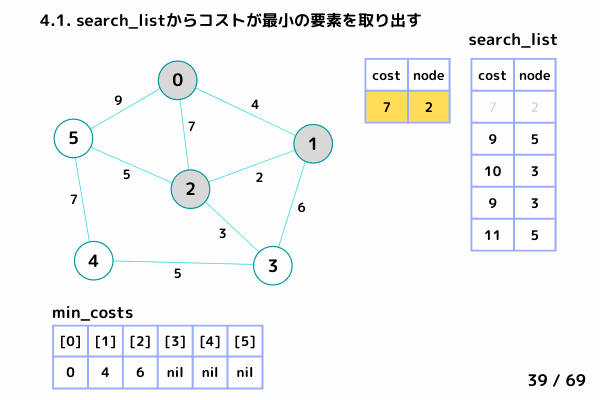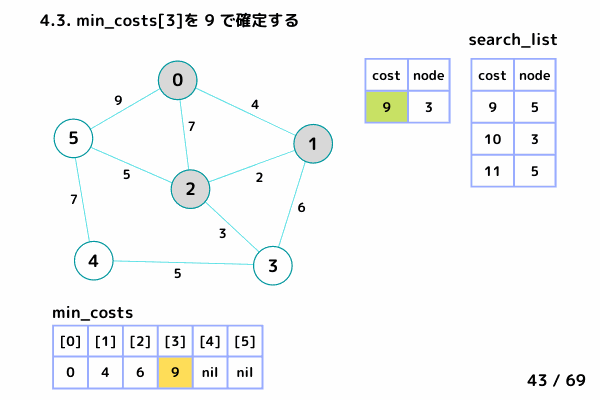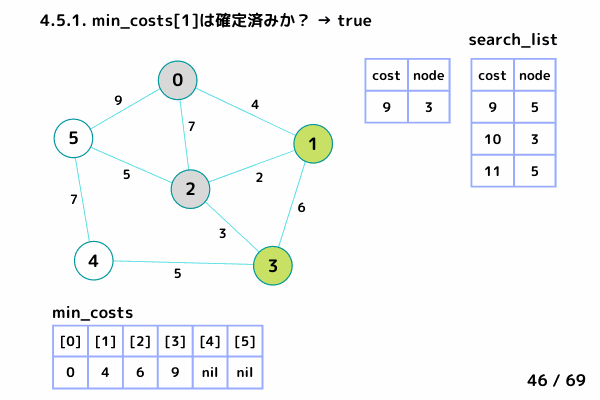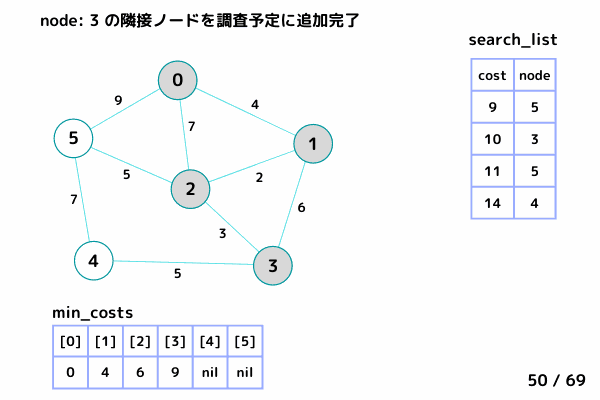
ノード3の処理 (39/69 ～ 50/69)

4.1. 最小コストの要素[cost, node]を取り出す
→ [cost = 7, node= 2] は確定済みなのでスキップ
→ [cost = 9, node= 3]

4.2. min_costs[3]: false → スキップしない

4.3. min_costs[3] = 9 → ノード3 の最小コストを 9 で確定

4.4. min_costsが全て確定したか？: false → 終了しない

4.5. ノード3 の隣接ノードを参照
ノード1, ノード2 は確定済みなのでスキップ
ノード4: [9+5, 4] を search_list に追加

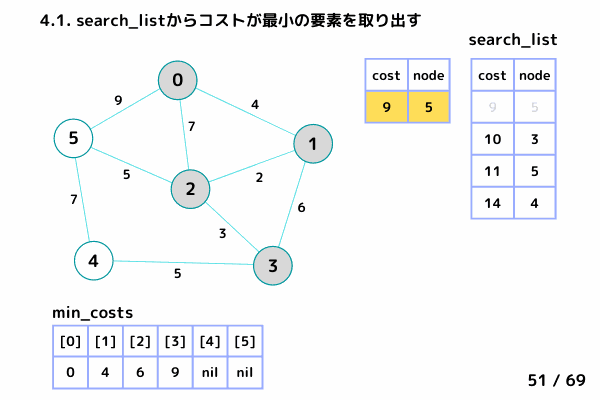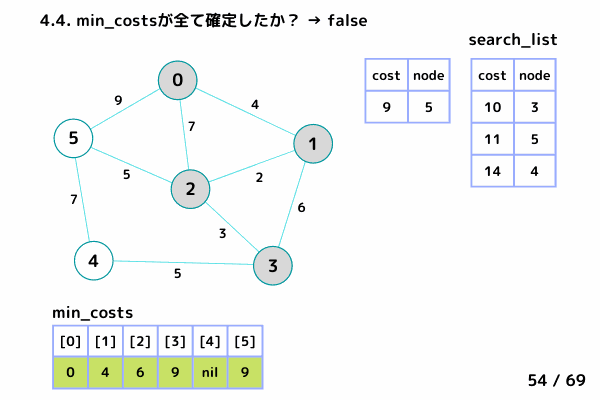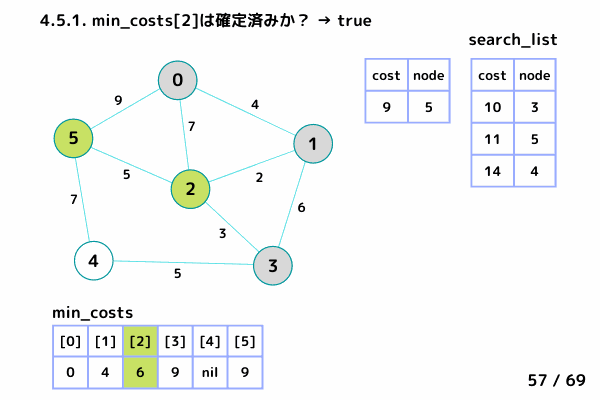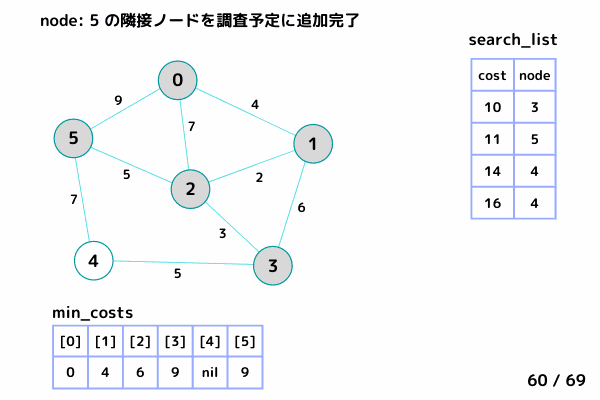
ノード5の処理 (51/69 ～ 61/69)

4.1. 最小コストの要素[cost, node]を取り出す
→ [cost = 9, node= 5]

4.2. min_costs[5]: false → スキップしない

4.3. min_costs[5] = 9 → ノード5 の最小コストを 9 で確定

4.4. min_costsが全て確定したか？: false → 終了しない

4.5. ノード5 の隣接ノードを参照
ノード0, ノード2 は確定済みなのでスキップ
ノード4: [9+7, 4] を search_list に追加

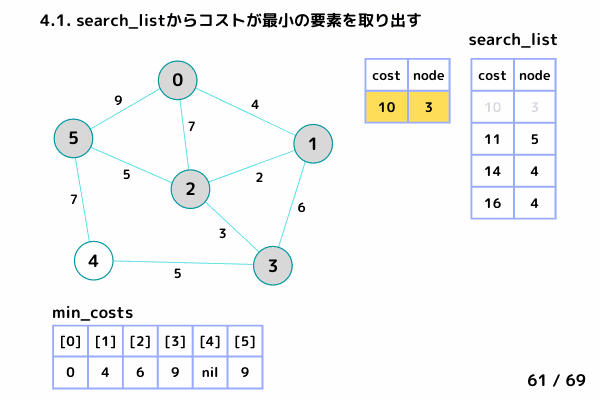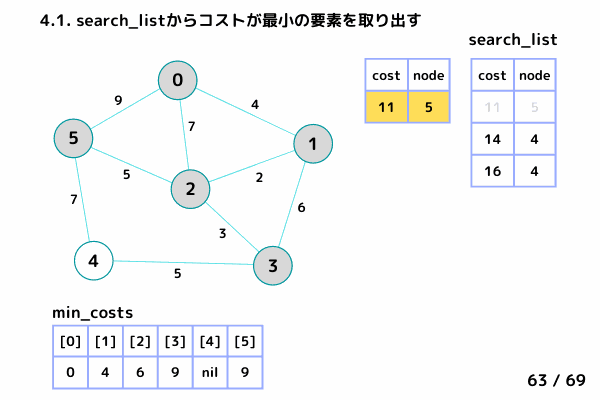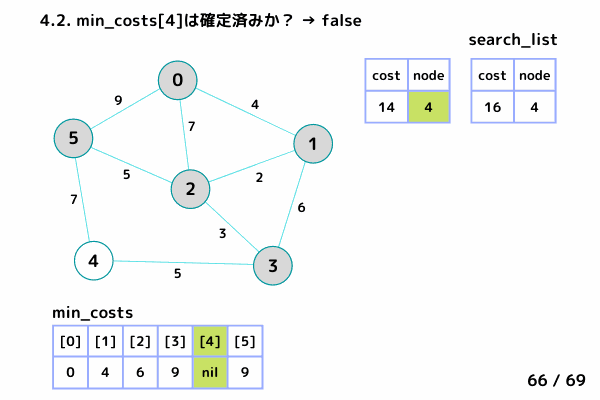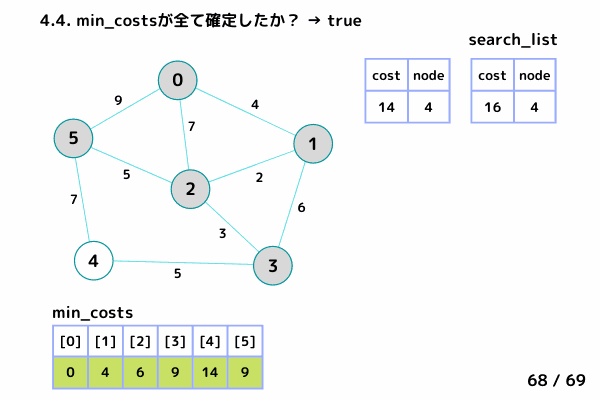
ノード4の処理 (61/69 ～ 68/69)

4.1. 最小コストの要素[cost, node]を取り出す
→ [cost = 10, node= 3], [cost = 11, node= 5] は確定済みなのでスキップ
→ [cost = 14, node= 4]

4.2. min_costs[4]: false → スキップしない

4.3. min_costs[4] = 14 → ノード4 の最小コストを 14 で確定

4.4. min_costsが全て確定したか？: true → ループ終了

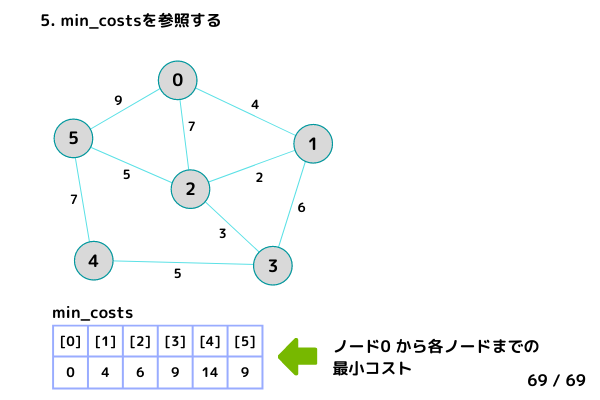
各ノードの最小コストを参照する (69/69)

5. min_costsを参照する(各ノードまでの最小コストが格納されている)

今回のまとめ

• 点と点の繋がりをグラフと言い、グラフの点はノード、辺はエッジ、距離をコスト（重み）と言います。
• 隣接行列や隣接リストでグラフを表現することが出来ます。
• ダイクストラ法は、スタートノード（コスト0）から、一番近い（コストが小さい）ノードを次々に確定させて、探索範囲を増やしていきます。
• 最小コストの要素を探すためのデータ構造に優先度付きキューを使用すると処理が高速になります。

ダイクストラ法は最初難しく感じますが、理解すると「あ、結構単純だったな」となります。
紙にグラフを書いて手書きでコストを計算してみるのもオススメです！

参考文献

Pythonで体験してわかるアルゴリズムとデータ構造（西澤 弘毅、森田 光）