今回はグラフ・DFSメニューから、セクション1「パスの通れない頂点」という問題集を解説します。
グラフとは「交通機関の路線図」や「友達関係」のようなネットワークを表すデータ構造のことで、DFS:DepthFirstSearch(深さ優先探索)とは、一度目指す方向を決めたら、突き当りまで探索を行っていき、最終的に全ての経路を探索する全探索アルゴリズムです。
つまり、グラフをDFS(深さ優先探索)してみよう!という問題集になっています。
セクション1は隣接リスト(adjacency list)の作成や参照から始まって、基本的なDFSを扱う課題で構成されています。
本記事で使用しているメソッド・アルゴリズムについて
解答例で使っているメソッドやアルゴリズムについて、下記の記事で詳しく解説していますので参考にしてみて下さい。
- [Ruby] 標準入力によるデータ取得1
- [Ruby] 標準入力によるデータ取得2
- [Ruby] 標準入力によるデータ取得3
- [Ruby] 標準出力(データを任意に整形して出力する)
- [Ruby]配列の基本操作1
- [Ruby]繰り返し処理
- [Ruby]ハッシュ(連想配列)
- [アルゴリズム]深さ優先探索・幅優先探索
- [データ構造]スタック・キュー・木構造
セクション1【パスの通れない頂点】
STEP1: 隣接頂点の出力 (paizaランク D 相当)
ステップ1は、頂点、枝(経路)、頂点 s が与えられ、頂点 s から移動可能な頂点のうち最も大きい頂点番号を出力する問題です。
入出力例
1行目で頂点数 n と頂点 s が与えられます。
続く 2 * i 行目には 頂点 i に隣接している頂点の数、 2 * i +1 行目には頂点 i に隣接している頂点番号が半角スペース区切りで与えられます。
INPUT1 = <<~"EOS" 3 2 1 2 2 1 3 1 2 EOS OUTPUT1 = <<~"EOS" 3 EOS INPUT2 = <<~"EOS" 5 5 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 4 EOS
INPUT1 はこんな感じ
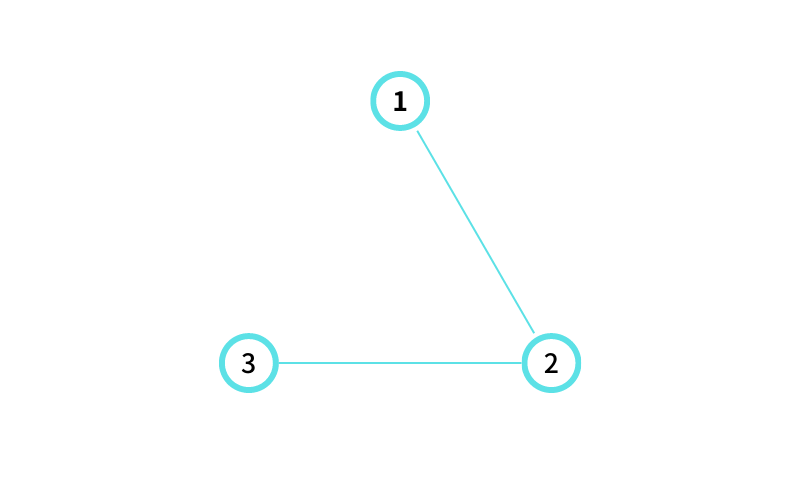
② に隣接する頂点のうち最も番号が大きいのは ③
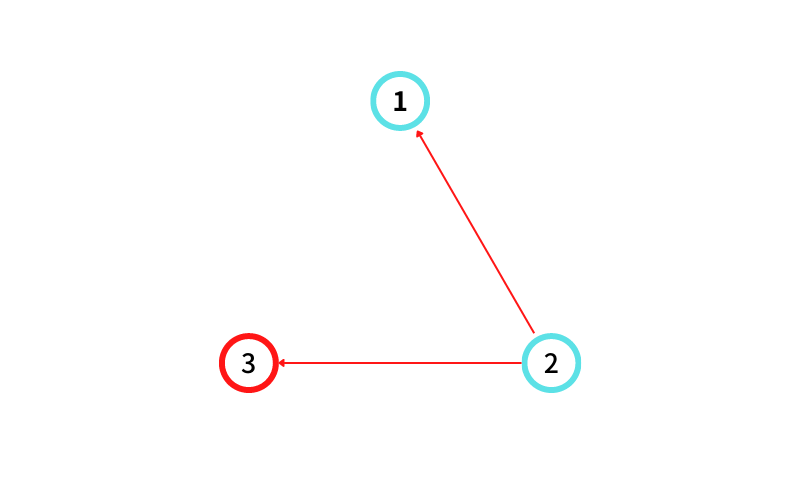
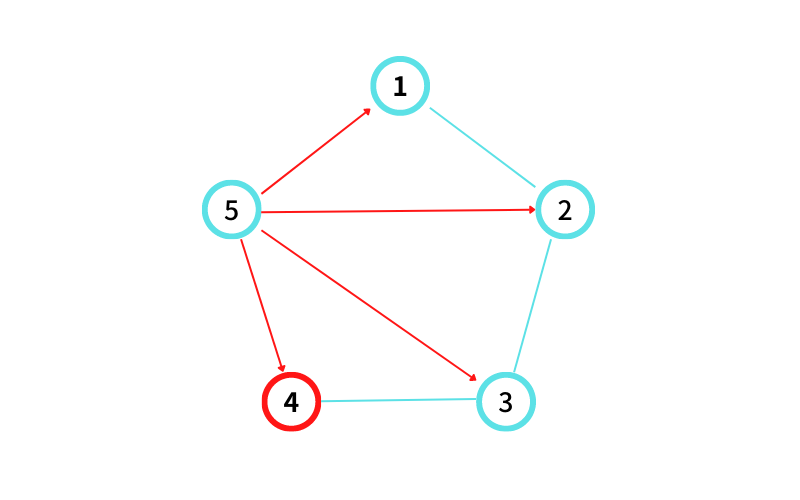
INPUT2 はこんな感じ
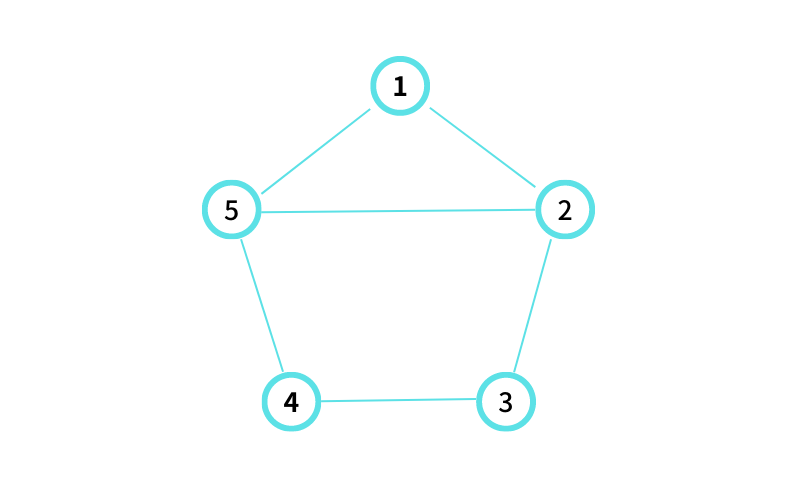
⑤ に隣接する頂点のうち最も番号が大きいのは ④
図を書いてみると分かりやすいですね。これを実装してみます。
Ruby サンプルコード1
とりあえず、 gets メソッドを使って書いてみます。
- 1行目の文字列を半角スペースで区切って整数型に変換して、
n , sに代入する ad_listを空のハッシュで初期化するi = 1からnのループを設定- 経路数を
vに代入する(使わないのでこのまま捨てます。) - 隣接頂点を半角スペースで分割して整数型に変換し、
ad_list[i]に代入する
- 経路数を
ここまで出来たら、 ad_list を確認してみます。
# n: 頂点数, s: 指定の頂点
n, s = gets.split.map(&:to_i)
# 頂点番号 i = 1 から n までの隣接リストを作成
ad_list = {}
1.upto(n) do |i|
# 経路数(使わない)
v = gets
# 経路(頂点番号 i から行ける頂点)
e = gets.split.map(&:to_i)
# ad_list に追加する
ad_list[i] = e
end
p ad_list
# INPUT1 の場合
# > {1=>[2], 2=>[1, 3], 3=>[2]}
# INPUT2 の場合
# > {1=>[2, 5], 2=>[1, 3, 5], 3=>[2, 4, 5], 4=>[3, 5], 5=>[1, 2, 3, 4]}
正しい隣接リストが作られていることが確認出来ました!
…でも、実行するたびに入力データを手入力するのが面倒なので、INPUT1, INPUT2 に定義されているデータをそのまま利用できるようにコードを改造してみようと思います。
Ruby サンプルコード2
入力文字列を引数にとる main メソッドを作成しました。基本的にはサンプルコード1を流用しています。
変更点としては、入力データの2行目を1番に設定してn * 2 行の入力データと番号をセットで参照し、偶数番目の行のデータを半角スペースで分割して整数型に変換し、ad_list[i / 2] に隣接頂点の配列を代入しています。
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 指定の頂点
n, s = input_lines.shift.split.map(&:to_i)
# 頂点番号 i = 1 から n までの隣接リスト作成
ad_list = {}
input_lines.each.with_index(1) do |line, i|
# 経路数 v は使わない
if i.even?
# 隣接リストに経路を格納
ad_list[i / 2] = line.split.map(&:to_i)
end
end
# 確認用コード
ad_list
end
puts main(INPUT1)
# > {1=>[2], 2=>[1, 3], 3=>[2]}
puts main(INPUT2)
# > {1=>[2, 5], 2=>[1, 3, 5], 3=>[2, 4, 5], 4=>[3, 5], 5=>[1, 2, 3, 4]}
これで、入力データを手入力する手間を省きつつ、サンプルコード1と同様に正確な隣接リストを作成することが出来ました。
Ruby サンプルコード3
あとは、 頂点 s に隣接している頂点のうち、最も番号が大きいものを出力します。
ad_list[s].last で隣接する頂点の配列の末尾の要素を取得します。(隣接する頂点の並びは昇順なので末尾が最も大きい番号になっています)
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 指定の頂点
n, s = input_lines.shift.split.map(&:to_i)
# 頂点番号 i = 1 から n までの隣接リスト作成
ad_list = {}
input_lines.each.with_index(1) do |line, i|
# 経路数 v は使わない
if i.even?
# 隣接リストに経路を格納
ad_list[i / 2] = line.split.map(&:to_i)
end
end
# 頂点 s に隣接している頂点の最大番号
ad_list[s].last
end
puts main(INPUT1)
# > 3
puts main(INPUT2)
# > 4
Ruby 解答例
解答を提出するときには、標準入力から入力文字列を受け取れるようにコードを変更します。
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 指定の頂点
n, s = input_lines.shift.split.map(&:to_i)
# 頂点番号 i = 1 から n までの隣接リスト作成
ad_list = {}
input_lines.each.with_index(1) do |line, i|
# 経路数 v は使わない
if i.even?
# 隣接リストに経路を格納
ad_list[i / 2] = line.split.map(&:to_i)
end
end
# 頂点 s に隣接している頂点の最大番号
ad_list[s].last
end
puts main(STDIN.read)
Python解答例
細かい違いはありますが、Pythonでも同様のアプローチで解くことができます。
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 指定の頂点
n, s = map(int, input_lines[0].split())
# 頂点番号 i = 1 から n までの隣接リスト作成
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
# 経路数 v は使わない
if i % 2 == 0:
# 隣接リストに経路を格納
ad_list[i // 2] = list(map(int, line.split()))
# 頂点 s に隣接している頂点の最大番号
return ad_list[s][-1]
print(main(open(0).read()))
STEP2: グラフのウォーク (paizaランク C 相当)
ステップ2は、頂点、枝(経路)、起点 s 、移動回数 k が与えられ、 始点 s から k 回移動する経路を出力する問題です。
- 頂点を再訪問してもOK (walk)
- 経路が複数通りある場合はそのうちのどれか一つを出力すればOK
入出力例
INPUT1 = <<~"EOS" 3 1 2 EOS OUTPUT1 = <<~"EOS" 1 2 1 EOS INPUT2 = <<~"EOS" 5 5 3 EOS OUTPUT2 = <<~"EOS" 5 4 3 4 EOS
INPUT1 はこんな感じ
① からスタートする
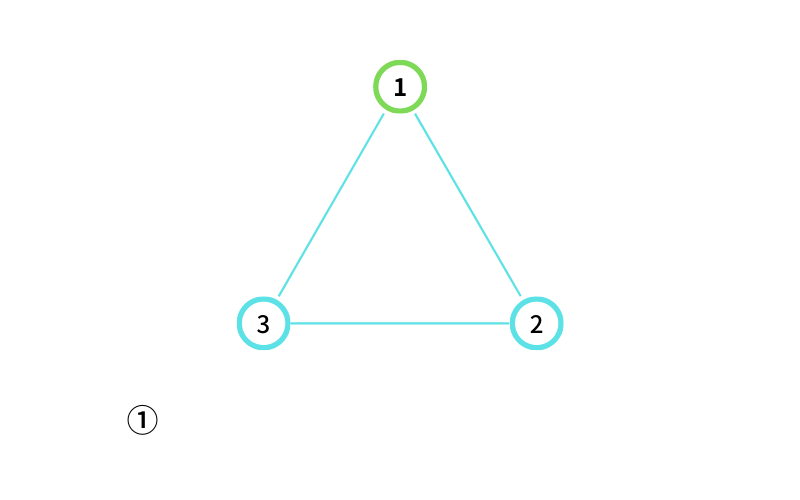
①から ③ に移動する(移動1回目)
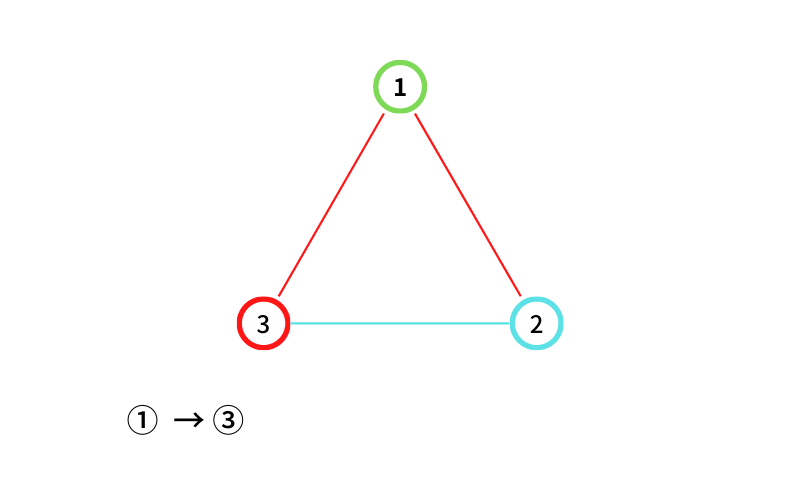
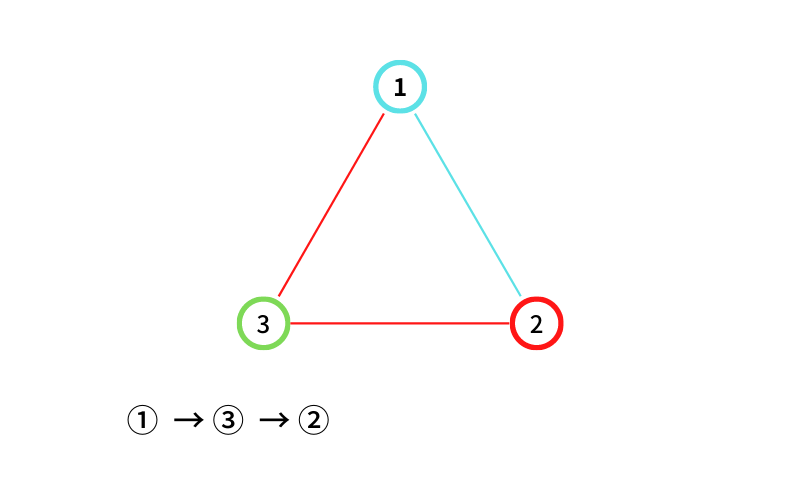
③ から ② に移動する(移動2回目なので終了)
① → ③ → ② という経路が出来た。
※ 他にも経路がありますが、そのうちの一つです。
INPUT2 はこんな感じ
⑤ からスタートする
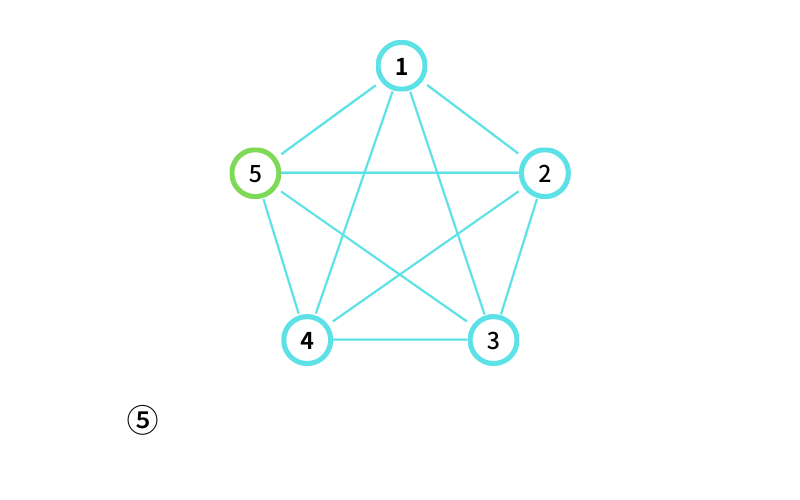
⑤ から ④ に移動する(移動1回目)
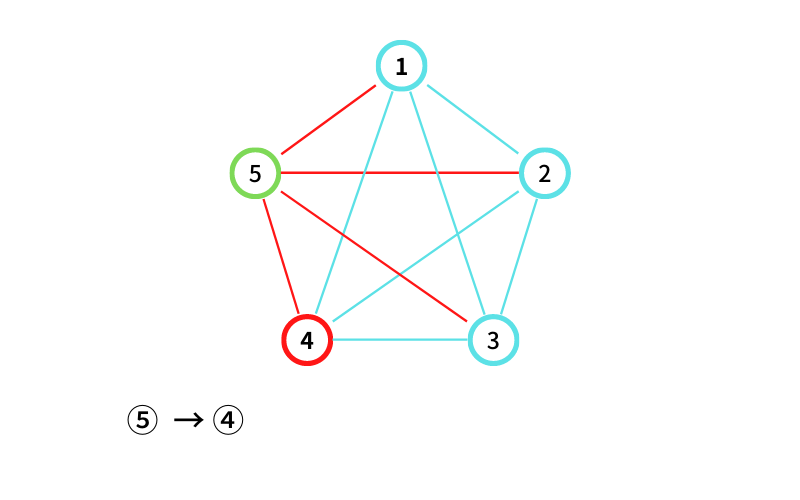
④ から ⑤ に移動する(移動2回目)
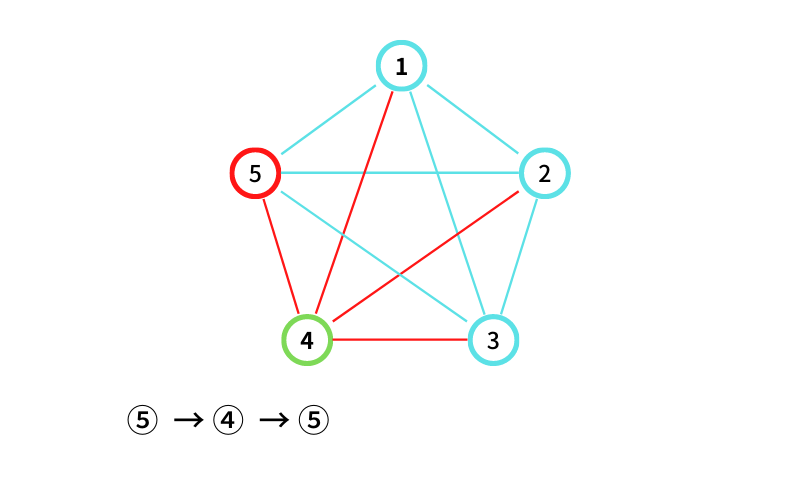
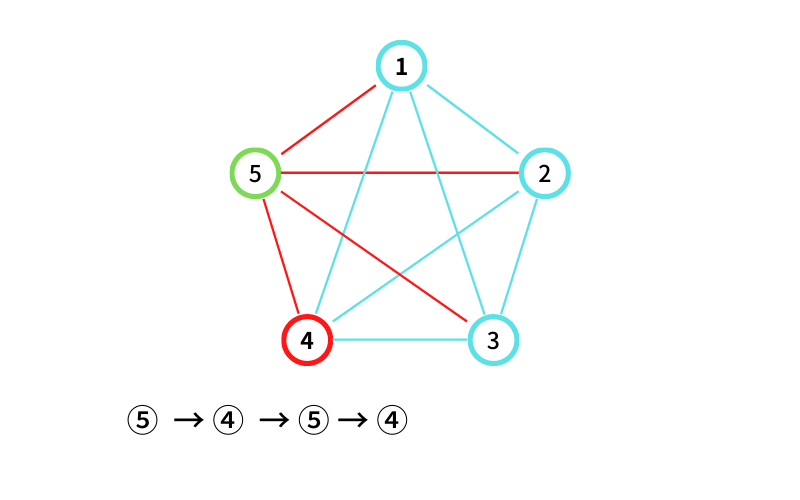
⑤ から ④ に移動する(移動3回目なので終了)
⑤ → ④ → ⑤ → ④ という経路が出来た。
※ 他にも経路がありますが、そのうちの一つです。
Ruby解答例
以下の流れで実装しています。
- 整数 n, s, k を受け取る
- 頂点数 n の、完全無効グラフの隣接リストを作成する
- 起点 s から k 回移動する経路を出力する
(その場その場で最大番号の頂点へ移動するように実装)
def main(input_str)
# n: 頂点数, s: 起点, k: 回数
n, s, k = input_str.split.map(&:to_i)
# 隣接リスト
ad_list = Hash.new { [] }
1.upto(n) do |i|
1.upto(n) do |j|
ad_list[i] <<= j if i != j
end
end
# 起点 s から k 回移動する経路
walk = [s]
k.times do
# 今いる頂点
cv = walk.last
# 移動可能な頂点を選択して walk 末尾へ追加
walk << ad_list[cv].last
end
# 経路を出力
walk.join(" ")
end
puts main(STDIN.read)
Python解答例
今回もRubyと同様のアプローチで解くことが出来ます。
隣接リスト生成にリスト内包表記を使ってみました。リスト内包表記便利!
def main(input_str):
# n: 頂点数, s: 起点, k: 回数
n, s, k = map(int, input_str.split())
# 隣接リスト
ad_list = {}
for i in range(1, n + 1):
ad_list[i] = [j for j in range(1, n + 1) if j != i]
# 起点 s から k 回移動する経路
walk = [s]
for _ in range(k):
# 今いる頂点
cv = walk[-1]
# 移動可能な頂点を選択して walk 末尾へ追加
walk.append(ad_list[cv][-1])
# 経路を出力
return " ".join(map(str, walk))
print(main(open(0).read()))
STEP3: グラフのパス (paizaランク C 相当)
ステップ3は、頂点数 n の完全無向グラフ、起点 s 、移動回数 k が与えられ、 k 回移動した場合の経路を出力する問題です。
- 完全無向グラフとは、任意の2頂点の経路が必ず存在するグラフ
- 訪問済みの頂点は再訪問できない (path) ← 重要ポイント!
- 経路が複数通りある場合はそのうちのどれか一つを出力すればOK
入出力例
INPUT1 = <<~"EOS" 3 1 2 EOS OUTPUT1 = <<~"EOS" 1 2 3 EOS INPUT2 = <<~"EOS" 5 5 3 EOS OUTPUT2 = <<~"EOS" 5 4 3 2 EOS
INPUT1 はこんな感じ
① からスタートする
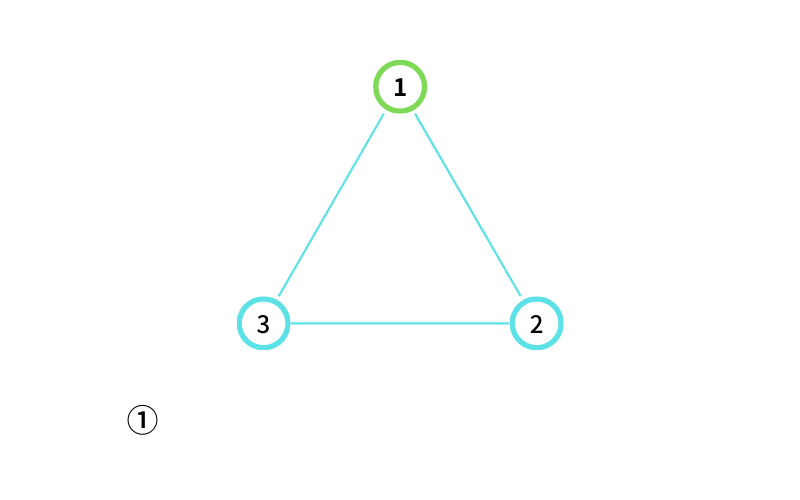
① から ③ に移動する(移動1回目)
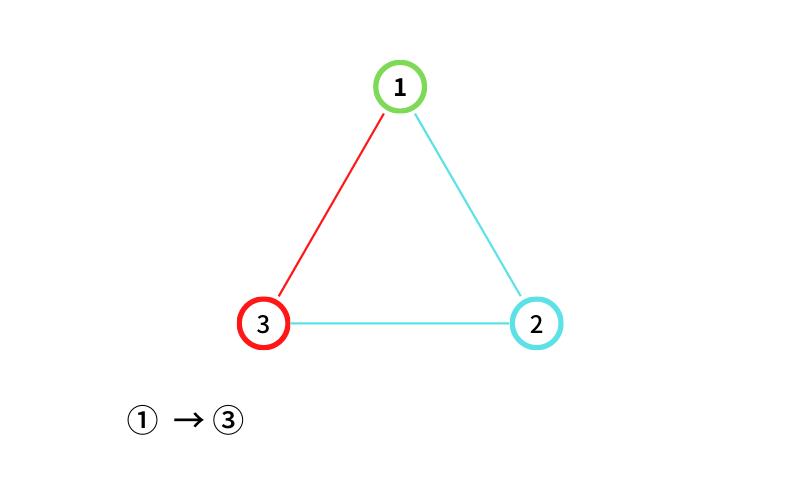
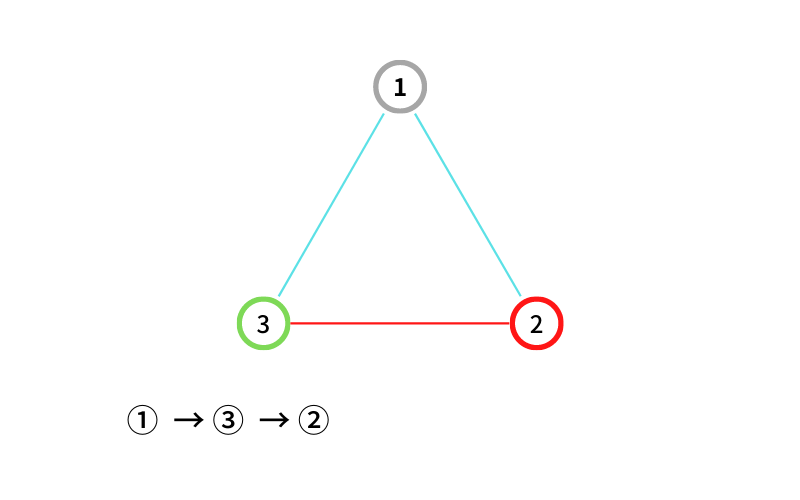
③ から ② に移動する(移動2回目なので終了)
① → ③ → ② という経路が出来た。
※ 他にも経路がありますが、そのうちの一つです。
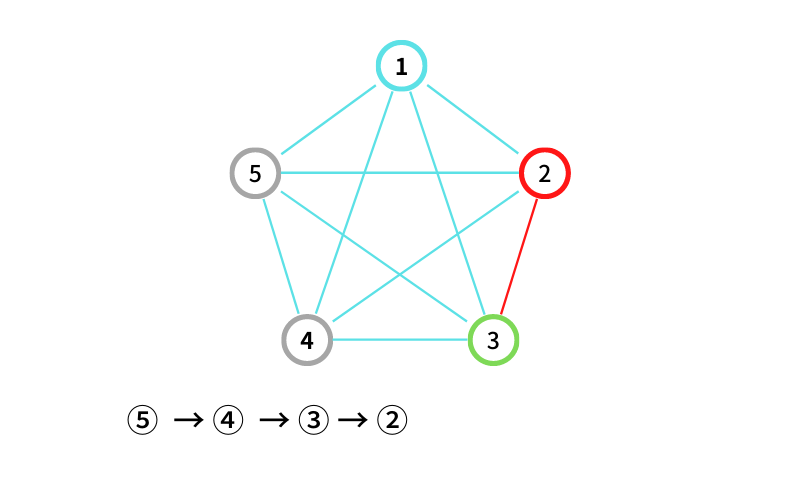
INPUT2 はこんな感じ
⑤ からスタートする
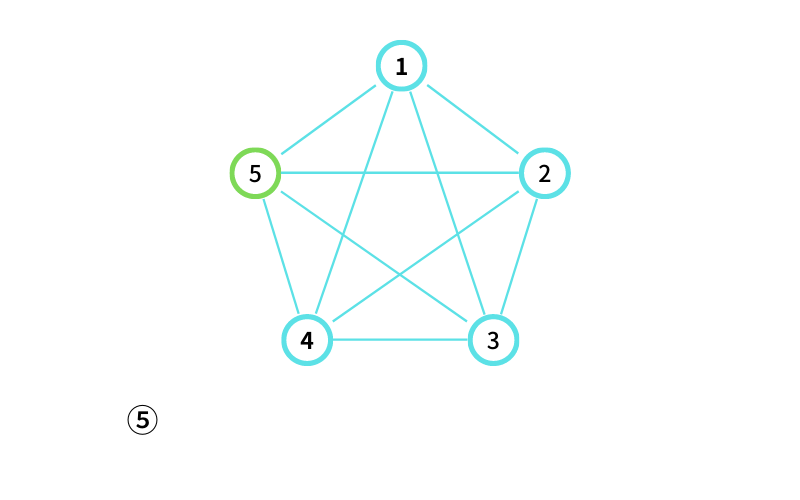
⑤ から ④ に移動する(移動1回目)
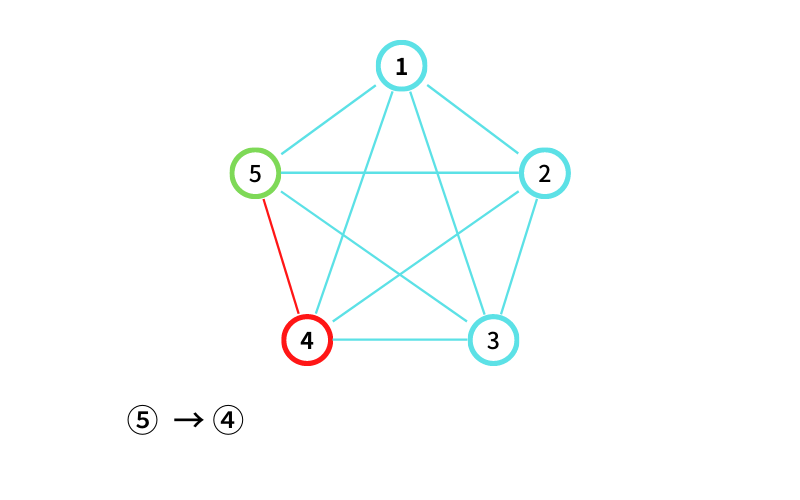
④ から ③ に移動する(移動2回目)
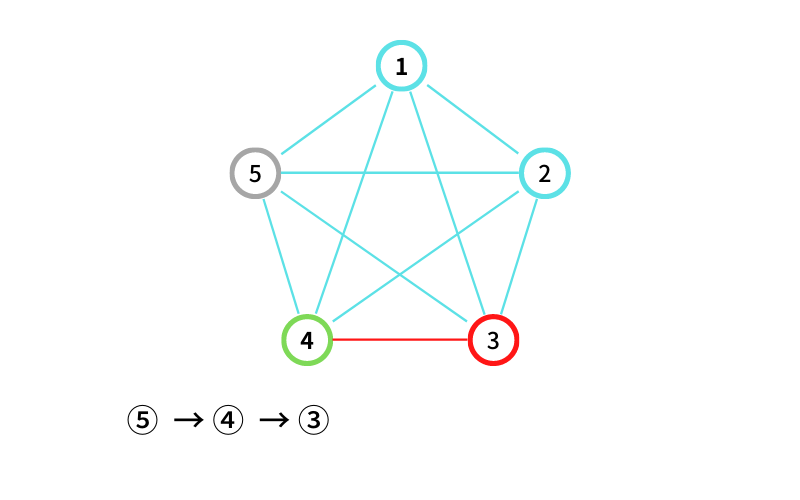
③ から ② に移動する(移動2回目なので終了)
⑤ → ④ → ③ → ② という経路が出来た。
※ 他にも経路がありますが、そのうちの一つです。
Ruby解答例
前回までのコードを流用して解くことが出来ます。
今回のポイントは、頂点を再訪問出来ないという制約です。
def main(input_str)
# n: 頂点数, s: 起点, k: 回数
n, s, k = input_str.split.map(&:to_i)
# 隣接リスト
ad_list = Hash.new { [] }
1.upto(n) do |i|
1.upto(n) do |j|
ad_list[i] <<= j if i != j
end
end
# s から k 回移動する経路
path = [s]
k.times do
# 今いる頂点
cv = path.last
# 移動可能な未訪問の頂点を末尾に追加する
ad_list[cv].reverse.each do |nv|
# 訪問済の頂点はスキップ
next if path.include?(nv)
# path に追加してループを抜ける
path << nv
break
end
end
# 経路を出力
path.join(" ")
end
puts main(STDIN.read)
Python解答例
def main(input_str):
# n: 頂点数, s: 起点, k: 回数
n, s, k = map(int, input_str.split())
# 隣接リスト
ad_list = {}
for i in range(1, n + 1):
e = [j for j in range(1, n + 1) if j != i]
ad_list[i] = e
# s から k 回移動する経路
path = [s]
for _ in range(k):
# 今いる頂点
cv = path[-1]
# 移動可能な頂点を選択して walk 末尾へ追加
for nv in ad_list[cv][::-1]:
# 訪問済の頂点はスキップ
if nv in path:
continue
# path に追加してループを抜ける
path.append(nv)
break
# 経路を出力
return " ".join(map(str, path))
print(main(open(0).read()))
STEP4: グラフの s,t パス (paizaランク B 相当)
ステップ4は、頂点、枝(経路)、起点 s 、終点 t が与えられ、 始点 s から 終点 t まで移動できる経路のうち、訪問頂点数が最も少ないものを出力する問題です。
- 起点
sから終点tに行ける経路は必ず存在する - 同じ頂点は再訪問できない (path)
- 経路が複数通りある場合は、そのうちのどれか一つを出力すればOK
入出力例
INPUT1 = <<~"EOS" 5 1 4 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT1 = <<~"EOS" 1 5 4 EOS INPUT2 = <<~"EOS" 5 5 3 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 5 3 EOS
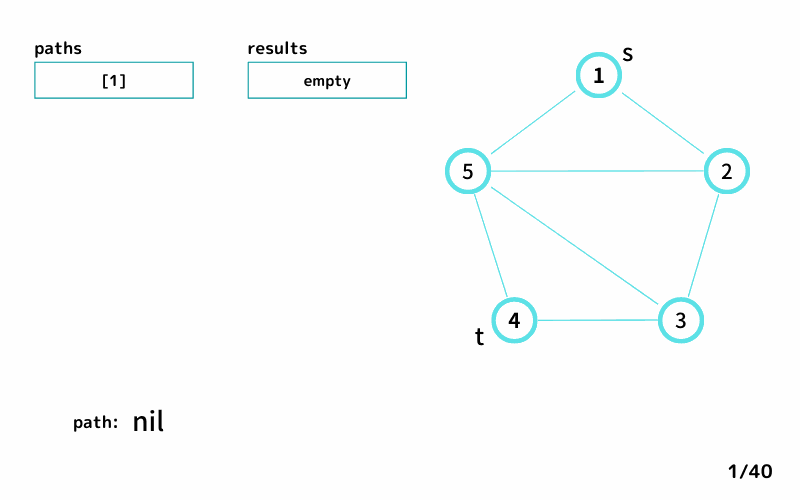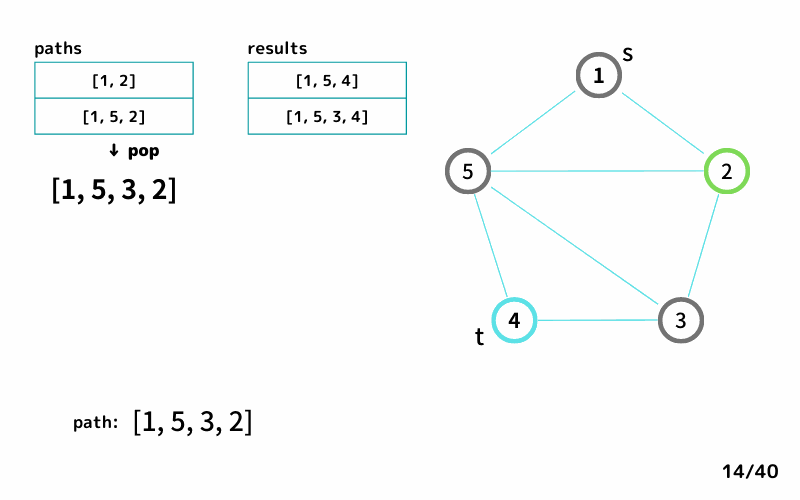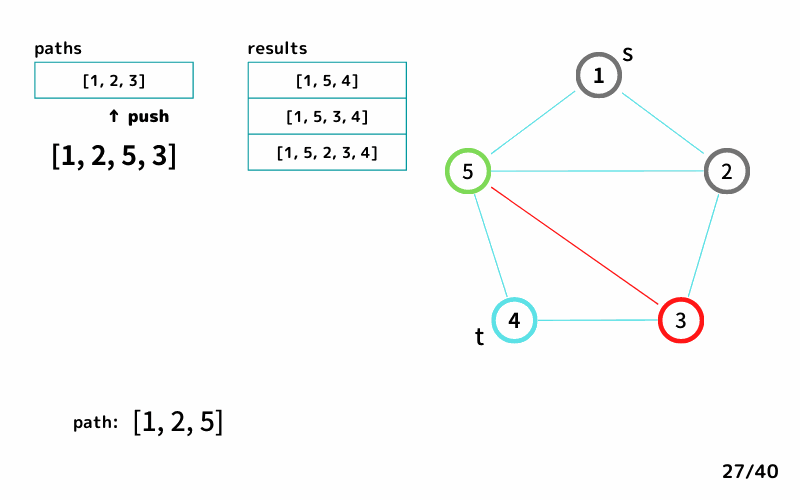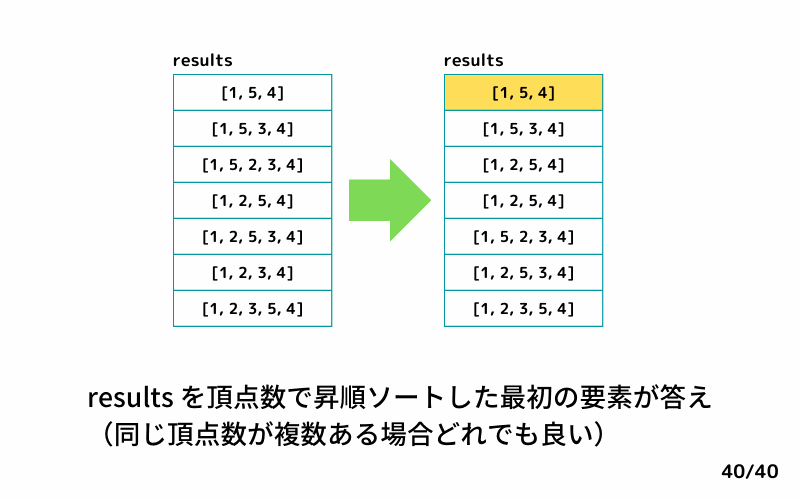
どんな感じで 始点 s から終点 t への経路を列挙するのかを、INPUT1を例にgifアニメにしてみました。
Ruby解答例
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, t: 終点
n, s, t = input_lines.shift.split.map(&:to_i)
# 隣接リスト
ad_list = {}
input_lines.each.with_index(1) do |line, i|
# 経路数 v は使わない
if i.even?
ad_list[i / 2] = line.split.map(&:to_i)
end
end
# s から t への経路
results = []
paths = [[s]]
while paths.length > 0
path = paths.pop
# t に着いたら経路を記録
if path.last == t
results << path
next
end
# 未訪問の隣接頂点に移動する
cv = path.last
ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if path.include?(nv)
# 新しい経路を追加
paths << path + [nv]
end
end
# s から t に行ける経路を頂点数で昇順ソート
results.sort! { |a, b| a.length <=> b.length }
# 最も頂点数が少ない経路を出力
results.first.join(" ")
end
puts main(STDIN.read)
Python解答例
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, t: 終点
n, s, t = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
# 経路数 v は使わない
if i % 2 == 0:
# 隣接リストに経路を格納
ad_list[i // 2] = list(map(int, line.split()))
# s から t への経路
results = []
paths = [[s]]
while len(paths) > 0:
path = paths.pop()
# t に着いたら経路を記録
if path[-1] == t:
results.append(path)
continue
# 未訪問の隣接頂点に移動する
cv = path[-1]
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in path:
continue
# 新しい経路を追加
paths.append(path + [nv])
# s から t に行ける経路を頂点数で昇順ソート
results.sort(key=lambda x: len(x))
# 最も頂点数が少ない経路を出力
return " ".join(map(str, results[0]))
print(main(open(0).read()))
STEP5: パスの経由地 (paizaランク B 相当)
ステップ5は、頂点、枝(経路)、起点 s 、終点 t 、中継点 q が与えられ、 始点 s から 中継点 q を経由して 終点 t まで移動できる経路のうち、訪問頂点数が最も少ないもの、または経路が存在しない場合は -1 を出力する問題です。(※ 本家では中継点 p となっていますが、 p という変数を使いたくないので p → q に変更しました)
・訪問済みの頂点は再訪問できない (path)
・経路が複数通りある場合はそのうちのどれか一つを出力すればOK
入出力例
INPUT1 = <<~"EOS" 5 1 4 3 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT1 = <<~"EOS" 1 2 3 4 EOS INPUT2 = <<~"EOS" 5 5 3 1 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 5 1 2 3 EOS INPUT3 = <<~"EOS" 8 8 4 1 1 2 7 1 3 4 5 6 7 8 6 2 4 5 6 7 8 6 2 3 5 6 7 8 6 2 3 4 6 7 8 6 2 3 4 5 7 8 6 2 3 4 5 6 8 6 2 3 4 5 6 7 EOS OUTPUT3 = <<~"EOS" -1 EOS
Ruby解答例
今回も前回のコードを流用します。
問題文を読むと難しく感じますが、結局のところ、始点 s から 終点 t まで行ける経路のうち、中継点 q を含む経路を探せば良いだけです。
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, t: 終点, q: 中継点
n, s, t, q = input_lines.shift.split.map(&:to_i)
# 隣接リスト
ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
ad_list[i / 2] = line.split.map(&:to_i)
end
# q を経由して s から t へ行ける経路
results = []
paths = [[s]]
while paths.length > 0
path = paths.pop
# q を経由して t に着いたら経路を記録
if path.last == t && path.include?(q)
results << path
next
end
# 未訪問の隣接頂点に移動する
cv = path.last
ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if path.include?(nv)
# 新しい経路を追加
paths << path + [nv]
end
end
# 頂点が最も少ない経路、または -1 を出力
if results.length > 0
# 経路の頂点数で昇順ソート
results.sort! { |a, b| a.length <=> b.length }
# 最も頂点数が少ない経路を出力
results.first.join(" ")
else
# 該当経路なしなら -1 を出力
-1
end
end
puts main(STDIN.read)
Python解答例
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, t: 終点, q: 中継点
n, s, t, q = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
# 経路数 v は使わない
if i % 2 == 0:
# 隣接リストに経路を格納
ad_list[i // 2] = list(map(int, line.split()))
# s から q を経由して t へ行ける経路
results = []
paths = [[s]]
while len(paths) > 0:
path = paths.pop()
# t に着いたら経路を記録
if path[-1] == t and q in path:
results.append(path)
continue
# 未訪問の隣接頂点に移動する
cv = path[-1]
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in path:
continue
# 新しい経路を追加
paths.append(path + [nv])
# 頂点が最も少ない経路、または -1 を出力
if len(results) > 0:
# s から t に行ける経路を頂点数で昇順ソート
results.sort(key=lambda x: len(x))
# 最も頂点数が少ない経路を出力
return " ".join(map(str, results[0]))
else:
return -1
print(main(open(0).read()))
FINAL: パスの通れない頂点 (paizaランク B 相当)
ステップ6は、頂点、枝(経路)、訪問出来ない頂点、起点 s 、終点 t が与えられ、 始点 s から 終点 t まで移動できる経路のうち、訪問頂点数が最も少ないもの、または経路が存在しない場合は -1 を出力する問題です
・訪問済みの頂点は再訪問できない (path)
・経路が複数通りある場合はそのうちのどれか一つを出力すればOK
入出力例
INPUT1 = <<~"EOS" 5 1 4 3 2 3 5 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT1 = <<~"EOS" -1 EOS INPUT2 = <<~"EOS" 5 5 3 3 1 2 4 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 5 3 EOS INPUT3 = <<~"EOS" 8 1 5 2 3 7 3 2 3 7 4 1 3 7 8 7 1 2 4 5 6 7 8 4 3 6 7 8 3 3 6 7 4 3 4 5 7 7 1 2 3 4 5 6 8 4 2 3 4 7 EOS OUTPUT3 = <<~"EOS" 1 2 8 4 6 5 EOS
Ruby解答例
今回も前回のコードを流用します。
訪問しない頂点を配列で記録しておき、探索候補の頂点が訪問しない頂点なら、探索候補から除外すれば良いだけです。
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, t: 終点
n, s, t = input_lines.shift.split.map(&:to_i)
# 通らない頂点
unused_vertices = input_lines.shift(2).last.split.map(&:to_i)
# 隣接リスト
ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
ad_list[i / 2] = line.split.map(&:to_i)
end
# 始点 s から終点 t までの経路
results = []
paths = [[s]]
while paths.length > 0
path = paths.pop
if path.last == t
results << path
next
end
# 未訪問の隣接頂点に移動する
cv = path.last
ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if path.include?(nv)
# 通れない頂点はスキップ
next if unused_vertices.include?(nv)
# 新しい経路を追加
paths << path + [nv]
end
end
# 頂点が最も少ない経路または -1 を出力
if results.length > 0
# 経路の頂点数で昇順ソート
results.sort! { |a, b| a.length <=> b.length }
# 最も頂点数が少ない経路を出力
results.first.join(" ")
else
# 経路なしなら -1 を出力
-1
end
end
puts main(STDIN.read)
Python解答例
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, t: 終点
n, s, t = map(int, input_lines[0].split())
# 通らない頂点
unused_vertices = list(map(int, input_lines[2].split()))
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[3:], 1):
# 経路数 v は使わない
if i % 2 == 0:
# 隣接リストに経路を格納
ad_list[i // 2] = list(map(int, line.split()))
# s から t へ行ける経路を調べる
results = []
paths = [[s]]
while len(paths) > 0:
path = paths.pop()
# t に着いたら経路を記録
if path[-1] == t:
results.append(path)
continue
# 未訪問の隣接頂点に移動する
cv = path[-1]
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in path or nv in unused_vertices:
continue
# 新しい経路を追加
paths.append(path + [nv])
# 頂点が最も少ない経路、または -1 を出力
if len(results) > 0:
# s から t に行ける経路を頂点数で昇順ソート
results.sort(key=lambda x: len(x))
# 最も頂点数が少ない経路を出力
return " ".join(map(str, results[0]))
else:
return -1
print(main(open(0).read()))
今回のまとめ
- DFS(深さ優先探索)は、スタック構造で実装できる!
- ウォーク (walk) は頂点の反復を許す経路
- パス (path) は頂点の反復を許さない経路

今回は、グラフ構造に対する深さ優先探索を紹介しました。
paizaの解説では再帰呼び出しを使っていますが、ちゃんと理解していないと色々大変なので、私は今のところ今回紹介したようなコードで再帰を回避しています。(汗)
この問題集では全ての問題で全探索しても時間オーバーになりませんが、別の問題では探索打ち切りが必要な場合も考えられます。
解説コードでも計算量を削減出来る箇所があるなぁと思いつつ、そのまま載せていますので、もし余裕があれば計算量削減も考えてみましょう!




