今回はpaiza リアルイベント問題セット ハノイの塔 (paizaランク A 相当)を解説します。
知育玩具としても販売されている「ハノイの塔」というパズルを最小の手数で解く時に、指定された手数の状態を表示する問題です。
ハノイの塔 (paizaランク A 相当) を解いてみる
※ paiza リアルイベント問題セット より
問題
ハノイの塔というパズルがあります。
3つの杭があり、左から順にA,B,Cの杭とします。
杭Aに円盤が下から大きい順に n 個重なって置かれています。
この円盤は必ず1つ上の円盤は下の円盤より小さくなくてはいけないルールがあります。
このルールを守りながらAの杭からCの杭へ円盤を動かす操作をするパズルです。
例えば3つの円盤が入力として与えられる場合、その時の最短手順は以下の通りになります。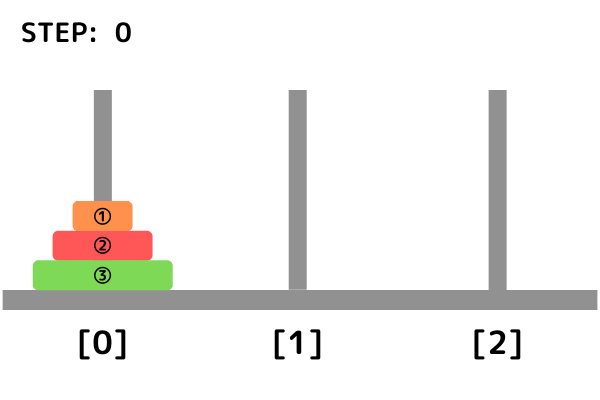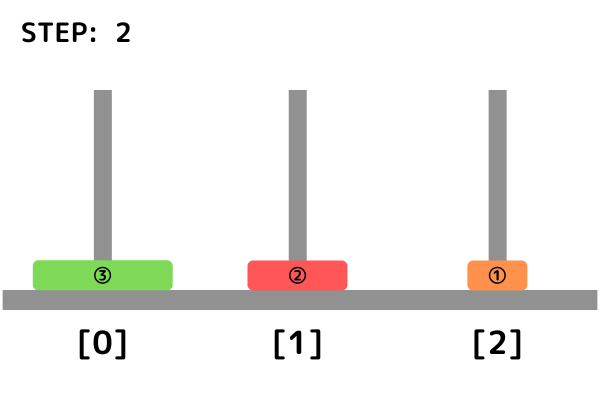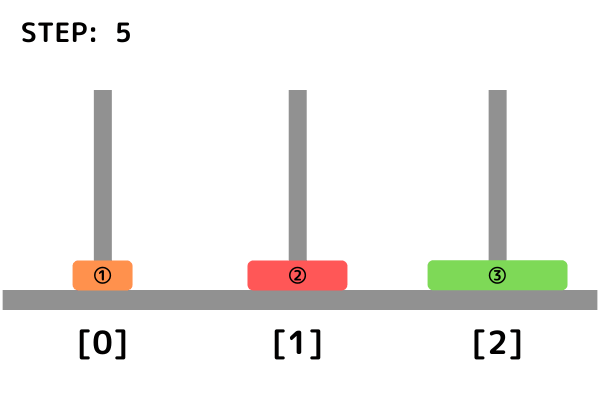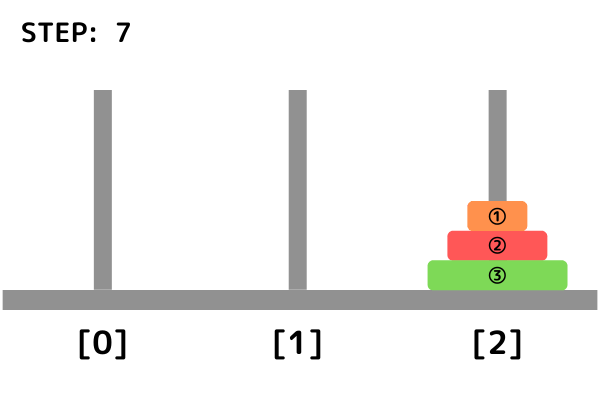
この時、円盤の数によらず最短手順は常に一意に決まります。
円盤の数 n が与えられます。1つも動かしていない状態を t = 0 とし、円盤を動かした回数を t とします。
円盤の数 n と、円盤を動かした回数 t が与えられるので n 個の円盤を最短手順で動かしていった時に円盤を動かした回数 t の状態を出力してください。
入力される値
入力は以下のフォーマットで与えられます。
n t
入力値最終行の末尾に改行が1つ入ります。
期待する出力
n 個の円盤を最短手順で動かして行った時、 t 回動かした時点の各杭に積み上がっている円盤を出力してください。
1行目を杭A、2行目を杭B、3行目を杭Cとし、各行の一番左を杭の一番下として円盤の大きさを 1 から n の数字でスペース区切りで出力して下さい。
1つも円盤がない杭の行には「-」と出力して下さい。
条件
すべてのテストケースにおいて、以下の条件をみたします。
- 1 ≦ n ≦ 16
- 1 ≦ t ≦ 2^n - 1
- 入力例1
- 3 4
- 出力例1
- -
2 1
3
- 入力例2
- 4 6
- 出力例2
- 4 1
3 2
-
攻略ポイント
ポイント
- ハノイの塔の解き方を整理する
- n = 1
- 1番の円盤を杭Aから杭Cに移動する
- n ≧ 2
- 1~n-1番までの円盤を杭Bに移動する
- n番の円盤を杭Cに移動する
- 1~n-1番までの円盤を杭Cに移動する
- n = 1
メソッドの定義と呼び出し
問題を解く流れ
入出力例をコピペしてヒアドキュメントで変数に代入し、データを確認します。正しく受け取れていれば確認用コードは削除します。
INPUT1 = <<~"EOS" 3 4 EOS OUTPUT1 = <<~"EOS" - 2 1 3 EOS INPUT2 = <<~"EOS" 4 6 EOS OUTPUT2 = <<~"EOS" 4 1 3 2 - EOS # 確認用コード p INPUT1 # > "3 4\n" p OUTPUT1 # > "-\n2 1\n3\n" p INPUT2 # > "4 6\n" p OUTPUT2 # > "4 1\n3 2\n-\n"
続いて問題を解くメソッド( solve メソッドとします)を変数の下に定義します。
まず、入力データを受け取る処理を書きます。
def solve(input_lines) n, t = input_lines.split.map(&:to_i) # 確認用コード [n, t] end # 確認用コード p solve(INPUT1) # > [3, 4] p solve(INPUT2) # > [4, 6]
データが正しく受け取れていれば、ハノイの塔を解くhanoiメソッドを追加します。
hanoi(k, start, work, goal)
k: 円盤の数, start: 移動元の杭, work: 作業用の杭, goal: 移動先の杭
- 円盤の数が1になるまで
hanoi(k-1, start, goal, work)を呼び出す - startの円盤をgoalに移動する
- 円盤の数が1になるまで
hanoi(k-1, work, start, goal)を呼び出す
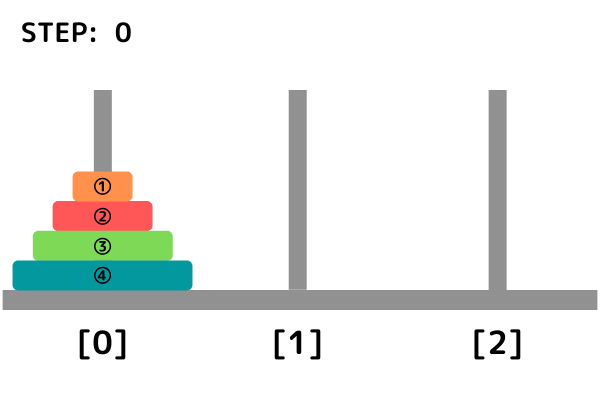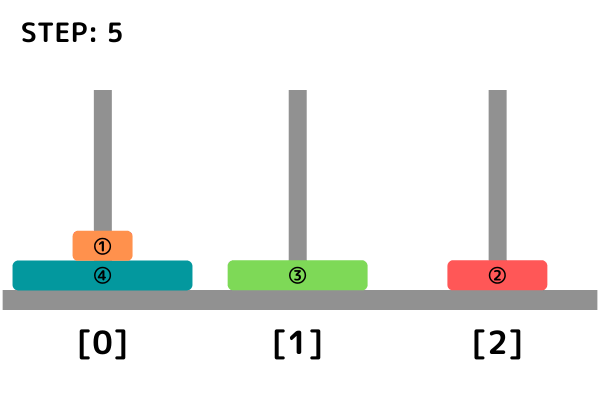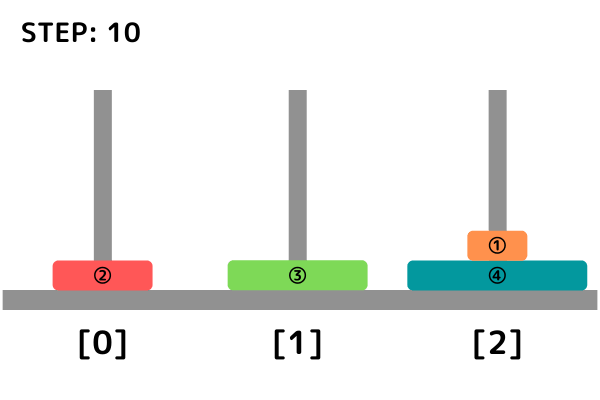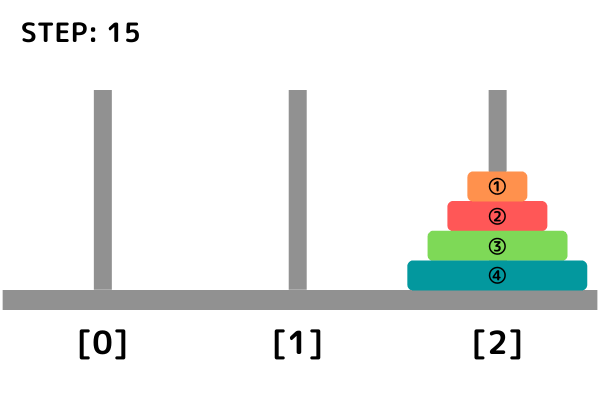
再帰呼び出しのイメージ(INPUT1)
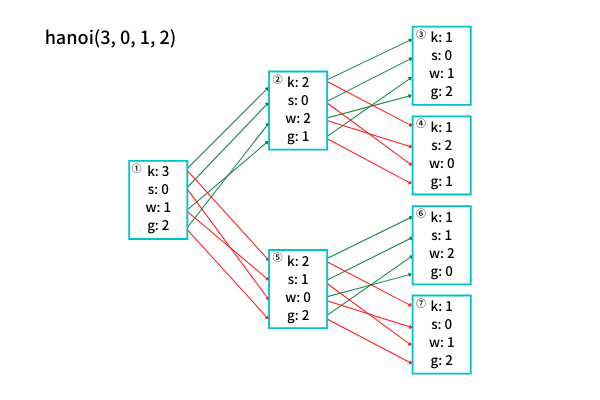
- ③ → ② → ④ → ① → ⑥ → ⑤ → ⑦ の順番でstartからgoalへ円盤を動かす
- ③ → ② → ④ : 1~n-1番目までの円盤を杭Aから杭Bへ動かす
- ① : n番目の円盤を杭Aから杭Cへ動かす
- ⑥ → ⑤ → ⑦ : 1~n-1番目までの円盤を杭Bから杭Cへ動かす
※ n段の塔の最少手数は t = 2^k-1 となります。(n=3 -> t=7, n=4 -> t=15)
円盤移動のイメージ
INPUT1

INPUT2
def hanoi(k, start, work, goal)
hanoi(k - 1, start, goal, work) if k > 1
# 確認用コード
puts "#{start} の円盤を #{goal} に移動する"
hanoi(k - 1, work, start, goal) if k > 1
end
def solve(input_lines)
n, t = input_lines.split.map(&:to_i)
# 確認用コード
puts "#{n} 段"
hanoi(n, 0, 1, 2)
puts "---------"
end
# 確認用コード
solve(INPUT1)
# > 3 段
# > 0 の円盤を 2 に移動する
# > 0 の円盤を 1 に移動する
# > 2 の円盤を 1 に移動する
# > 0 の円盤を 2 に移動する
# > 1 の円盤を 0 に移動する
# > 1 の円盤を 2 に移動する
# > 0 の円盤を 2 に移動する
# > ---------
solve(INPUT2)
# > 4 段
# > 0 の円盤を 1 に移動する
# > 0 の円盤を 2 に移動する
# > 1 の円盤を 2 に移動する
# > 0 の円盤を 1 に移動する
# > 2 の円盤を 0 に移動する
# > 2 の円盤を 1 に移動する
# > 0 の円盤を 1 に移動する
# > 0 の円盤を 2 に移動する
# > 1 の円盤を 2 に移動する
# > 1 の円盤を 0 に移動する
# > 2 の円盤を 0 に移動する
# > 1 の円盤を 2 に移動する
# > 0 の円盤を 1 に移動する
# > 0 の円盤を 2 に移動する
# > 1 の円盤を 2 に移動する
# > ---------
ハノイの塔を解く手順は分かったので、指定された手数での状態を出力する処理を追加します。
- 塔(杭)の状態管理用のグローバル変数: $towers を用意する
- 円盤の移動記録用のグローバル変数: $result を用意する
- hanoiメソッドの中から $towers を更新し、$resultに記録する
def hanoi(k, start, work, goal)
hanoi(k - 1, start, goal, work) if k > 1
$towers[goal] << $towers[start].pop
$result << $towers.map { |t| t.empty? ? "-" : t.join(" ") }.join("\n")
hanoi(k - 1, work, start, goal) if k > 1
end
def solve(input_lines)
n, t = input_lines.split.map(&:to_i)
# 現在の杭(塔)の状態
$towers = [(1..n).to_a.reverse, [], []]
# 円盤移動の記録
$result = []
hanoi(n, 0, 1, 2)
# 確認用コード
$result
end
# 確認用コード
pp solve(INPUT1)
# > ["3 2\n" + "-\n" + "1",
# > "3\n" + "2\n" + "1",
# > "3\n" + "2 1\n" + "-",
# > "-\n" + "2 1\n" + "3",
# > "1\n" + "2\n" + "3",
# > "1\n" + "-\n" + "3 2",
# > "-\n" + "-\n" + "3 2 1"]
pp solve(INPUT2)
# > ["4 3 2\n" + "1\n" + "-",
# > "4 3\n" + "1\n" + "2",
# > "4 3\n" + "-\n" + "2 1",
# > "4\n" + "3\n" + "2 1",
# > "4 1\n" + "3\n" + "2",
# > "4 1\n" + "3 2\n" + "-",
# > "4\n" + "3 2 1\n" + "-",
# > "-\n" + "3 2 1\n" + "4",
# > "-\n" + "3 2\n" + "4 1",
# > "2\n" + "3\n" + "4 1",
# > "2 1\n" + "3\n" + "4",
# > "2 1\n" + "-\n" + "4 3",
# > "2\n" + "1\n" + "4 3",
# > "-\n" + "1\n" + "4 3 2",
# > "-\n" + "-\n" + "4 3 2 1"]
円盤の移動手順が$resultに正しく記録されていれば、t手目($result[t-1])の状態を出力すれば完成です。
def hanoi(k, start, work, goal)
hanoi(k - 1, start, goal, work) if k > 1
$towers[goal] << $towers[start].pop
$result << $towers.map { |t| t.empty? ? "-" : t.join(" ") }.join("\n")
hanoi(k - 1, work, start, goal) if k > 1
end
def solve(input_lines)
n, t = input_lines.split.map(&:to_i)
# 現在の杭(塔)の状態
$towers = [(1..n).to_a.reverse, [], []]
# 円盤移動の記録
$result = []
hanoi(n, 0, 1, 2)
# t 手目の状態を返す
$result[t - 1] << "\n"
end
# 確認用コード
p solve(INPUT1)
# > "-\n2 1\n3\n"
p solve(INPUT1) == OUTPUT1
# > true
p solve(INPUT2)
# > "4 1\n3 2\n-\n"
p solve(INPUT2) == OUTPUT2
# > true
確認用コードを標準入力からのデータ受け取りに変更、標準出力をpメソッドからputsメソッドに変更して、動作確認をしたら提出します。(STDIN.readの入力終了は Ctrl+D 又は Ctrl+Z)
解答コード
def hanoi(k, start, work, goal)
hanoi(k - 1, start, goal, work) if k > 1
$towers[goal] << $towers[start].pop
$result << $towers.map { |t| t.empty? ? "-" : t.join(" ") }.join("\n")
hanoi(k - 1, work, start, goal) if k > 1
end
def solve(input_lines)
n, t = input_lines.split.map(&:to_i)
# 現在の杭(塔)の状態
$towers = [(1..n).to_a.reverse, [], []]
# 円盤移動の記録
$result = []
hanoi(n, 0, 1, 2)
# t 手目の状態を返す
$result[t - 1] << "\n"
end
puts solve(STDIN.read)
他の解答例
再帰でハノイの塔を解こうとすると、2^n-1回、hanoiメソッドを呼び出します。
問題では16段までだったので、最大2^16 - 1 = 65535回でしたが、100段の問題を解こうとすると、
2^100 - 1 = 1,267,650,600,228,229,401,496,703,205,375
つまり、126穣(じょう)7650𥝱(じょ)6002垓(がい)2822京9401兆4967億320万5375回 hanoiメソッドを呼び出すことになり、気が遠くなる時間がかかります。
(実際は再帰呼び出しには限界があるので途中でエラーが出ます。)
というわけで100段の問題を解くための工夫を検討してみます。
円盤個数n = 1 〜 4 までを最短手順で動かしたときに各円盤がどの様に動くかをまとめた表を作成しました。
表を見ると円盤の状態に規則性があることがわかります。
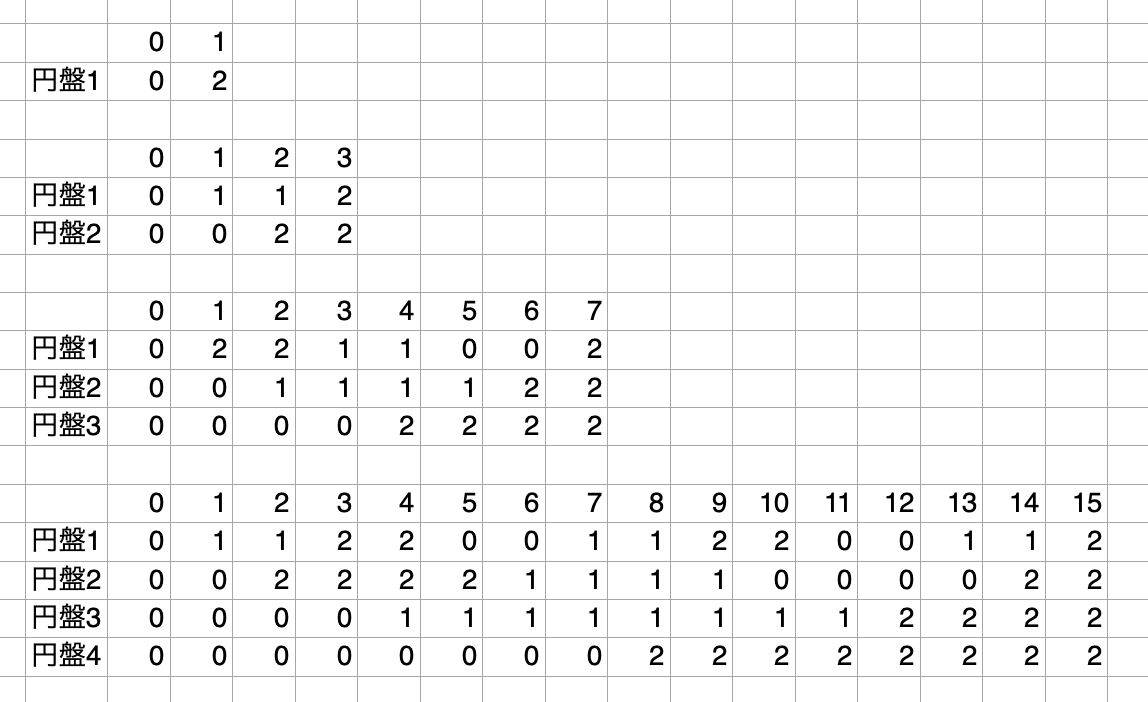
規則性があるということは計算で手順を求めることができるはず!
ということで考えてみました。
- 円盤nは、(2^n-1)-1手目まで移動しない(tower[0]にいる)
- 円盤nは、2^n - 2^(n-1)手で移動が完了する(tower[2]にいる)
- 1.2のどちらにも当てはまらない場合、大きさが2番目以下の円盤nは [1,2,0]または[2,1,0]のパターンから一つが選択され、その要素を2^n回ずつ繰り返す。
パターン選択の規則は
大きさが2番目の円盤は [1,2,0]
大きさが3番目の円盤は [2,1,0]
大きさが4番目の円盤は [1,2,0]
大きさが5番目の円盤は [2,1,0]
・
・
・
となっている。
これらをコードにまとめると以下のようになりました。これで100段ハノイにも対応可能となりました!
def solve(input_lines)
n, t = input_lines.split.map(&:to_i)
pattern = [[2, 1, 0], [1, 2, 0]]
towers = Array.new(3) { [] }
(1..n).reverse_each.with_index do |disk, i|
k = 2 ** (disk - 1)
if t < k
towers[0] << disk
elsif t >= 2 ** n - k
towers[2] << disk
else
towers[pattern[i % 2][((t - k) / 2 ** disk) % 3]] << disk
end
end
towers.map do |disks|
disks.empty? ? "-" : disks.join(" ")
end
end
puts solve(STDIN.read)
今回のまとめ
- ハノイの塔を解く最少手数は 2^n-1 回 (n: 円盤の数)
- n-1番までの円盤を杭Aから杭Bに移動させる: 2^(n-1) - 1 回
- n番の円盤を杭Aから杭Bに移動させる: 1回
- n-1番までの円盤を杭Bから杭Cに移動させる: 2^(n-1) - 1 回
- ハノイの塔は再帰呼び出しを使うことで簡単に求めることができる

ハノイの塔は再帰を理解するのに良い問題ですね!




