こんにちは!じゃいごテックのあつしです。
今回はpaiza DPメニュー 「セクション2【階段の上り方】 STEP1, 2, FINAL」 を解説します。
この問題集は動的計画法(Dynamic Programming, DP)に関する6個のセクションで構成されています。
各セクションにはそれぞれ複数のSTEP問題とFINAL問題があり、STEP問題を解いていけばFINAL問題も解けるはず!となっています。
STEP問題 を解いてみる
簡単な解説は付けていますが、難しいと感じたら下記の記事も参考にしてみて下さい。
分割統治法・動的計画法
メソッドの定義と呼び出し
標準入力・標準出力
STEP1: 階段の上り方 1 (paizaランク B 相当)
整数nが与えられ、階段を上るのに1 歩で 1 段、または 1歩で2 段を上ることができるとき、n 段の階段を上る方法は何通りあるかを答える問題です。
漸化式
- a_n = a_{n-2} + a_{n-1} (n ≧ 3)
(1段前、2段前から上る2通りある)
解答例
INPUT1 = <<~"EOS"
3
EOS
OUTPUT1 = <<~"EOS"
3
EOS
def solve(input_data)
n = input_data.to_i
# dpテーブル初期化
# 0段目には上らなくても到達できる
dp = [1] + [0] * n
# dpテーブル更新
1.upto(n) do |i|
# i-1 段目から1段上って i 段へ到達
dp[i] += dp[i - 1] if i >= 1
# i-2 段目から2段上って i 段へ到達
dp[i] += dp[i - 2] if i >= 2
end
# n 段目に行く経路数を返す
dp[n]
end
puts solve(STDIN.read)
# 確認用コード
# puts solve(INPUT1)
# > 3
整数nを受け取る。dpに[1] + [0] * nを代入する。
(dp[0]~[n+1] = 0で初期化後dp[0] = 1代入と同じ)i = 1 ~ nで繰り返し処理を設定する。- i >= 1 のとき、dp[i] += dp[i - 1]
(i段目へ行ける経路数に、1段前へ行ける経路数を加える) - i >= 2 のとき、dp[i] += dp[i - 2]
(i段目へ行ける経路数に、2段前へ行ける経路数を加える)
- i >= 1 のとき、dp[i] += dp[i - 1]
dp[n]にn段目に行ける経路の数が入っているので返す。
(dp[0]: 0段目, dp[1]: 1段目, dp[2]: 2段目, ..., dp[n]: n段目)
入出力例1の処理
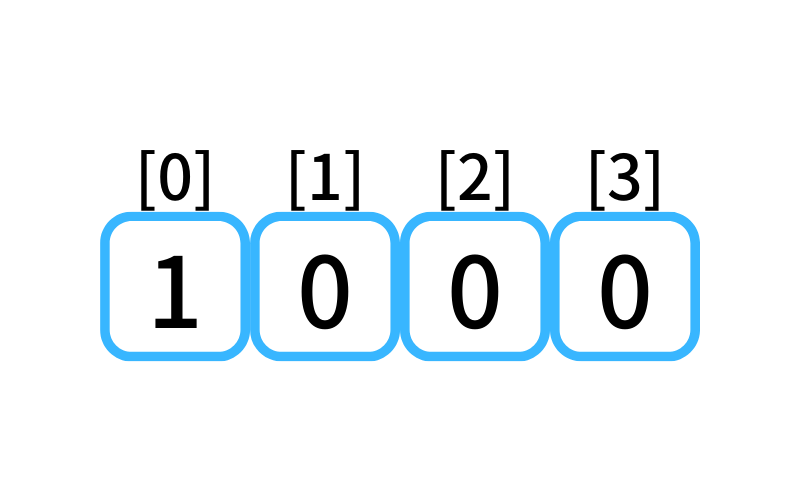
dpテーブルを初期化した状態。
上らなくても0段目に行ける。
ここからi = 1 ~ 3のループ
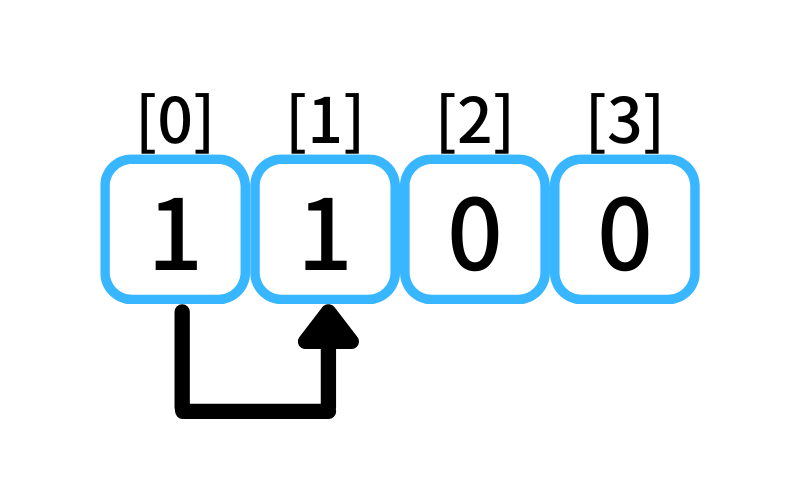
i = 1 : 1段目に行く経路
- 0段目から1段を1歩で上る
0段目に上る経路数は1なので、
1段目に行ける経路数は1。
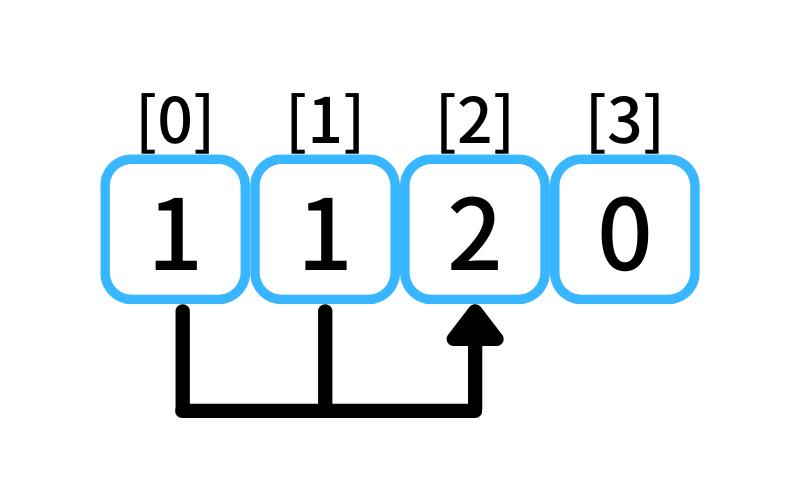
i = 2 : 2段目に行く経路
- 1段目から1段を1歩で上る
- 0段目から2段を1歩で上る
0段目に上る経路数は1、
1段目に上る経路数は1なので、
2段目に行ける経路数は2。
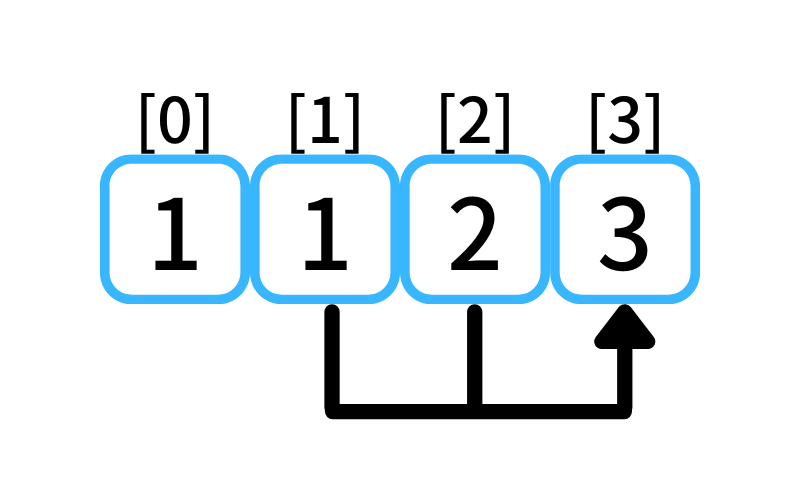
i = 3 : 3段目に行く経路
- 2段目から1段を1歩で上る
- 1段目から2段を1歩で上る
1段目に上る経路数は1、
2段目に上る経路数は2なので、
3段目に行ける経路数は3。
STEP2: 階段の上り方 2 (paizaランク B 相当)
整数n, a, bが与えられ、階段を上るのに1 歩で a段、または b 段を上ることができるとき、n 段の階段を上る方法は何通りあるかを答える問題です。
漸化式
- a_n = a_{n-a}(n ≧ a) + a_{n-b}(n ≧ a) (a段前、b段前から1歩で上る2通りある)
解答例
INPUT1 = <<~"EOS"
11 3 4
EOS
OUTPUT1 = <<~"EOS"
3
EOS
def solve(input_data)
n, a, b = input_data.split.map(&:to_i)
# dpテーブル初期化
# 0段目には上らなくても到達できる
dp = [1] + [0] * n
# dpテーブル更新
1.upto(n) do |i|
# i-a 段目から a 段上って i 段へ到達
dp[i] += dp[i - a] if i >= a
# i-b 段目から b 段上って i 段へ到達
dp[i] += dp[i - b] if i >= b
end
# n 段目に行く経路数を返す
dp[n]
end
puts solve(STDIN.read)
# 確認用コード
# puts solve(INPUT1)
# > 3
STEP1と同様の処理で解くことができます。
整数nを受け取る。dpに[1] + [0] * nを代入する。
(dp[0]~[n+1] = 0で初期化後dp[0] = 1代入と同じ)i = 1 ~ nで繰り返し処理を設定する。- i >= a のとき、dp[i] += dp[i - a]
(i段目へ行ける経路数に、a段前へ行ける経路数を加える) - i >= b のとき、dp[i] += dp[i - b]
(i段目へ行ける経路数に、b段前へ行ける経路数を加える)
- i >= a のとき、dp[i] += dp[i - a]
dp[n]にn段目に行ける経路の数が入っているので返す。
(dp[0]: 0段目, dp[1]: 1段目, dp[2]: 2段目, ..., dp[n]: n段目)
入出力例1の処理
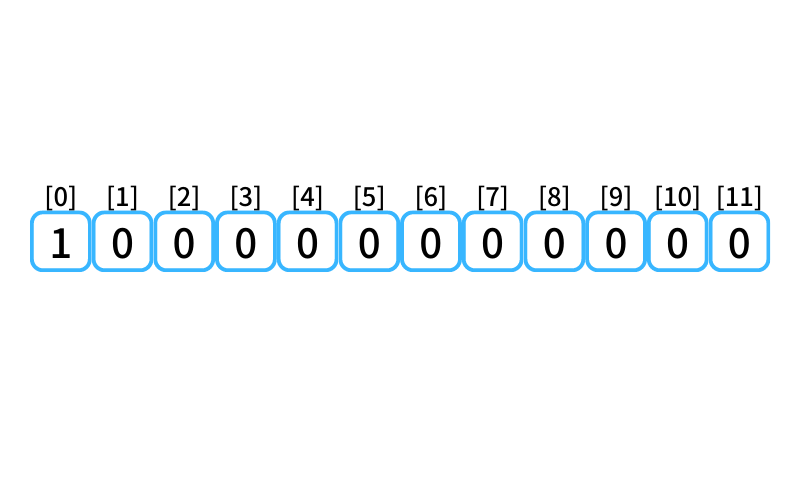
dpテーブルを初期化した状態。
上らなくても0段目に行ける。
ここからi = 1 ~ 11のループ

i = 1, 2 : 1, 2段目に行く経路
i < 3, i <4 なので、
1、2段目に行ける経路数は0。
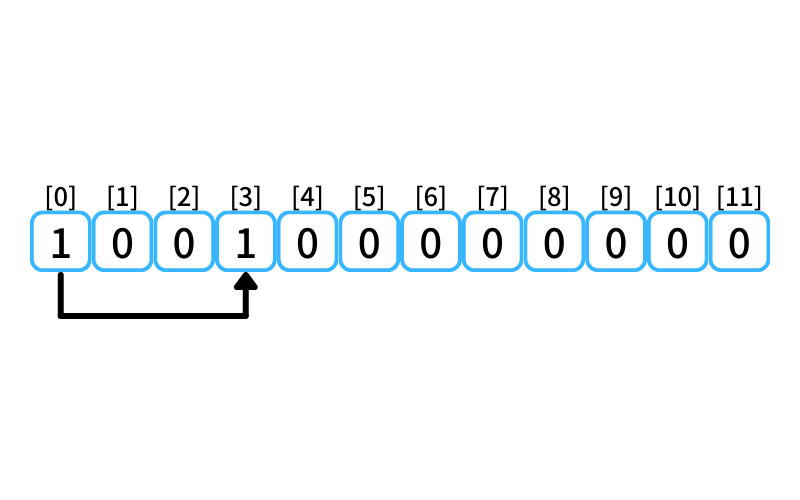
i = 3 : 3段目に行く経路
- 0段目から3段を1歩で上る
0段目に上る経路数は1なので、
3段目に行ける経路数は1。
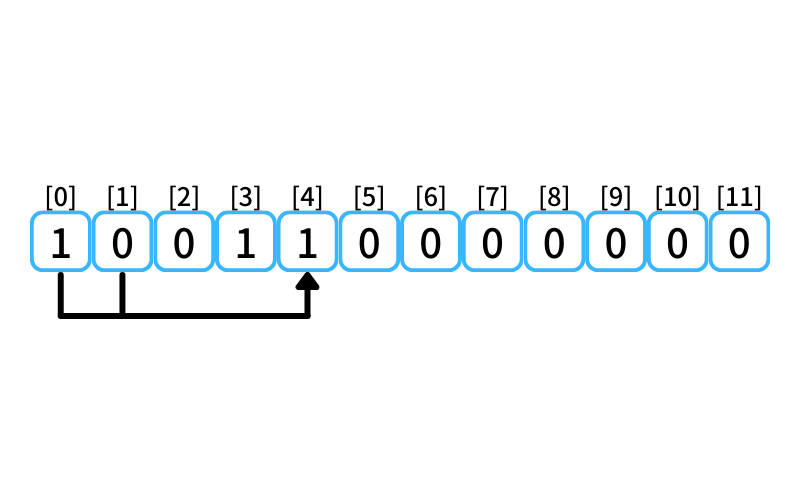
i = 4 : 4段目に行く経路
- 1段目から3段を1歩で上る
- 0段目から4段を1歩で上る
0段目に上る経路数は1、
1段目に上る経路数は0なので、
4段目に行ける経路数は1。
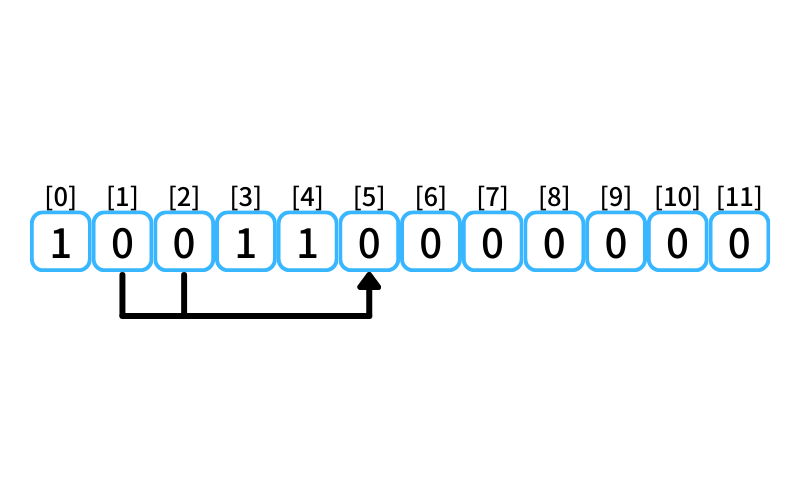
i = 5 : 5段目に行く経路
- 2段目から3段を1歩で上る
- 1段目から4段を1歩で上る
0段目に上る経路数は0、
1段目に上る経路数は0なので、
5段目に行ける経路数は0。
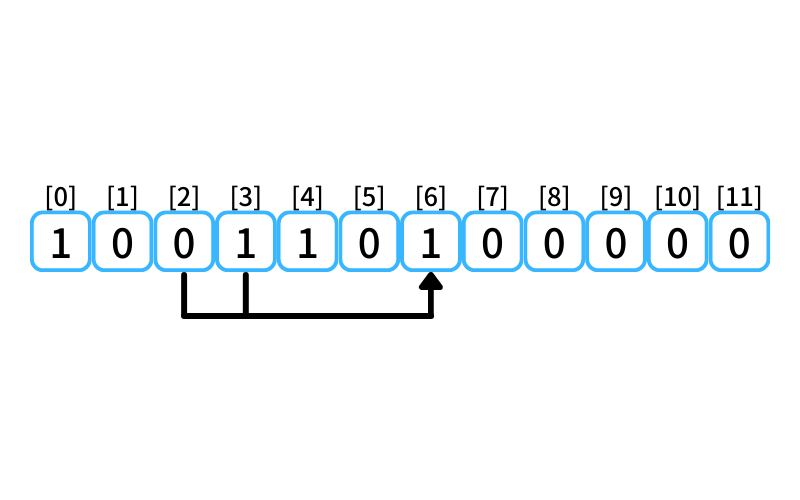
i = 6 : 6段目に行く経路
- 3段目から3段を1歩で上る
- 2段目から4段を1歩で上る
2段目に上る経路数は0、
3段目に上る経路数は1なので、
6段目に行ける経路数は1。
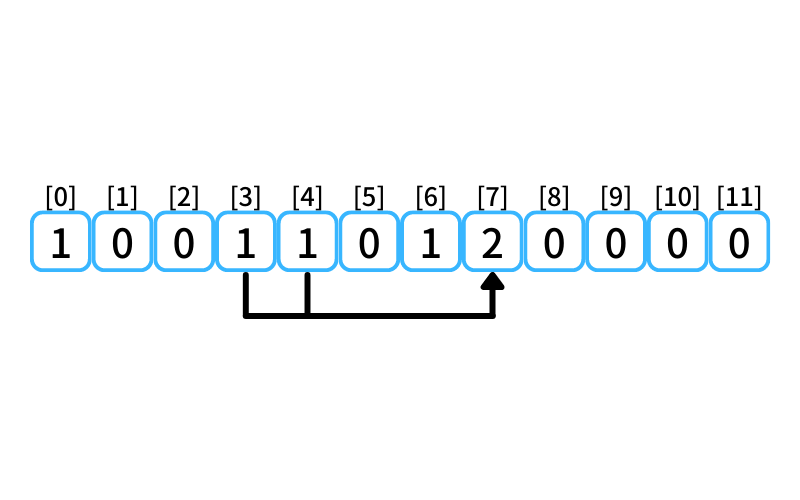
i = 7 : 7段目に行く経路
- 4段目から3段を1歩で上る
- 3段目から4段を1歩で上る
3段目に上る経路数は1、
4段目に上る経路数は1なので、
7段目に行ける経路数は2。
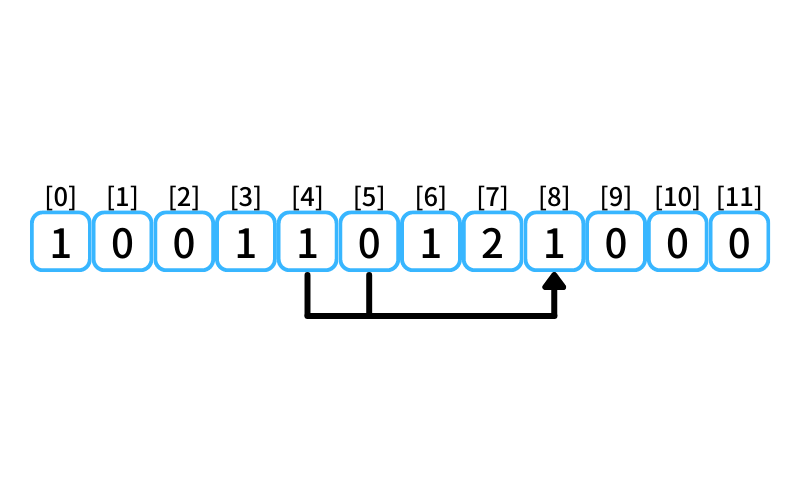
i = 8 : 8段目に行く経路
- 5段目から3段を1歩で上る
- 4段目から4段を1歩で上る
4段目に上る経路数は1、
5段目に上る経路数は0なので、
8段目に行ける経路数は1。
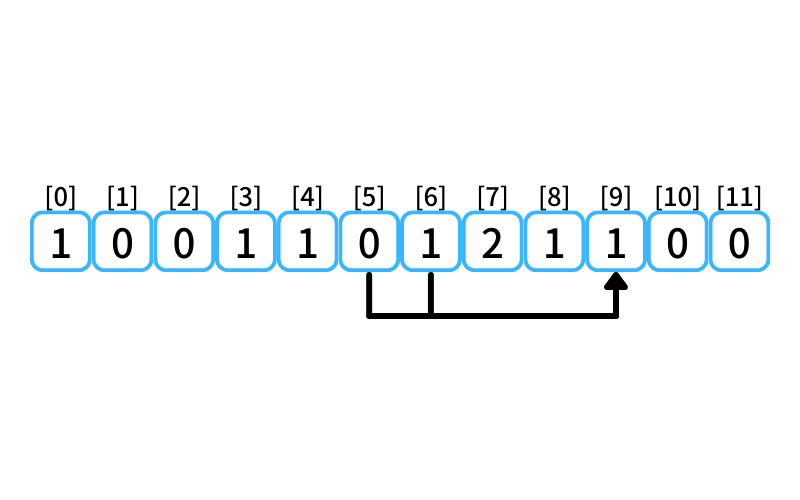
i = 9 : 9段目に行く経路
- 6段目から3段を1歩で上る
- 5段目から4段を1歩で上る
5段目に上る経路数は0、
6段目に上る経路数は1なので、
9段目に行ける経路数は1。
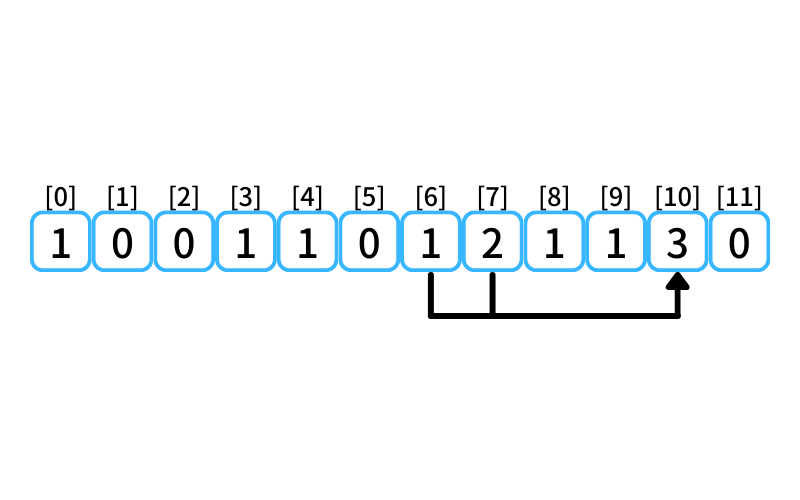
i = 10 : 10段目に行く経路
- 7段目から3段を1歩で上る
- 6段目から4段を1歩で上る
6段目に上る経路数は1、
7段目に上る経路数は2なので、
10段目に行ける経路数は3。
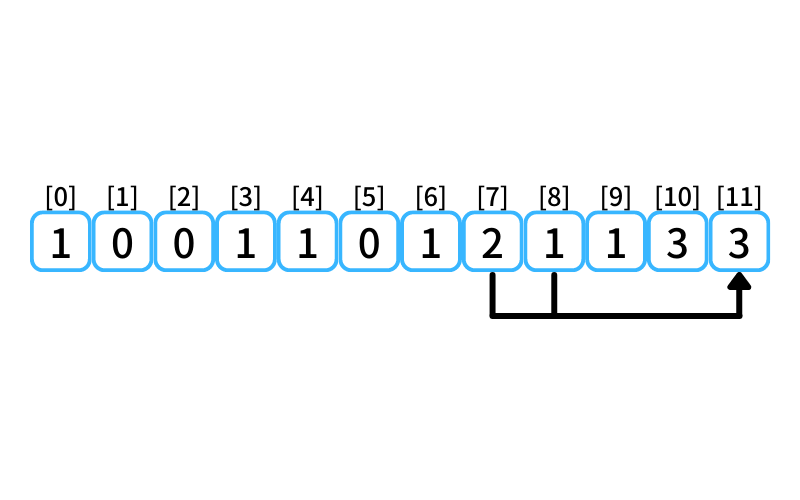
i = 11 : 11段目に行く経路
- 8段目から3段を1歩で上る
- 7段目から4段を1歩で上る
7段目に上る経路数は2、
8段目に上る経路数は1なので、
11段目に行ける経路数は3。
FINAL問題: 階段の上り方 3 (paizaランク B 相当)
※ paizaレベルアップ問題集 DPメニューより
問題
整数 n, a, b, c が与えられます。
階段を上るのに、1歩で a 段または b 段または c 段を上ることができるとき、n 段の階段を上る方法は何通りあるでしょうか。
(ヒント)
上り方が2つから3つへ増えましたが、やることは同じです。
入力される値
n a b c
入力値最終行の末尾に改行が1つ入ります。
期待する出力
n 段の階段を上る方法の数を1行に出力してください。
また、末尾に改行を入れ、余計な文字、空行を含んではいけません。
条件
すべてのテストケースにおいて、以下の条件をみたします。
- 1 ≦ n ≦ 30
- 1 ≦ a ≦ 7
- 1 ≦ b ≦ 7
- 1 ≦ c ≦ 7
- a ≠ b
- b ≠ c
- c ≠ a
- 入力例1
- 10 2 3 4
- 出力例1
- 17
攻略ポイント
ポイント
- 漸化式を立てて問題を解く。
問題を解く流れ
入出力例をコピペしてヒアドキュメントで変数に代入し、データを確認します。正しく受け取れていれば確認用コードは削除します。
INPUT1 = <<~"EOS" 10 2 3 4 EOS OUTPUT1 = <<~"EOS" 17 EOS # 確認用コード p INPUT1 # > "10 2 3 4\n" p OUTPUT1 # > "17\n"
続いて、問題を解くsolveメソッドを変数の下に定義し、入力データを受け取る処理を書きます。
def solve(input_data) n, a, b, c = input_data.split.map(&:to_i) [n, a, b, c] end p solve(INPUT1) # > [10, 2, 3, 4]
データが正しく受け取れていれば、solve メソッドに処理を追加していきます。
- dp = [1] + [0] * nでdpテーブルを初期化する。
i = 1 ~ nの繰り返し処理を設定する。- i >= a のとき、dp[i] += dp[i - a]
(i段目へ行ける経路数に、a段前へ行ける経路数を加える) - i >= b のとき、dp[i] += dp[i - b]
(i段目へ行ける経路数に、b段前へ行ける経路数を加える) - i >= c のとき、dp[i] += dp[i - c]
(i段目へ行ける経路数に、c段前へ行ける経路数を加える) dp[n]にn段目に行ける経路の数が入っているので返す。
(dp[0]: 0段目, dp[1]: 1段目, dp[2]: 2段目, ..., dp[n]: n段目)
- i >= a のとき、dp[i] += dp[i - a]
def solve(input_data)
n, a, b, c = input_data.split.map(&:to_i)
# dpテーブル初期化
# 0段目には上らなくても到達できる
dp = [1] + [0] * n
# dpテーブル更新
1.upto(n) do |i|
# i-a 段目から a 段上って i 段へ到達
dp[i] += dp[i - a] if i >= a
# i-b 段目から b 段上って i 段へ到達
dp[i] += dp[i - b] if i >= b
# i-c 段目から c 段上って i 段へ到達
dp[i] += dp[i - c] if i >= c
end
# n 段目に行く経路数を返す
dp[n]
end
# 確認用コード
puts solve(INPUT1)
# > 17
puts solve(INPUT1) == OUTPUT1
# > false
あとは出力形式を整えれば完成です。
このまま提出しても正解となりますが、p solve(INPUT1) == OUTPUT1 -> true を確認するために、出力を文字列に変換して末尾に改行を加えます。
def solve(input_data)
n, a, b, c = input_data.split.map(&:to_i)
# dpテーブル初期化
# 0段目には上らなくても到達できる
dp = [1] + [0] * n
# dpテーブル更新
1.upto(n) do |i|
# i-a 段目から a 段上って i 段へ到達
dp[i] += dp[i - a] if i >= a
# i-b 段目から b 段上って i 段へ到達
dp[i] += dp[i - b] if i >= b
# i-c 段目から c 段上って i 段へ到達
dp[i] += dp[i - c] if i >= c
end
# n 段目に行く経路数を返す
dp[n].to_s << "\n"
end
# 確認用コード
puts solve(INPUT1)
# > 17
puts solve(INPUT1) == OUTPUT1
# > true
入出力例での動作確認が出来ましたので、標準入力からのデータ受け取りに変更して、手動で動作確認をしたら提出します。
複数行のデータ受け取りなので STDIN.read を使います。(入力終了は Ctrl+D 又は Ctrl+Z)
解答コード
def solve(input_data)
n, a, b, c = input_data.split.map(&:to_i)
# dpテーブル初期化
# 0段目には上らなくても到達できる
dp = [1] + [0] * n
# dpテーブル更新
1.upto(n) do |i|
# i-a 段目から a 段上って i 段へ到達
dp[i] += dp[i - a] if i >= a
# i-b 段目から b 段上って i 段へ到達
dp[i] += dp[i - b] if i >= b
# i-c 段目から c 段上って i 段へ到達
dp[i] += dp[i - c] if i >= c
end
# n 段目に行く経路数を返す
dp[n].to_s << "\n"
end
puts solve(STDIN.read)
入出力例1の処理
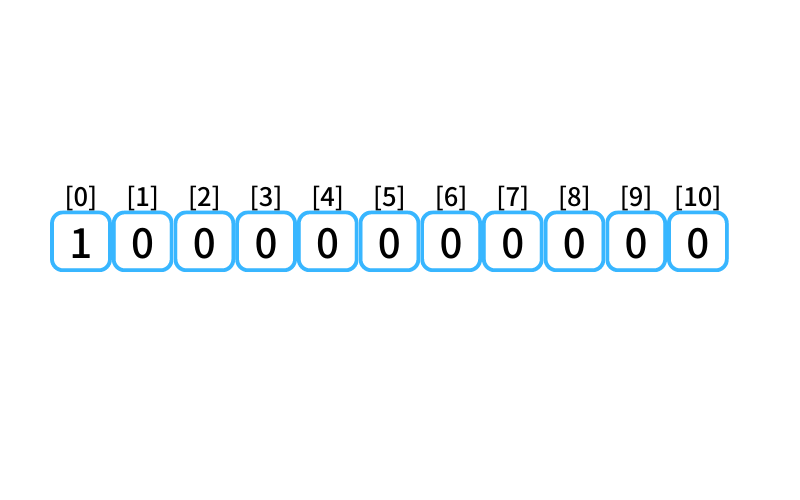
dpテーブルを初期化した状態。
上らなくても0段目に行ける。
ここからi = 1 ~ 10のループ

i = 1 : 1段目に行く経路
i < 2, i < 3, i <4 なので、
1段目に行ける経路数は0。
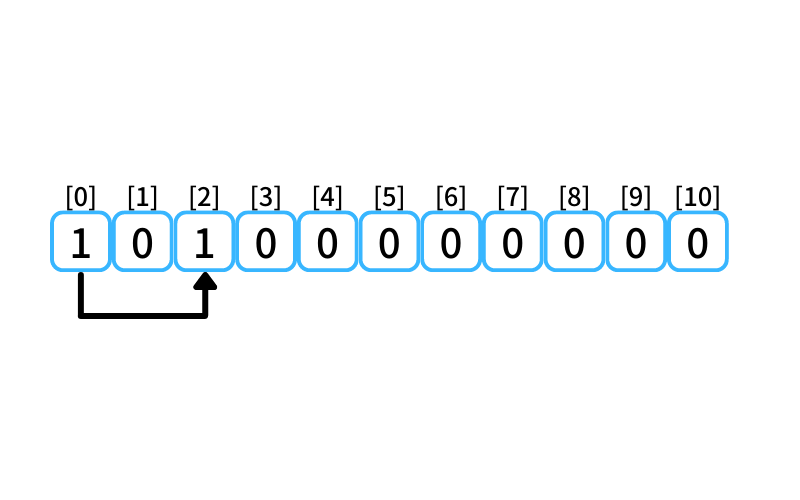
i = 2 : 2段目に行く経路
- 0段目から2段を1歩で上る
0段目に上がる経路数は1なので、
2段目に行ける経路数は1。
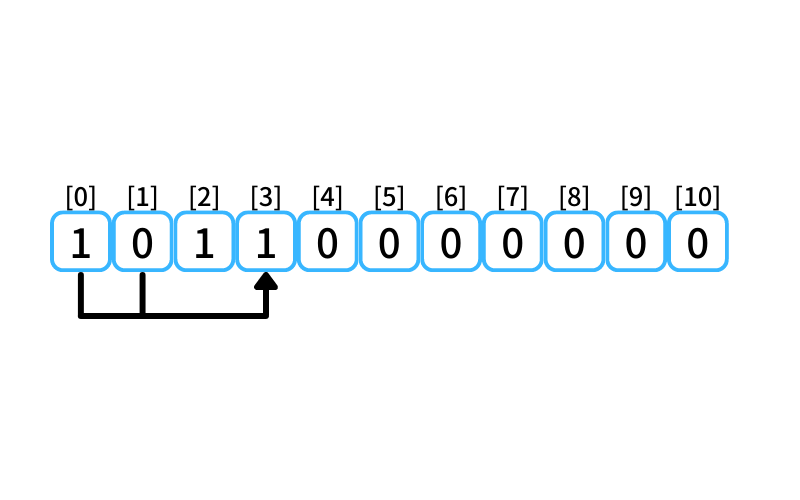
i = 3 : 3段目に行く経路
- 1段目から2段を1歩で上る
- 0段目から3段を1歩で上る
0段目に上る経路数は1、
1段目に上る経路数は0なので、
3段目に行ける経路数は1。
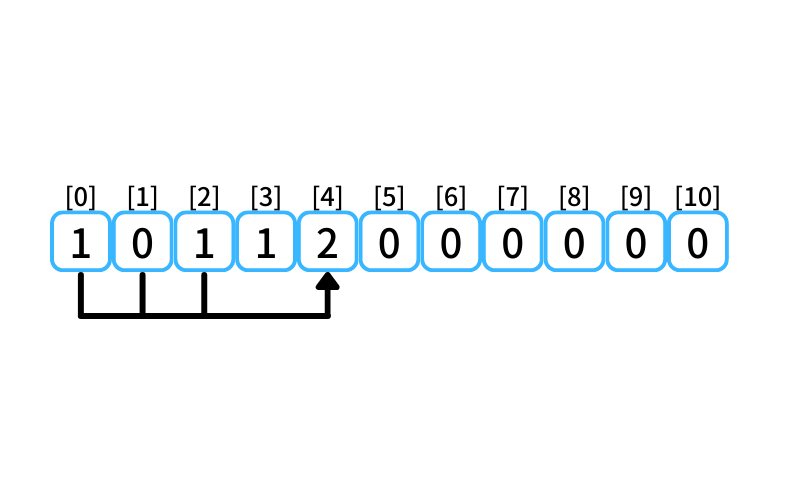
i = 4 : 4段目に行く経路
- 2段目から2段を1歩で上る
- 1段目から3段を1歩で上る
- 0段目から4段を1歩で上る
0段目に上る経路数は1、
1段目に上る経路数は0、
2段目に上る経路数は1なので、
4段目に行ける経路数は2。
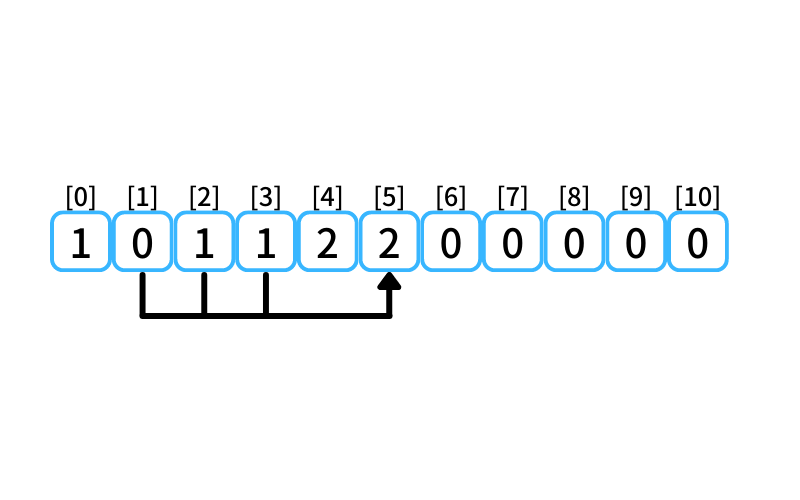
i = 5 : 5段目に行く経路
- 3段目から2段を1歩で上る
- 2段目から3段を1歩で上る
- 1段目から4段を1歩で上る
1段目に上る経路数は0、
2段目に上る経路数は1、
3段目に上る経路数は1なので、
5段目に行ける経路数は2。
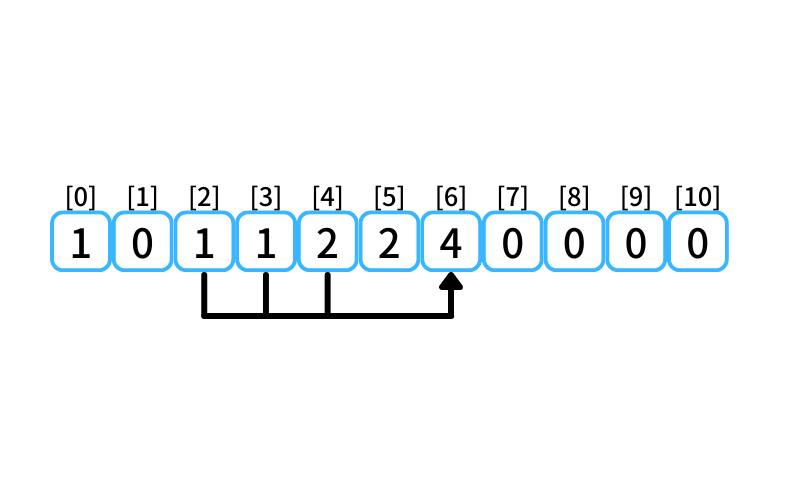
i = 6 : 6段目に行く経路
- 4段目から2段を1歩で上る
- 3段目から3段を1歩で上る
- 2段目から4段を1歩で上る
2段目に上る経路数は1、
3段目に上る経路数は1、
4段目に上る経路数は2なので、
6段目に行ける経路数は4。
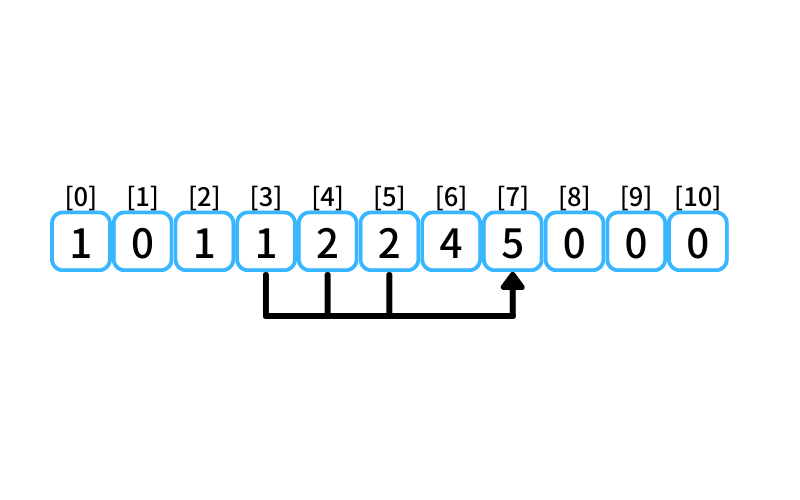
i = 7 : 7段目に行く経路
- 5段目から2段を1歩で上る
- 4段目から3段を1歩で上る
- 3段目から4段を1歩で上る
3段目に上る経路数は1、
4段目に上る経路数は2、
5段目に上る経路数は2なので、
7段目に行ける経路数は5。
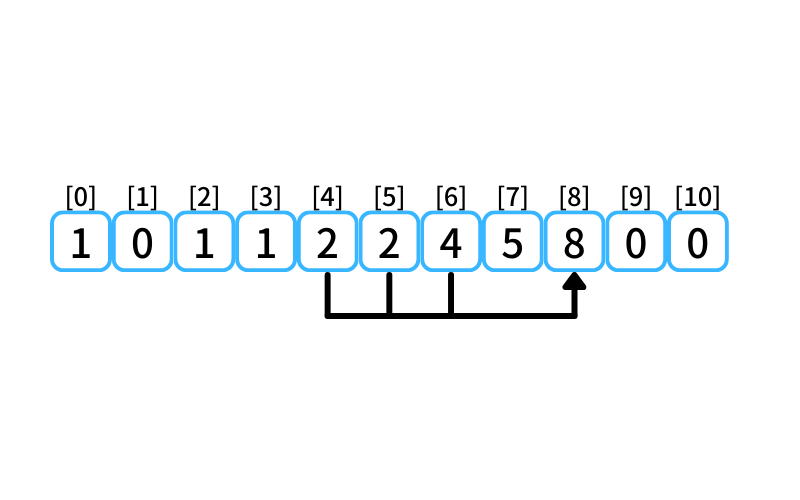
i = 8 : 8段目に行く経路
- 6段目から2段を1歩で上る
- 5段目から3段を1歩で上る
- 4段目から4段を1歩で上る
4段目に上る経路数は2、
5段目に上る経路数は2、
6段目に上る経路数は4なので、
8段目に行ける経路数は8。
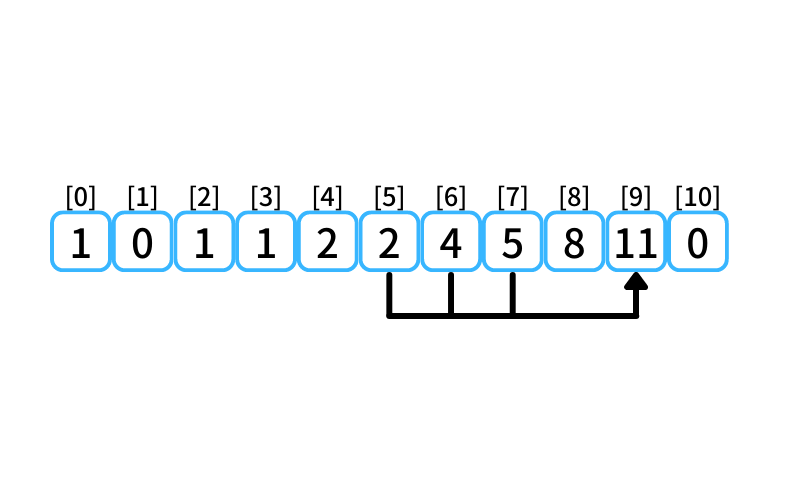
i = 9 : 9段目に行く経路
- 7段目から2段を1歩で上る
- 6段目から3段を1歩で上る
- 5段目から4段を1歩で上る
5段目に上る経路数は2、
6段目に上る経路数は4、
7段目に上る経路数は5なので、
9段目に行ける経路数は11。
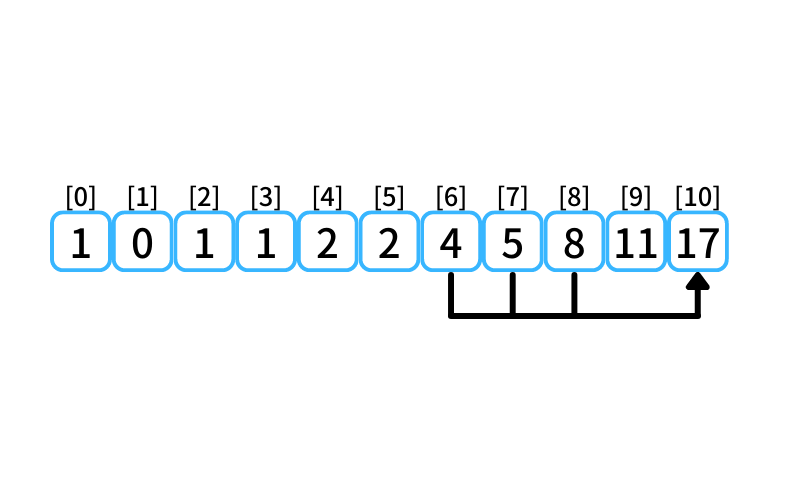
i = 10 : 10段目に行く経路
- 8段目から2段を1歩で上る
- 7段目から3段を1歩で上る
- 6段目から4段を1歩で上る
6段目に上る経路数は4、
7段目に上る経路数は5、
8段目に上る経路数は8なので、
10段目に行ける経路数は17。
今回のまとめ
(ヒントがたくさんありましたけど)セクション2では漸化式を自分で考えて問題を解く課題でした。

dpテーブルの図があるとわかりやすいですね。今回はcanvaで作ってみました。




