paiza プログラミング

[Ruby|Python]paiza リアルイベント問題セット 最小の運賃 (paizaランク A 相当)

paiza解説_最小の運賃

今回はpaiza リアルイベント問題セット 「最小の運賃」 (paizaランク A 相当)を解説します。

0 から v-1 までの駅番号、e個の路線情報（駅aの番号, 駅bの番号, 運賃）、ゴール駅の番号tが与えられたときに、 スタート駅0 から ゴール駅t までの最小運賃を求める、最短経路問題です。

最小の運賃 (paizaランク A 相当)

※ paiza リアルイベント問題セット より

問題

あなたは鉄道での旅行を計画しています。最寄り駅と目的の駅を含む合計 V 箇所の駅があり、どの駅を通過するかによって運賃が変わります。
あなたは旅費の節約のために運賃を最小にしようと考えています。駅と駅の間の運賃が与えられるので目的の駅までの最小運賃を求めてください。
ただし、あなたは常に 0 番目の駅から出発するものとします。

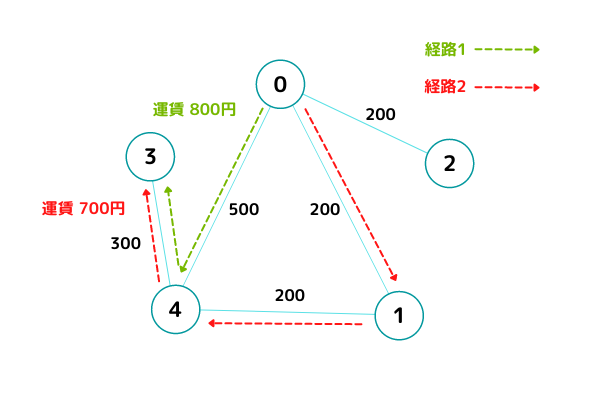
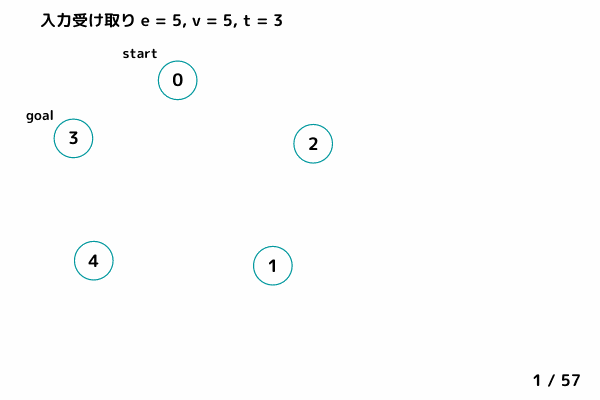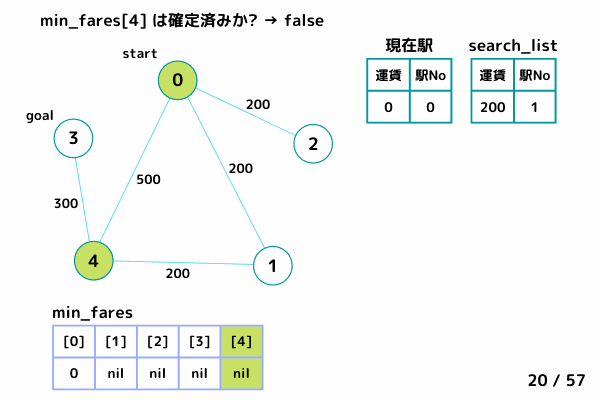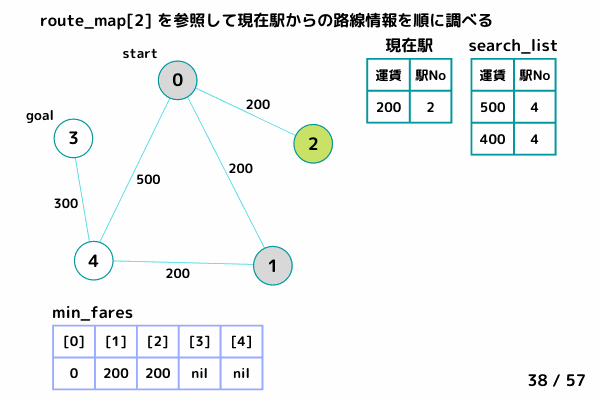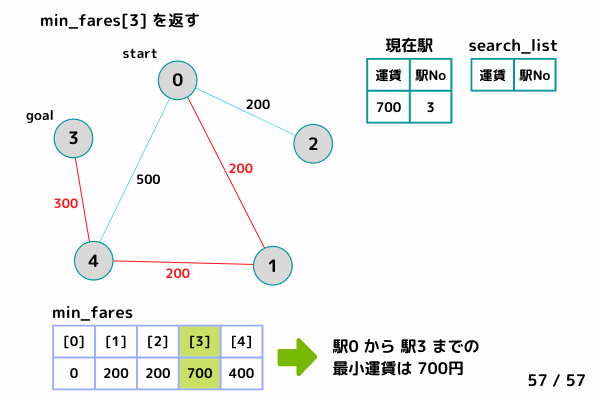
入力例 1 の場合、以下の図のように
0 番目の駅から出発し、4 番目の駅を通り、3 番目の駅に到着すると、800 (500 + 300) 円かかりますが、0 番目、1 番目、4 番目、3 番目の順で 3 番目の駅に向かった場合、700 (200 + 200 + 300) 円になるため、期待される出力は 700 になります。

入力例1の図

入力される値

入力は以下のフォーマットで与えられます。

E V T
s_1 e_1 c_1
s_2 e_2 c_2
...
s_E e_E c_E

  • 1 行目に路線の数 E、全ての駅の数 V、目的地の駅の番号 T が整数でこの順に半角スペース区切りで与えられます。
  • 続く E 行のうちの i 行目 (1 ≦ i ≦ E) には、s_i 番目の駅と e_i 番目駅の間の運賃を表す、c_i がこの順で半角スペース区切りで与えられます。
  • 入力は合計で E + 1 行となり、入力値最終行の末尾に改行が １ つ入ります。

入力値最終行の末尾に改行が１つ入ります。

期待する出力

0 番目の駅から出発し、T 番目の駅に到着する経路の最低運賃を整数で出力してください。

条件

すべてのテストケースにおいて、以下の条件をみたします。

  • 1 ≦ E ≦ 5,000
  • 2 ≦ V ≦ 100
  • 0 ≦ T < V
  • 0 ≦ s_i, e_i < V (1 ≦ i ≦ N)
  • s_i ≠ e_i
  • i ≠ j (1 ≦ i, j ≦ N) ならば、(s_i, e_i) ≠ (s_j, e_j) かつ (s_i, e_i) ≠ (e_j, s_j)
  • 1 ≦ c_i ≦ 1,000 (1 ≦ i ≦ E)
  • 0 番目の駅から T 番目の駅への経路は必ず存在する。
入力例1
5 5 3
0 1 200
0 4 500
0 2 200
1 4 200
4 3 300
出力例1
700
入力例2
3 6 3
0 1 200
1 3 150
2 4 100
出力例2
350
攻略ポイント

ポイント

  • 0 番目の駅から t 番目の駅への経路は必ず存在する。
  • コストが1～1000の正の整数なのでダイクストラ法を使う。

ダイクストラ法

優先度付きキュー

問題を解く流れ

全体の処理を整理する

  • 入力データを受け取る
    • 路線数: 整数e
    • 駅数: 整数v
    • ゴール駅: 整数t
    • 路線情報: routes[駅aの番号, 駅bの番号, 運賃]
  • 路線情報: routes から隣接リストroute_mapを作成する
    • route_map を 要素数vの空のリストで初期化する
    • routesの要素（駅aの番号, 駅bの番号, 運賃）を順に参照する
      駅aの番号: st_a, 駅bの番号: st_b, 運賃: fare

      • route_map[st_a] に [st_b, fare] を追加する（駅aから駅bにfare円で行ける）
      • route_map[st_b] に [st_a, fare] を追加する（駅bから駅aにfare円で行ける）
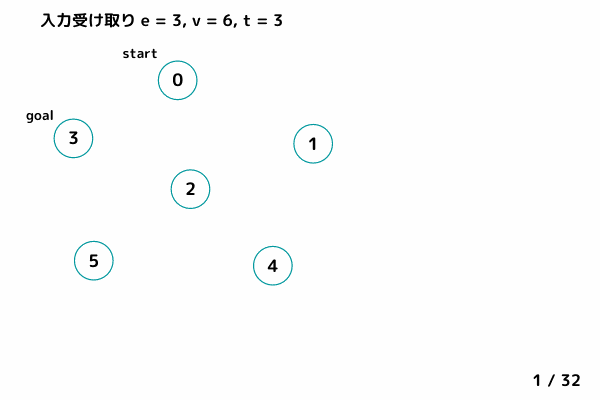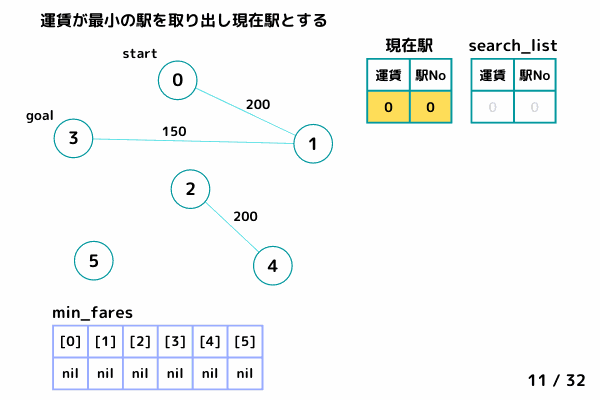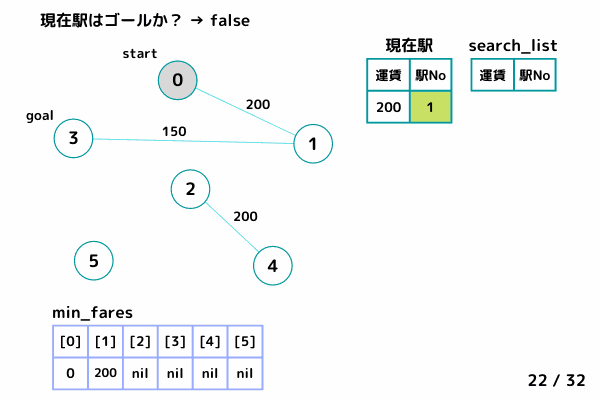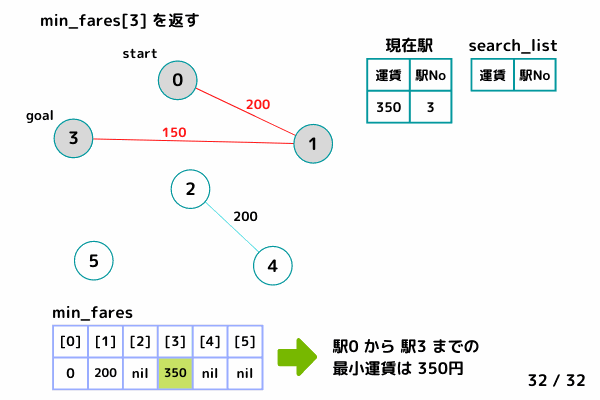
  • 駅0 から 駅t までの最小運賃を求める
    • スタート地点の情報[0: 運賃, 0: 駅番号]で search_list を初期化する
    • 各駅までの最小運賃を nil で初期化する
    • search_list が空になるまで繰り返す
      • search_listから合計運賃が最小の駅を取り出し現在駅とする
        現在駅に着くための運賃: current_fare, 現在駅の番号: current_st
      • 現在駅の最小運賃が確定済みならループをスキップする
      • 現在駅を最小運賃で確定させる
      • 現在駅がゴールなら 駅0 から 駅t までの最小運賃を返す
      • 現在駅からの路線情報を順に調べる
        • 次の駅の最小運賃が確定済みならループをスキップする
        • search_list に次の駅までの運賃と駅番号を追加する

処理の流れはこんな感じです。

INPUT1

min_fare1

INPUT2

min_fare2

Rubyで実装する

入出力例をコピペしてヒアドキュメントで変数に代入し、データを確認します。正しく受け取れていれば確認用コードは削除します。

INPUT1 = <<~"EOS"
  5 5 3
  0 1 200
  0 4 500
  0 2 200
  1 4 200
  4 3 300
EOS
OUTPUT1 = <<~"EOS"
  700
EOS

INPUT2 = <<~"EOS"
  3 6 3
  0 1 200
  1 3 150
  2 4 100
EOS
OUTPUT2 = <<~"EOS"
  350
EOS

# 確認用コード
p INPUT1
# > "5 5 3\n0 1 200\n0 4 500\n0 2 200\n1 4 200\n4 3 300\n"
p OUTPUT1
# > "700\n"
p INPUT2
# > "3 6 3\n0 1 200\n1 3 150\n2 4 100\n"
p OUTPUT2
# > "350\n"

続いて問題を解くメソッド（ solve メソッドとします）を変数の下に定義します。

まず、入力データを受け取る処理を書きます。

def solve(input_str)
  # -----------------------------------
  # 入力受け取り
  # -----------------------------------
  # 入力文字列を改行で分割する
  input_lines = input_str.chomp.split("\n")
  # e: 路線数, v: 駅数, t: 目的地
  e, v, t = input_lines.shift.split.map(&:to_i)
  # routes: 路線の情報
  routes = input_lines.map { |line| line.split.map(&:to_i) }

  # 確認用コード
  [e, v, t, routes]
end

# 確認用コード
p solve(INPUT1)
# > [5, 5, 3, [[0, 1, 200], [0, 4, 500], [0, 2, 200], [1, 4, 200], [4, 3, 300]]]
p solve(INPUT2)
# > [3, 6, 3, [[0, 1, 200], [1, 3, 150], [2, 4, 100]]]

入力データが正しく受けとれていれば、隣接リストroute_map作成処理まで書いて動作を確認します。

def solve(input_str)
  # -----------------------------------
  # 入力受け取り
  # -----------------------------------
  # 入力文字列を改行で分割する
  input_lines = input_str.chomp.split("\n")
  # e: 路線数, v: 駅数, t: 目的地
  e, v, t = input_lines.shift.split.map(&:to_i)
  # routes: 路線の情報
  routes = input_lines.map { |line| line.split.map(&:to_i) }

  # -----------------------------------
  # route_map: 隣接リスト作成
  # -----------------------------------
  route_map = Array.new(v) { [] }
  # st_a: 駅a, st_b: 駅b, fare: 運賃
  routes.each do |st_a, st_b, fare|
    # 駅a と 駅b は同じ運賃で行き来できる
    route_map[st_a] << [st_b, fare]
    route_map[st_b] << [st_a, fare]
  end

  # 確認用コード
  route_map
end

# 確認用コード
p solve(INPUT1)
# > [[[1, 200], [4, 500], [2, 200]], [[0, 200], [4, 200]], [[0, 200]], [[4, 300]], [[0, 500], [1, 200], [3, 300]]]
p solve(INPUT2)
# > [[[1, 200]], [[0, 200], [3, 150]], [[4, 100]], [[1, 150]], [[2, 100]], []]

INPUT1

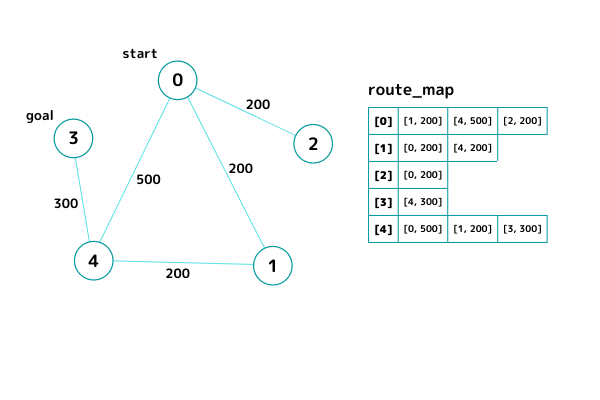
input1_route_map

INPUT2

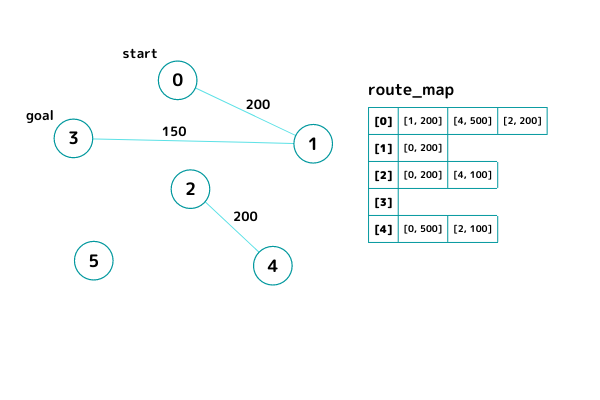
input2_route_map

イメージ通りのroute_mapが作成できました！

続いて、駅0 から 駅t までの最小運賃を求める処理をダイクストラ法で書いていきます。

def solve(input_str)
  # -----------------------------------
  # 入力受け取り
  # -----------------------------------
  # 入力文字列を改行で分割する
  input_lines = input_str.chomp.split("\n")
  # e: 路線数, v: 駅数, t: 目的地
  e, v, t = input_lines.shift.split.map(&:to_i)
  # routes: 路線の情報
  routes = input_lines.map { |line| line.split.map(&:to_i) }

  # -----------------------------------
  # route_map: 隣接リスト作成
  # -----------------------------------
  route_map = Array.new(v) { [] }
  # st_a: 駅a, st_b: 駅b, fare: 運賃
  routes.each do |st_a, st_b, fare|
    # 駅a と 駅b は同じ運賃で行き来できる
    route_map[st_a] << [st_b, fare]
    route_map[st_b] << [st_a, fare]
  end

  # -----------------------------------
  # 駅0 から 駅t までの最小運賃を求める
  # -----------------------------------
  # スタート地点の情報[0: 運賃, 0: 駅番号]で search_list を初期化
  search_list = [[0, 0]]
  # 各駅までの最小運賃を nil で初期化
  min_fares = Array.new(v)
  # search_list が空になるまで繰り返す
  while not search_list.empty?
    # 合計運賃が最小の駅を取り出し現在駅とする
    # current_fare: 現在駅に着くための合計運賃
    # current_st: 現在駅番号
    current_fare, current_st = search_list.sort!.shift
    # 現在駅の最小運賃が確定済みならスキップ
    next if not min_fares[current_st].nil?
    # 現在駅を最小運賃で確定させる
    min_fares[current_st] = current_fare

    # 現在駅がゴールなら駅tまでの最小運賃を返す
    if current_st == t
      return min_fares[t].to_s << "\n"
    end

    # 現在駅からの路線情報を順に調べる
    route_map[current_st].each do |next_st, next_fare|
      # 次の駅の最小運賃が確定済みならスキップ
      next if not min_fares[next_st].nil?
      # search_list に次の駅のまでの運賃と駅番号を追加
      search_list << [current_fare + next_fare, next_st]
    end
  end
end

# 確認用コード
p solve(INPUT1)
# > "700\n"
p solve(INPUT1) == OUTPUT1
# > true
p solve(INPUT2)
# > "350\n"
p solve(INPUT2) == OUTPUT2
# > true

確認用コードを標準入力からのデータ受け取りに変更、標準出力をpメソッドからputsメソッドに変更して提出します。（STDIN.readの入力終了は Ctrl+D)

Ruby 解答コード
def solve(input_str)
  # -----------------------------------
  # 入力受け取り
  # -----------------------------------
  # 入力文字列を改行で分割する
  input_lines = input_str.chomp.split("\n")
  # e: 路線数, v: 駅数, t: 目的地
  e, v, t = input_lines.shift.split.map(&:to_i)
  # routes: 路線の情報
  routes = input_lines.map { |line| line.split.map(&:to_i) }

  # -----------------------------------
  # route_map: 隣接リスト作成
  # -----------------------------------
  route_map = Array.new(v) { [] }
  # st_a: 駅a, st_b: 駅b, fare: 運賃
  routes.each do |st_a, st_b, fare|
    # 駅a と 駅b は同じ運賃で行き来できる
    route_map[st_a] << [st_b, fare]
    route_map[st_b] << [st_a, fare]
  end

  # -----------------------------------
  # 駅0 から 駅t までの最小運賃を求める
  # -----------------------------------
  # スタート地点の情報[0: 運賃, 0: 駅番号]で search_list を初期化
  search_list = [[0, 0]]
  # 各駅までの最小運賃を nil で初期化
  min_fares = Array.new(v)
  # search_list が空になるまで繰り返す
  while not search_list.empty?
    # 合計運賃が最小の駅を取り出し現在駅とする
    # current_fare: 現在駅に着くための合計運賃
    # current_st: 現在駅番号
    current_fare, current_st = search_list.sort!.shift
    # 現在駅の最小運賃が確定済みならスキップ
    next if not min_fares[current_st].nil?
    # 現在駅を最小運賃で確定させる
    min_fares[current_st] = current_fare

    # 現在駅がゴールなら駅tまでの最小運賃を返す
    # (文字列に変換して末尾に改行を追加)
    if current_st == t
      return min_fares[t].to_s << "\n"
    end

    # 現在駅からの路線情報を順に調べる
    route_map[current_st].each do |next_st, next_fare|
      # 次の駅の最小運賃が確定済みならスキップ
      next if not min_fares[next_st].nil?
      # search_list に次の駅のまでの運賃と駅番号を追加
      search_list << [current_fare + next_fare, next_st]
    end
  end
end

puts solve(STDIN.read)
Ruby 別解

search_list に優先度付きキューを使用することで最小コストの要素を出し入れする処理を高速化出来ます。

class PriorityQueue
  def initialize(elements: [], key: 0)
    @data = []
    @key = key
    elements.each { |element| insert(element) }
  end

  def insert(element)
    @data << element
    up_heap
  end

  def extract
    target_element = @data.shift
    if size > 0
      @data.unshift(@data.pop)
      down_heap
    end
    target_element
  end

  def size
    @data.length
  end

  private

  def swap(a, b)
    @data[a], @data[b] = @data[b], @data[a]
  end

  def parent_idx(idx)
    idx / 2 + idx % 2 - 1
  end

  def left_child_idx(idx)
    (idx * 2) + 1
  end

  def right_child_idx(idx)
    (idx * 2) + 2
  end

  def has_child?(idx)
    ((idx * 2) + 1) < size
  end

  def up_heap
    idx = size - 1
    return if idx == 0
    parent_idx = parent_idx(idx)
    while @data[parent_idx][@key] > @data[idx][@key]
      swap(parent_idx, idx)
      return if parent_idx == 0
      idx = parent_idx
      parent_idx = parent_idx(idx)
    end
  end

  def down_heap
    idx = 0
    while (has_child?(idx))
      l_idx = left_child_idx(idx)
      r_idx = right_child_idx(idx)
      if @data[r_idx].nil?
        target_idx = l_idx
      else
        target_idx = @data[l_idx][@key] <= @data[r_idx][@key] ? l_idx : r_idx
      end
      if @data[idx][@key] > @data[target_idx][@key]
        swap(idx, target_idx)
        idx = target_idx
      else
        return
      end
    end
  end
end

def solve(input_str)
  # -----------------------------------
  # 入力受け取り
  # -----------------------------------
  # 入力文字列を改行で分割する
  input_lines = input_str.chomp.split("\n")
  # e: 路線数, v: 駅数, t: 目的地
  e, v, t = input_lines.shift.split.map(&:to_i)
  # routes: 路線の情報
  routes = input_lines.map { |line| line.split.map(&:to_i) }

  # -----------------------------------
  # route_map: 隣接リスト作成
  # -----------------------------------
  route_map = Array.new(v) { [] }
  # st_a: 出発駅, st_b: 到着駅, fare: 運賃
  routes.each do |st_a, st_b, fare|
    # 駅a と 駅b は同じ運賃で行き来できる
    route_map[st_a] << [st_b, fare]
    route_map[st_b] << [st_a, fare]
  end

  # -----------------------------------
  # 駅0 から 駅t までの最小運賃を求める
  # -----------------------------------
  # スタート地点の情報[0: 運賃, 0: 駅番号]で search_list を初期化
  search_list = PriorityQueue.new(elements: [[0, 0]])
  # 各駅までの最小運賃を nil で初期化
  min_fares = Array.new(v)
  # search_list が空になるまで繰り返す
  while search_list.size > 0
    # 合計運賃が最小の駅を取り出し現在駅とする
    # current_fare: 現在駅に着くための運賃
    # current_st: 現在駅の番号
    current_fare, current_st = search_list.extract
    # 現在駅の最小運賃が確定済みならスキップ
    next if not min_fares[current_st].nil?
    # 現在駅を最小運賃で確定させる
    min_fares[current_st] = current_fare

    # 現在駅がゴールなら駅tまでの最小運賃を返す
    # (文字列に変換して末尾に改行を追加)
    if current_st == t
      return min_fares[t].to_s << "\n"
    end

    # 現在駅からの路線情報を順に調べる
    route_map[current_st].each do |next_st, next_fare|
      # 次の駅の最小運賃が確定済みならスキップ
      next if not min_fares[next_st].nil?
      # search_list に次の駅までの運賃と駅番号を追加
      search_list.insert([current_fare + next_fare, next_st])
    end
  end
end

puts solve(STDIN.read)
Python3 解答例

Python3では優先度付きキューのheapqモジュールが標準で用意されています。

import heapq


def solve(input_str):
    # -----------------------------------
    # 入力受け取り
    # -----------------------------------
    # 入力文字列を改行で分割
    input_lines = input_str.strip().split("\n")
    # e: 路線数, v: 駅数, t: 目的地
    e, v, t = map(int, input_lines[0].split())
    # routes: 路線の情報
    routes = [list(map(int, route.split())) for route in input_lines[1:]]

    # -----------------------------------
    # route_map: 隣接リスト作成
    # -----------------------------------
    route_map = [[] for _ in range(v)]
    # st_a: 駅a, st_b: 駅b, fare: 運賃
    for st_a, st_b, fare in routes:
        # 駅a と 駅b は同じ運賃で行き来できる
        route_map[st_a].append([st_b, fare])
        route_map[st_b].append([st_a, fare])

    # -----------------------------------
    # 駅0 から 駅t までの最小運賃を求める
    # -----------------------------------
    # スタート地点の情報[0: 運賃, 0: 駅番号]で search_list を初期化
    search_list = [[0, 0]]
    # 各駅までの最小運賃を None で初期化
    min_fares = [None] * v
    # search_list が空になるまで繰り返す
    while search_list:
        # 合計運賃が最小の駅を取り出し現在駅とする
        # current_fare: 現在駅に着くための合計運賃
        # current_st: 現在駅番号
        current_fare, current_st = heapq.heappop(search_list)
        # 現在駅の最小運賃が確定済みならスキップ
        if min_fares[current_st] is not None:
            continue
        # 現在駅を最小運賃で確定させる
        min_fares[current_st] = current_fare

        # 現在駅がゴールなら駅tまでの最小運賃を返す
        # (文字列に変換して末尾に改行を追加)
        if current_st == t:
            return str(min_fares[t]) + "\n"

        # 現在駅からの路線情報を順に調べる
        for next_st, next_fare in route_map[current_st]:
            # 次の駅の最小運賃が確定済みならスキップ
            if min_fares[next_st] is not None:
                continue
            # search_list に次の駅までの運賃と駅番号を追加
            heapq.heappush(search_list, [current_fare + next_fare, next_st])


print(solve(open(0).read()))
解答例の処理速度比較
Ruby
sortメソッド		 Ruby
優先度付きキュー		 Python3
heapq
テスト1 0.12 0.12 0.03
テスト2 0.13 0.12 0.03
テスト3 0.13 0.12 0.04
テスト4 0.12 0.12 0.03
テスト5 0.14 0.13 0.04
テスト6 0.21 0.13 0.03
テスト7 0.16 0.13 0.03
テスト8 0.25 0.13 0.03

今回のまとめ

今回はダイクストラ法を使って最短経路問題を解きました。

ダイクストラ法はとりあえず使えるようになったかなー。という感じです。
他の最短経路問題アルゴリズム（ベルマンフォード法やワーシャルフロイド法）についても理解を深めていきたいと思います。


【PR】アルゴリズム学習でお世話になった本


アルゴリズム関連の技術書は大抵C/C++で書かれていますが、ある程度プログラムが出来れば、処理の流れは理解することが出来ます。





通称: 螺旋本。C++で解説されています。AOJ(Aizu Online Judge)を運営している会津大学の渡辺准教授が書いた本です。データ構造や計算量の内容から丁寧に書いてありますのでアルゴリズム学習の最初の参考書としてオススメです。


プログラミングコンテスト攻略のためのアルゴリズムとデータ構造 [ 渡部有隆 ]
posted with カエレバ
楽天市場
Amazon
Yahooショッピング




通称: 蟻本。C++で解説されています。競技プログラミング中級者の定番書と言われていて、競技プログラミングで利用できる色々なアルゴリズムを学ぶことが出来ます。かなり高度な内容も含まれているので1冊分を完全に理解するのにはかなりの時間がかかりそうですが、手元に置いて何度も読み返しています。


プログラミングコンテストチャレンジブック第2版 問題解決のアルゴリズム活用力とコーディングテクニッ [ 秋葉拓哉 ]
posted with カエレバ
楽天市場
Amazon
Yahooショッピング




通称: チーター本。C#, C++, JAVAでTopcoderの問題を解説しています。初心者～中級者向けに書かれているので解説が非常に丁寧です。


最強最速アルゴリズマー養成講座 プログラミングコンテストTopCoder攻略ガイド【電子書籍】[ 高橋 直大 ]
posted with カエレバ
楽天市場
Amazon
Yahooショッピング




Python3でアルゴリズムを解説している本です。講義スタイルの本で、図やフローチャートを使ってアルゴリズムとデータ構造についてしっかりと説明されています。代わりにコードは少なめです。Pythonコードが読めなくても十分理解できると思います。


Pythonで体験してわかるアルゴリズムとデータ構造 [ 西澤 弘毅 ]
posted with カエレバ
楽天市場
Amazon
Yahooショッピング

-paiza, プログラミング
-, ,

© 2025 じゃいごテック