こんにちは!じゃいごテックのあつしです。
今回はpaiza DPメニュー 「セクション3【最安値】 STEP1~3, FINAL」 を解説します。
DPメニューは動的計画法(Dynamic Programming, DP)に関する6個のセクションで構成されています。
セクション3【最安値】は入り数と価格が異なるりんごを必要数購入するときの最安値を求める問題です。
STEP問題 を解いてみる
簡単な解説は付けていますが、難しいと感じたら下記の記事も参考にしてみて下さい。
分割統治法・動的計画法
メソッドの定義と呼び出し
標準入力・標準出力
STEP1: 最安値を達成するには 1 (paizaランク B 相当)
りんご1個が a 円で、りんご2個が b 円のとき、n 個のりんごを手に入れるための最安値を求める問題です。
(最安値ならりんごがn個以上になっても良い)
漸化式
- dp[0] = 0
- dp[1] = a
- dp[n] = min(dp[n-1] + a, dp[n-2] + b)(2≦n)
(2個以上は購入数n個にするために1個と2個買う場合で安い方を選ぶ)
解答例
INPUT1 = <<~"EOS"
5 100 150
EOS
OUTPUT1 = <<~"EOS"
400
EOS
def solve(input_data)
n, a, b = input_data.split.map(&:to_i)
# dpテーブル初期化
# 0 個購入: 0 円, 1 個購入: a 円
dp = [0, a]
# dpテーブル更新
2.upto(n) do |i|
dp << [dp[i - 1] + a, dp[i - 2] + b].min
end
# n 個購入時の最安値を返す
dp[n]
end
puts solve(STDIN.read)
# 確認用コード
# puts solve(INPUT1)
# > 400
整数n, a, bを受け取る。dpに[0, a]を代入する。
(0個の最安値は0円、1個の最安値はa円)i = 2 ~ nで繰り返し処理を設定する。- dp << [dp[i - 1] + a, dp[i - 2] + b].min
(dp[i-1]に1個追加した価格とdp[i-2]に2個追加した価格を比べて安い方をdp[i]に記録する)
- dp << [dp[i - 1] + a, dp[i - 2] + b].min
dp[n]にn個購入時の最安値が記録されているので返す。
入出力例1の処理
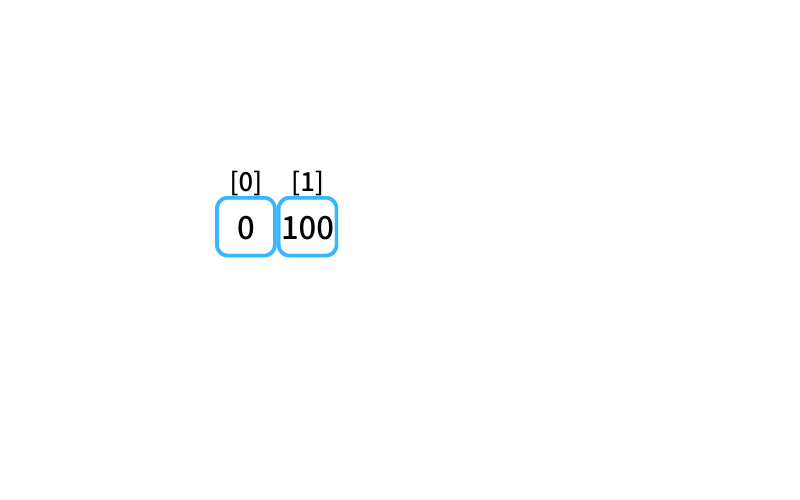
dpテーブルを初期化した状態。
0個買うときの最安値は0円
1個買うときの最安値は100円
ここからi = 2~ 5のループ
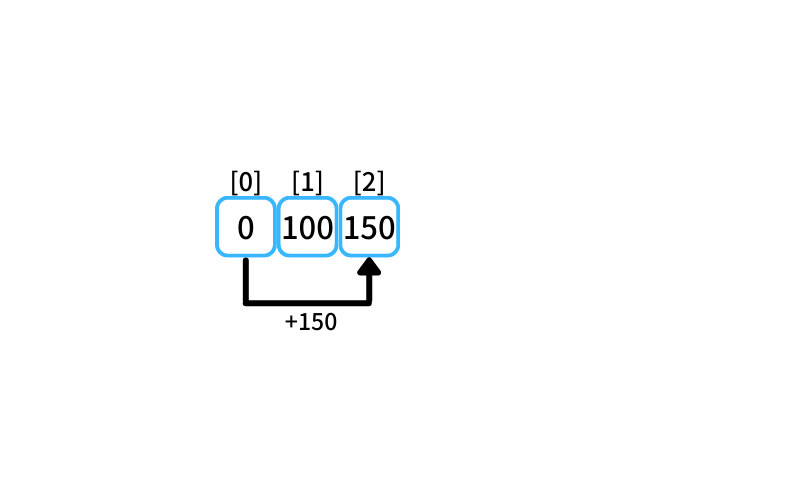
i = 2 : 2個買うときの最安値
- 1個の最安値に1個追加購入
100 + 100 = 200 - 0個の最安値に2個追加購入
0 + 150 = 150
2個買うときの最安値は150円
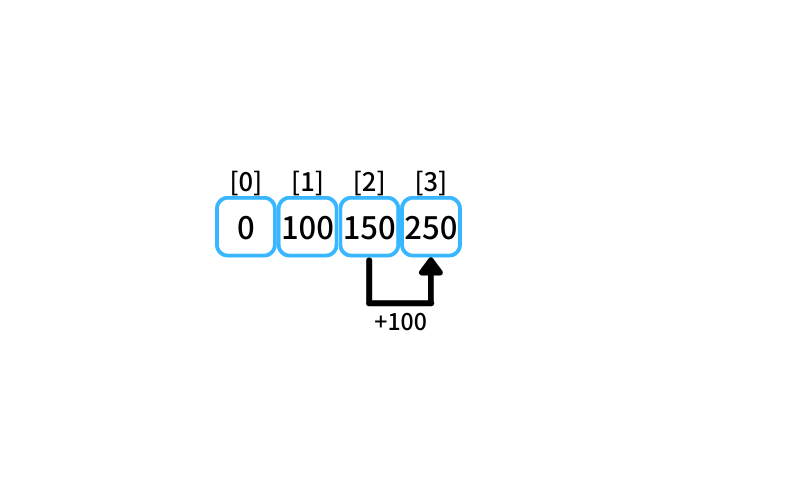
i = 3 : 3個買うときの最安値
- 2個の最安値に1個追加購入
150 + 100 = 250 - 1個の最安値に2個追加購入
100 + 150 = 250
3個買うときの最安値は250円
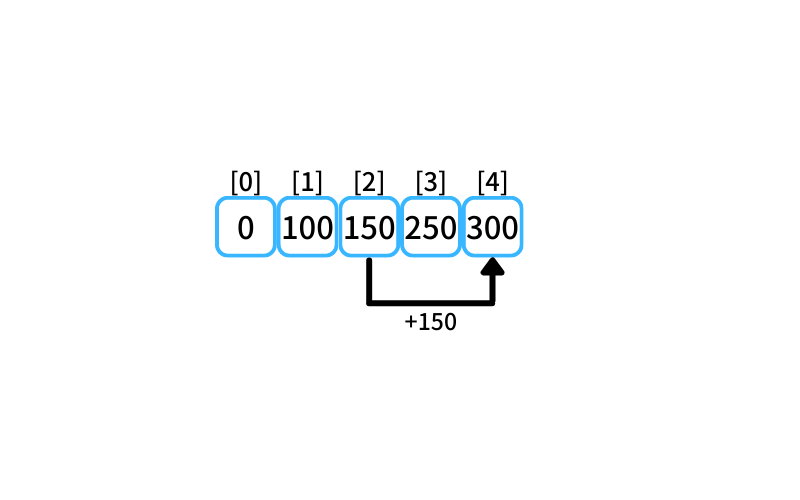
i = 4 : 4個買うときの最安値
- 3個の最安値に1個追加購入
250 + 100 = 350 - 2個の最安値に2個追加購入
150 + 150 = 300
4個買うときの最安値は300円
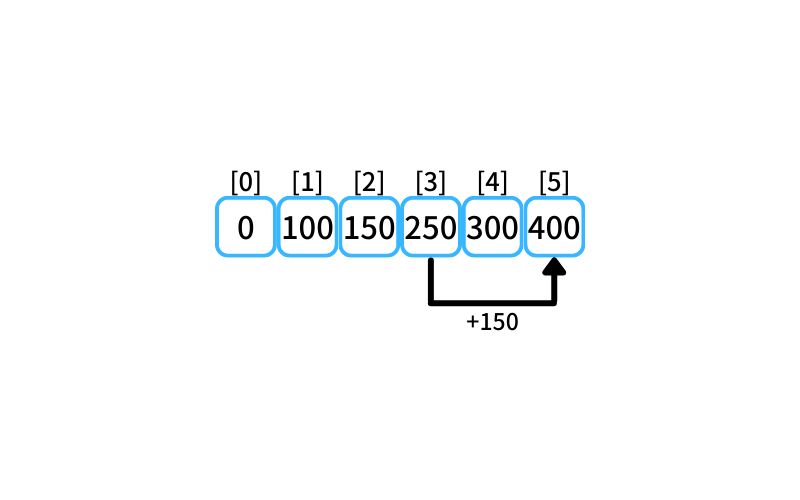
i = 5 : 5個買うときの最安値
- 4個の最安値に1個追加購入
300 + 100 = 400 - 3個の最安値に2個追加購入
250 + 150 = 400
5個買うときの最安値は400円
STEP2: 最安値を達成するには 2 (paizaランク B 相当)
りんご2個が a 円で、りんご5個が b 円のとき、n 個のりんごを手に入れるための最安値を求める問題です。
(最安値ならりんごがn個以上になっても良い)
漸化式
- dp
- dp[i] = 0 (i = 0)
- dp[i] = [dp_a[i], dp_b[i]].min (0 < i)
(2個と5個購入した最安値のうち安い方を記録)
- dp_a (2個購入した場合の最安値)
- dp_a[i] = a (i ≦ 2)
- dp_a[i] = dp[i - 2] + a (2 < i)
- dp_b (5個購入した場合の最安値)
- dp_b[i] = b (i ≦ 5)
- dp_b[i] = dp[i - 5] + a (5 < i)
解答例
INPUT1 = <<~"EOS"
4 110 200
EOS
OUTPUT1 = <<~"EOS"
200
EOS
def solve(input_data)
n, a, b = input_data.split.map(&:to_i)
# dpテーブル初期化
# 0 個購入: 0 円
dp = [0]
# dpテーブル更新
1.upto(n + 4) do |i|
dp_a = i > 2 ? dp[i - 2] + a : a
dp_b = i > 5 ? dp[i - 5] + b : b
# 2個買った場合と5個買った場合で安い方を記録する
dp << [dp_a, dp_b].min
end
# n 個以上購入時の最安値を返す
dp[n..].min
end
puts solve(STDIN.read)
# 確認用コード
# puts solve(INPUT1)
# > 200
整数n, a, bを受け取る。dpに[0]を代入する。(0個の最安値は0円)i = 1 ~ n + 4で繰り返し処理を設定する。
(n個丁度買うときより多く買った方が安い場合があるので多めに(n+4個まで)調べる)- dp_a = i > 2 ? dp[i - 2] + a : a
(2個入りを買ってi個(以上)にした場合の価格をdp_aとする) - dp_b = i > 5 ? dp[i - 5] + b : b
(5個入りを買ってi個(以上)にした場合の価格をdp_bとする) - dp << [dp_a, dp_b].min
(2個入りを買った場合と5個入り買った場合で安い方をdpテーブルに記録する)
- dp_a = i > 2 ? dp[i - 2] + a : a
dp[n..]にn個~n+4個購入時の最安値が記録されているので最小値を返す。
入出力例1の処理

dpテーブルを初期化した状態。
0個買うときの最安値は0
ここからi = 1~8 (4+4)のループ
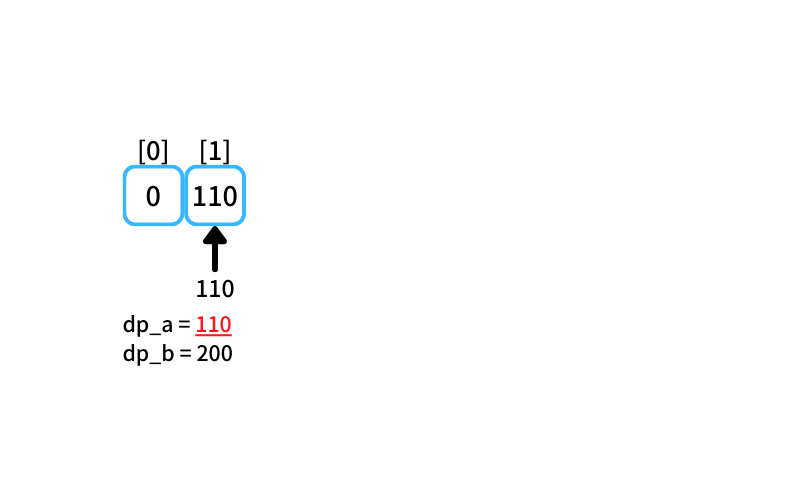
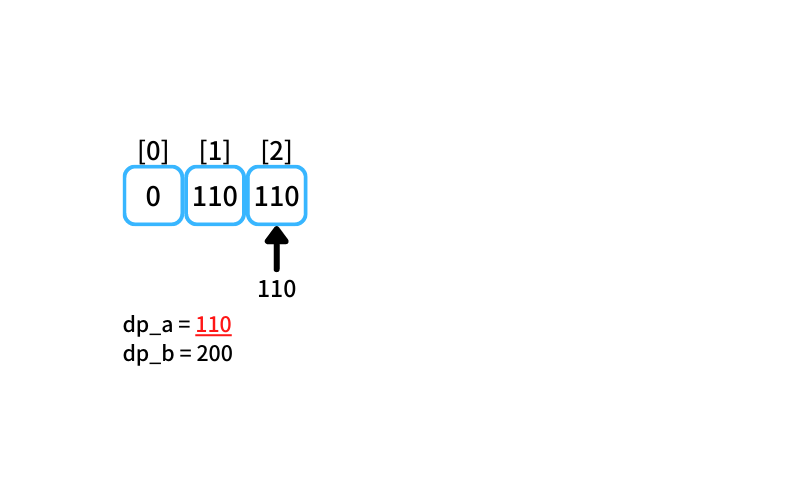
i = 1~2 : 1~2個買うときの最安値
- 2個入りを買う場合
db_a = 110 - 5個入りを買う場合
db_b = 200
1~2個買うときの最安値は110円(2個入りを1つ買う)
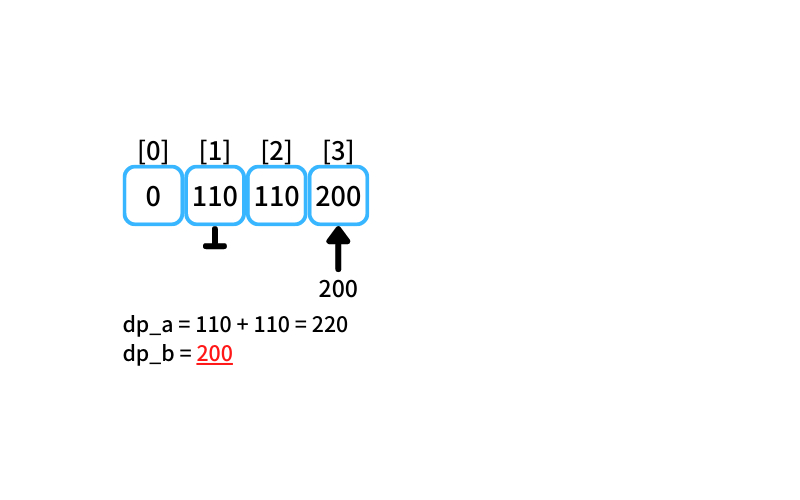
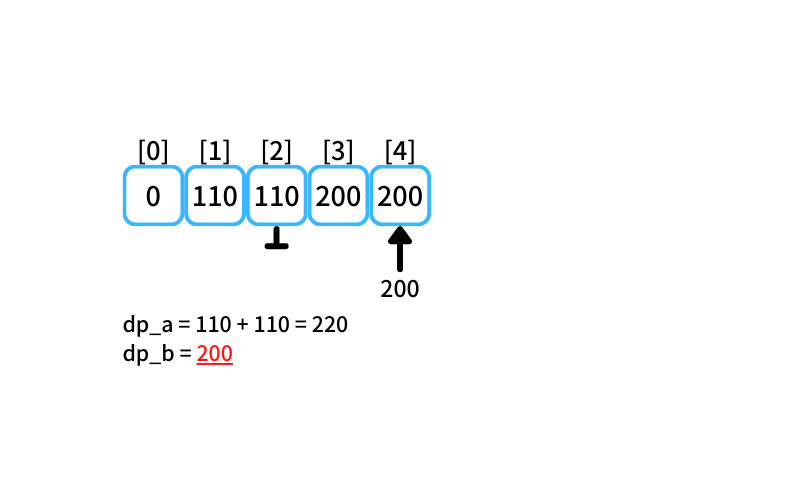
i = 3~4 : 3~4個買うときの最安値
- 2個入りを買う場合
db_a = 110 + 110 = 220 - 5個入りを買う場合
db_b = 200
3~4個買うときの最安値は200円(5個入りのりんごを1つ買う)
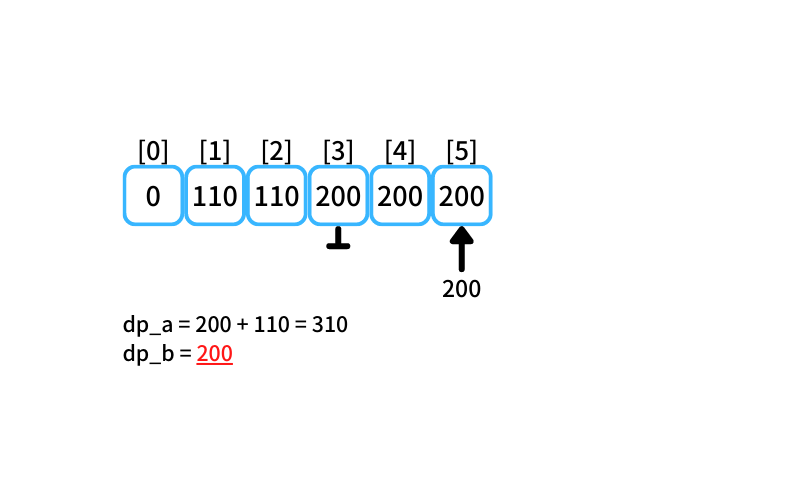
i = 5 : 5個買うときの最安値
- 2個入りを買う場合
db_a = 200 + 110 = 310 - 5個入りを買う場合
db_b = 200
5個買うときの最安値は200円(5個入りのりんごを1つ買う)
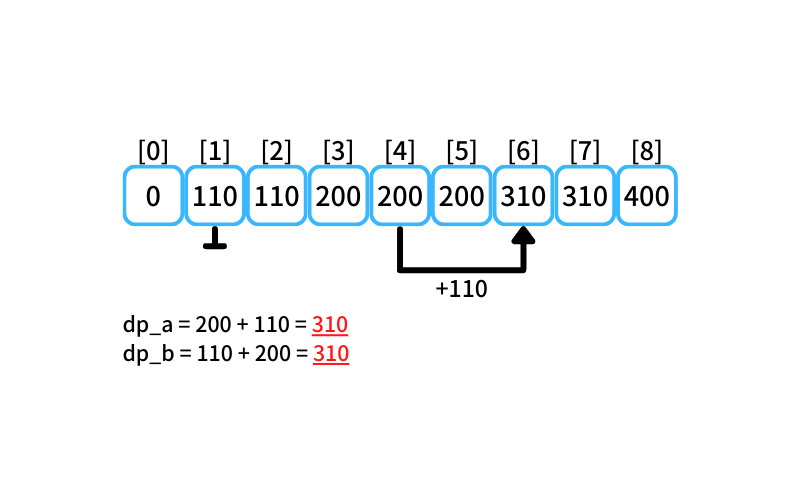
i = 6 : 6個買うときの最安値
- 2個入りを買う場合
db_a = 200 + 110 = 310 - 5個入りを買う場合
db_b = 110 + 200 = 310
6個買うときの最安値は310円(2個入りを1つと5個入りを1つ買う)
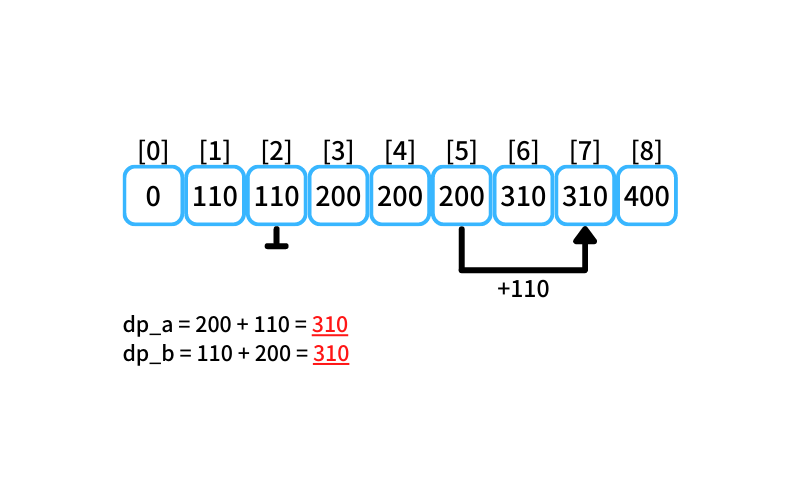
i = 7 : 7個買うときの最安値
- 2個入りを買う場合
db_a = 200 + 110 = 310 - 5個入りを買う場合
db_b = 110 + 200 = 310
7個買うときの最安値は310円(2個入りを1つと5個入りを1つ買う)
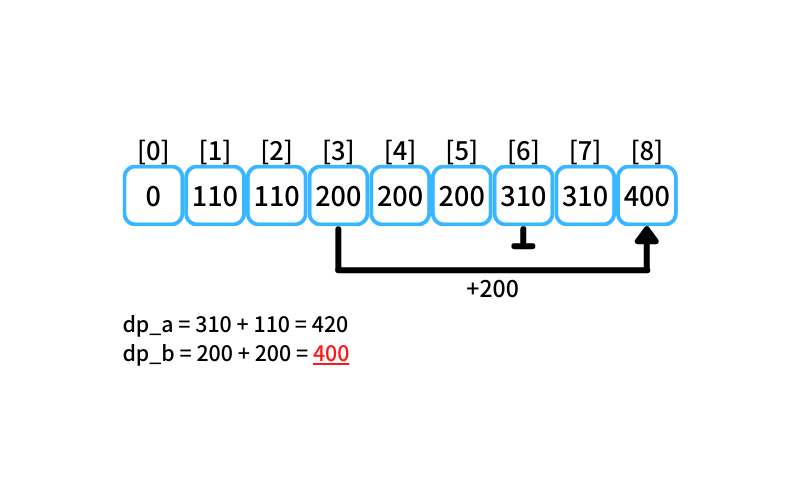
i = 8 : 8個買うときの最安値
- 2個入りを買う場合
db_a = 310 + 110 = 420 - 5個入りを買う場合
db_b = 200 + 200 = 400
8個買うときの最安値は400円(5個入りを2つ買う)
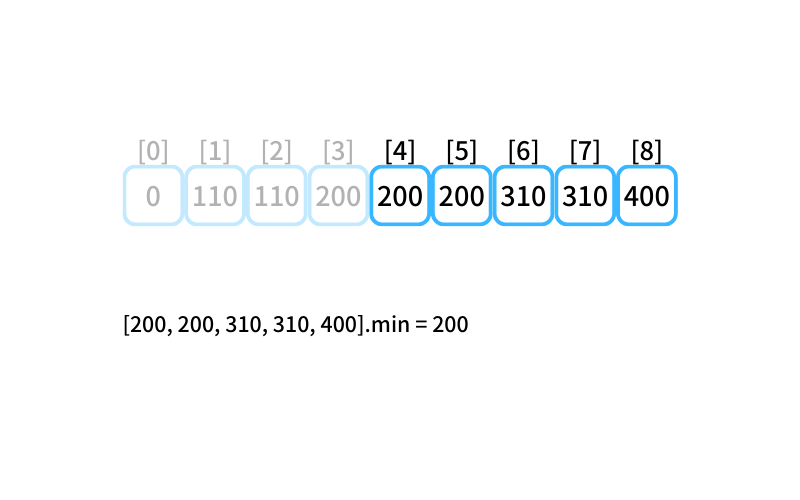
dp[4]~dp[8]の中で最小は 200 なので、
4個買うときの最安値は200円(5個入りを1つ買う)
STEP3: 最安値を達成するには 3 (paizaランク B 相当)
りんごx個が a 円で、りんごy個が b 円のとき、n 個のりんごを手に入れるための最安値を求める問題です。
(最安値ならりんごがn個以上になっても良い)
漸化式
- dp
- dp[i] = 0 (i = 0)
- dp[i] = [dp_a[i], dp_b[i]].min (0 < i)
(x個とy個購入した最安値のうち安い方を記録)
- dp_a (x個購入した場合の最安値)
- dp_a[i] = a (i ≦ x)
- dp_a[i] = dp[i - x] + a (x < i)
- dp_b (y個購入した場合の最安値)
- dp_b[i] = b (i ≦ y)
- dp_b[i] = dp[i - y] + a (y < i)
解答例
INPUT1 = <<~"EOS"
4 2 110 5 200
EOS
OUTPUT1 = <<~"EOS"
200
EOS
def solve(input_lines)
n, x, a, y, b = input_lines.split.map(&:to_i)
# dpテーブル初期化
# 0 個購入: 0 円
dp = [0]
# dpテーブル更新
1.upto(n + [x, y].max) do |i|
dp_a = i > x ? dp[i - x] + a : a
dp_b = i > y ? dp[i - y] + b : b
# x 個買った場合と y 個買った場合で安い方を記録する
dp << [dp_a, dp_b].min
end
# n 個以上購入時の最安値を返す
dp[n..].min
end
puts solve(STDIN.read)
# 確認用コード
# p solve(INPUT1)
# > 200
※ 2個がx, 5個がyに置き換わるだけで、STEP2と同じ問題です。
整数n, x, a, y, bを受け取る。dpに[0]を代入する。(0個の最安値は0円)i = 1 ~ n + [a, b].maxで繰り返し処理を設定する。
(n個丁度買うときより多く買った方が安い場合があるので多めに(n+[a, b].max個まで)調べる)- dp_a = i > x ? dp[i - x] + a : a
(x個入りを買ってi個(以上)にした場合の価格をdp_aとする) - dp_b = i > y ? dp[i - y] + b : b
(y個入りを買ってi個(以上)にした場合の価格をdp_bとする) - dp << [dp_a, dp_b].min
(x個入りを買った場合とy個入り買った場合で安い方をdpテーブルに記録する)
- dp_a = i > x ? dp[i - x] + a : a
dp[n..]にn個~n+[a, b].max個購入時の最安値が記録されているので最小値を返す。
FINAL問題: 最安値を達成するには 4 (paizaランク B 相当)
※ paizaレベルアップ問題集 DPメニューより
問題
八百屋にて、りんご x 個が a 円で、りんご y 個が b 円で、りんご z 個が c 円で売られています。
りんごの買い方を工夫したとき、n 個のりんごを手に入れるために必要な金額の最小値はいくらでしょうか。なお、買い方を工夫した結果、買ったりんごが n+1 個以上になってもよいものとします。
入力される値
n x a y b z c
入力値最終行の末尾に改行が1つ入ります。
期待する出力
りんごを n 個手に入れるために必要な金額の最小値を出力してください。
また、末尾に改行を入れ、余計な文字、空行を含んではいけません。
条件
すべてのテストケースにおいて、以下の条件をみたします。
- 1 ≦ n ≦ 1,000
- 1 ≦ x ≦ 1,000
- 1 ≦ y ≦ 1,000
- 1 ≦ z ≦ 1,000
- x < y < z
- 1 ≦ a ≦ 10,000
- 1 ≦ b ≦ 10,000
- 1 ≦ c ≦ 10,000
- a < b < c
- 入力例1
- 9 2 100 3 125 5 200
- 出力例1
- 375
攻略ポイント
ポイント
- 漸化式を立てて問題を解く。
問題を解く流れ
入出力例をコピペしてヒアドキュメントで変数に代入し、データを確認します。正しく受け取れていれば確認用コードは削除します。
INPUT1 = <<~"EOS" 9 2 100 3 125 5 200 EOS OUTPUT1 = <<~"EOS" 375 EOS # 確認用コード p INPUT1 # > "9 2 100 3 125 5 200\n" p OUTPUT1 # > "375\n"
続いて、問題を解くsolveメソッドを変数の下に定義し、入力データを受け取る処理を書きます。
def solve(input_lines) n, x, a, y, b, z, c = input_lines.split.map(&:to_i) # 確認用コード [n, x, a, y, b, z, c] end # 確認用コード p solve(INPUT1) # > [9, 2, 100, 3, 125, 5, 200]
データが正しく受け取れていれば、solve メソッドに処理を追加していきます。
※ x, y, z の3種類に増えますがSTEP2と同じ問題です。
整数n, x, a, y, b, z, cを受け取る。dpに[0]を代入する。(0個の最安値は0円)i = 1 ~ n + [a, b, c].maxで繰り返し処理を設定する。
(n個丁度買うときより多く買った方が安い場合があるので多めに(n+[a, b, c].max個まで)調べる)- dp_a = i > x ? dp[i - x] + a : a
(x個入りを買ってi個(以上)にした場合の価格をdp_aとする) - dp_b = i > y ? dp[i - y] + b : b
(y個入りを買ってi個(以上)にした場合の価格をdp_bとする) - dp_c = i > z ? dp[i - z] + c : c
(z個入りを買ってi個(以上)にした場合の価格をdp_cとする) - dp << [dp_a, dp_b, dp_c].min
(2個入りを買った場合と5個入り買った場合で安い方をdpテーブルに記録する)
- dp_a = i > x ? dp[i - x] + a : a
def solve(input_lines)
n, x, a, y, b, z, c = input_lines.split.map(&:to_i)
# dpテーブル初期化
# 0 個購入: 0 円
dp = [0]
# dpテーブル更新
1.upto(n + [x, y, z].max) do |i|
dp_a = i > x ? dp[i - x] + a : a
dp_b = i > y ? dp[i - y] + b : b
dp_c = i > z ? dp[i - z] + c : c
# x 個, y 個, z個 買った場合の最安値を記録する
dp << [dp_a, dp_b, dp_c].min
end
# 確認用コード
dp
end
# 確認用コード
p solve(INPUT1)
# > [0, 100, 100, 125, 200, 200, 250, 300, 325, 375, 400, 450, 500, 525, 575]
p solve(INPUT1) == OUTPUT1
# > false
あとは出力形式を整えれば完成です。
p solve(INPUT1) == OUTPUT1 -> true を確認するために、出力を文字列に変換して末尾に改行を加えます。
def solve(input_lines)
n, x, a, y, b, z, c = input_lines.split.map(&:to_i)
# dpテーブル初期化
# 0 個購入: 0 円
dp = [0]
# dpテーブル更新
1.upto(n + [x, y, z].max) do |i|
dp_a = i > x ? dp[i - x] + a : a
dp_b = i > y ? dp[i - y] + b : b
dp_c = i > z ? dp[i - z] + c : c
# x 個, y 個, z個 買った場合の最安値を記録する
dp << [dp_a, dp_b, dp_c].min
end
# n個以上購入時の最安値を返す
dp[n..].min.to_s << "\n"
end
# 確認用コード
p solve(INPUT1)
# > [0, 100, 100, 125, 200, 200, 250, 300, 325, 375, 400, 450, 500, 525, 575]
p solve(INPUT1) == OUTPUT1
# > false
入出力例での動作確認が出来ましたので、標準入力からのデータ受け取りに変更して、手動で動作確認をしたら提出します。
複数行のデータ受け取りなので STDIN.read を使います。(入力終了は Ctrl+D 又は Ctrl+Z)
解答コード
def solve(input_lines)
n, x, a, y, b, z, c = input_lines.split.map(&:to_i)
# dpテーブル初期化
# 0 個購入: 0 円
dp = [0]
# dpテーブル更新
1.upto(n + [x, y, z].max) do |i|
dp_a = i > x ? dp[i - x] + a : a
dp_b = i > y ? dp[i - y] + b : b
dp_c = i > z ? dp[i - z] + c : c
# x 個, y 個, z個 買った場合の最安値を記録する
dp << [dp_a, dp_b, dp_c].min
end
# n個以上購入時の最安値を返す
dp[n..].min.to_s << "\n"
end
p solve(STDIN.read)
入出力例1の処理

dpテーブルを初期化した状態。
0個買うときの最安値は0
ここからi = 1 ~ 14 (9 + 5)のループ

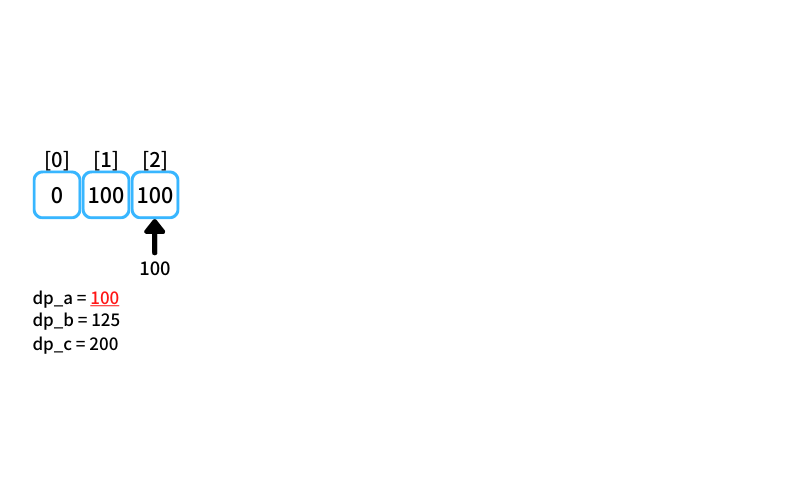
i = 1~2 : 1~2個買うときの最安値
- 2個入りを買う場合
db_a = 100 - 3個入りを買う場合
db_b = 125 - 5個入りを買う場合
db_c = 200
1~2個買うときの最安値は100円(2個入りを1つ買う)
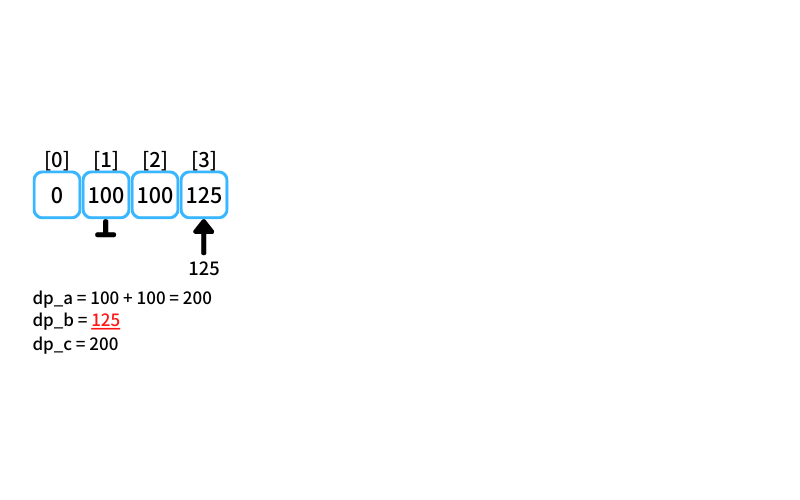
i = 3 : 3個買うときの最安値
- 2個入りを買う場合
db_a = 100 + 100 = 200 - 3個入りを買う場合
db_b = 125 - 5個入りを買う場合
db_c = 200
3個買うときの最安値は125円(3個入りを1つ買う)
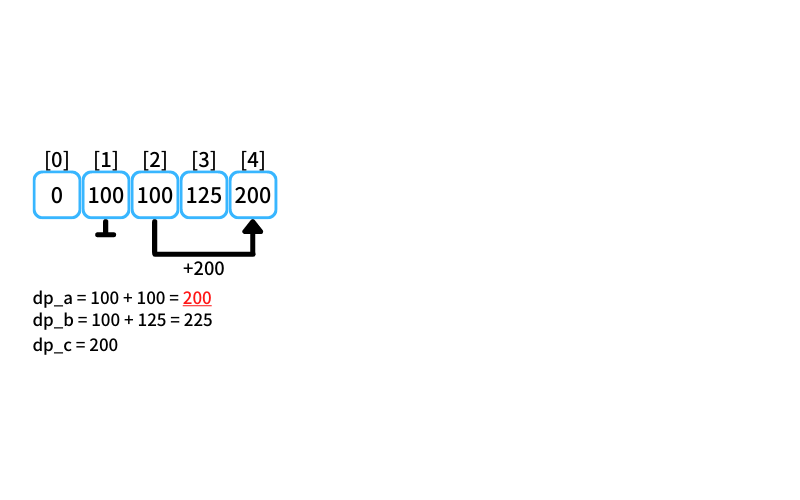
i = 4 : 4個買うときの最安値
- 2個入りを買う場合
db_a = 100 + 100 = 200 - 3個入りを買う場合
db_b = 125 - 5個入りを買う場合
db_c = 200
4個買うときの最安値は200円(2個入りを2つ買う)
※ 5個入りを買った方がお得ですが、今回の実装では2個入り2つが採用されます。
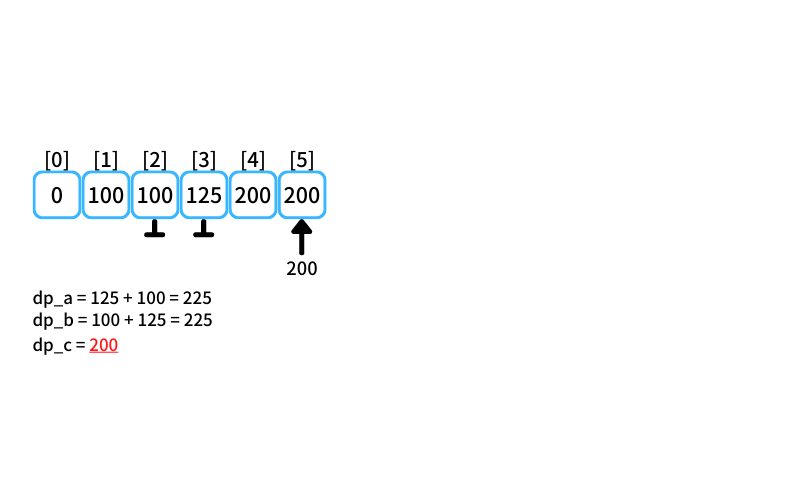
i = 5 : 5個買うときの最安値
- 2個入りを買う場合
db_a = 125 + 100 = 225 - 3個入りを買う場合
db_b = 100 + 125 = 225 - 5個入りを買う場合
db_c = 200
5個買うときの最安値は200円(5個入りを1つ買う)
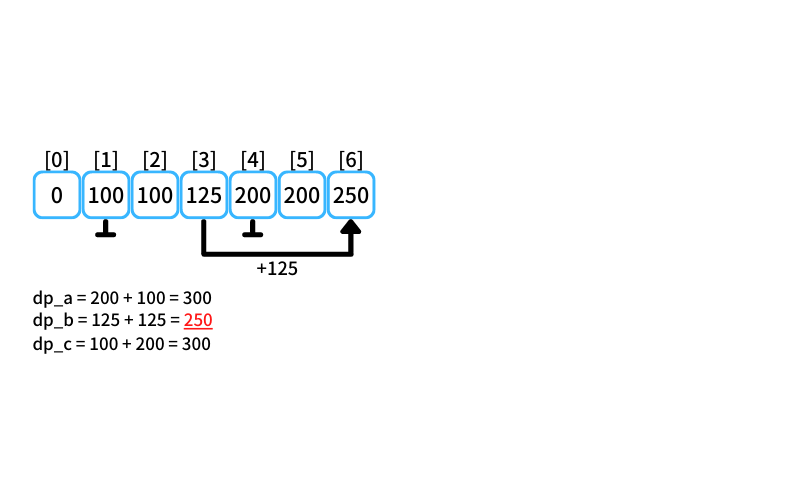
i = 6 : 6個買うときの最安値
- 2個入りを買う場合
db_a = 200 + 100 = 300 - 3個入りを買う場合
db_b = 125 + 125 = 250 - 5個入りを買う場合
db_c = 100 + 200 = 300
6個買うときの最安値は250円(3個入りを2つ買う)
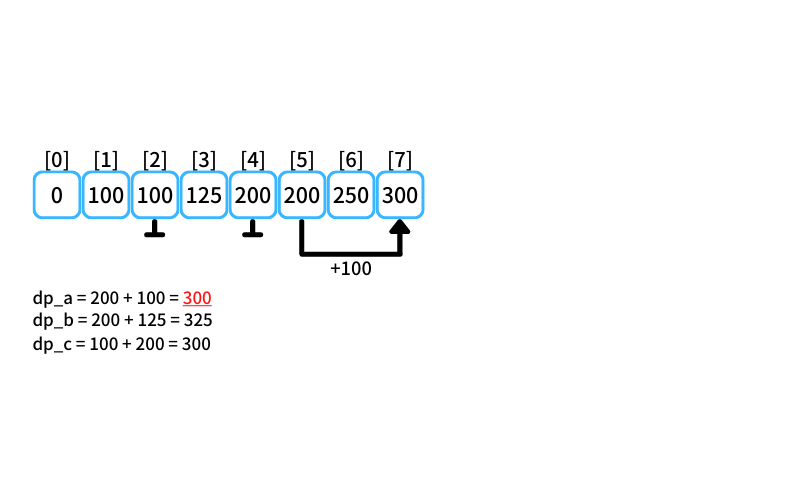
i = 7 : 7個買うときの最安値
- 2個入りを買う場合
db_a = 200 + 100 = 300 - 3個入りを買う場合
db_b = 200 + 125 = 325 - 5個入りを買う場合
db_c = 100 + 200 = 300
7個買うときの最安値は300円(2個入りを1つと5個入りを1つ買う)
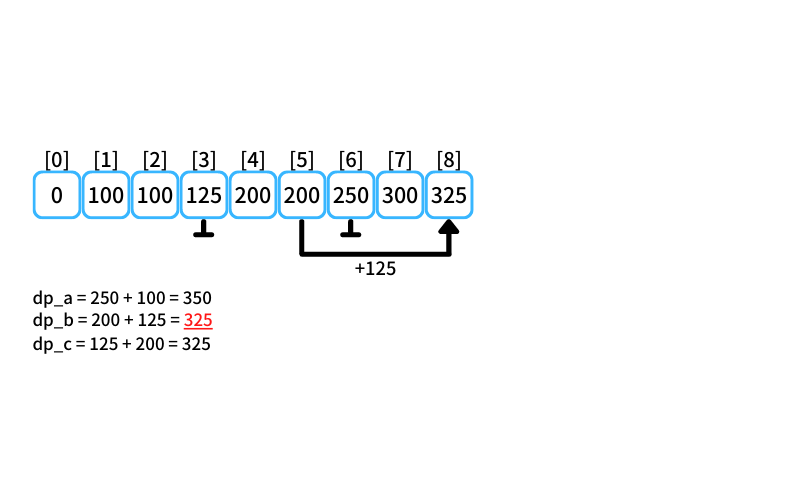
i = 8 : 8個買うときの最安値
- 2個入りを買う場合
db_a = 250 + 100 = 350 - 3個入りを買う場合
db_b = 200 + 125 = 325 - 5個入りを買う場合
db_c = 125 + 200 = 325
8個買うときの最安値は325円(3個入りを1つと5個入りを1つ買う)
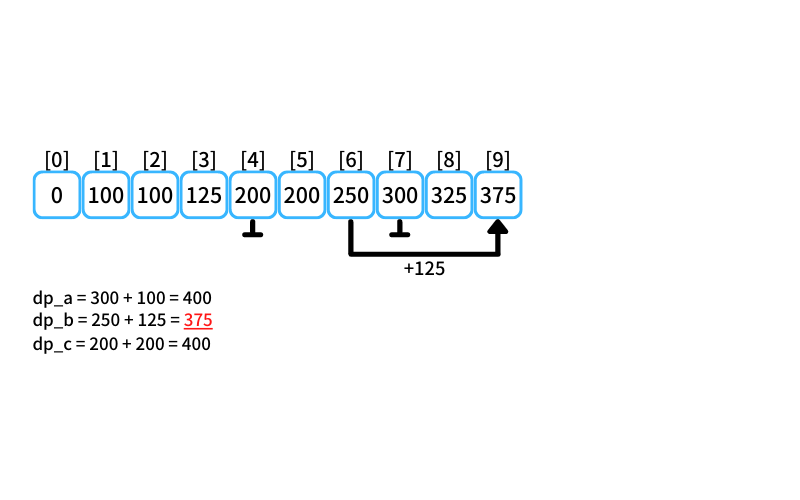
i = 9 : 9個買うときの最安値
- 2個入りを買う場合
db_a = 300 + 100 = 400 - 3個入りを買う場合
db_b = 250 + 125 = 375 - 5個入りを買う場合
db_c = 200 + 200 = 400
9個買うときの最安値は375円(3個入りを3つ買う)
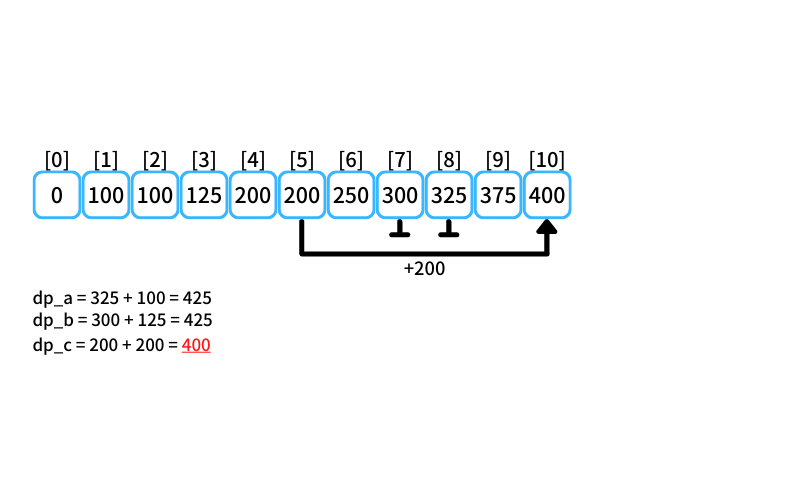
i = 10 : 10個買うときの最安値
- 2個入りを買う場合
db_a = 325 + 100 = 425 - 3個入りを買う場合
db_b = 300 + 125 = 425 - 5個入りを買う場合
db_c = 200 + 200 = 400
10個買うときの最安値は400円(5個入りを2つ買う)
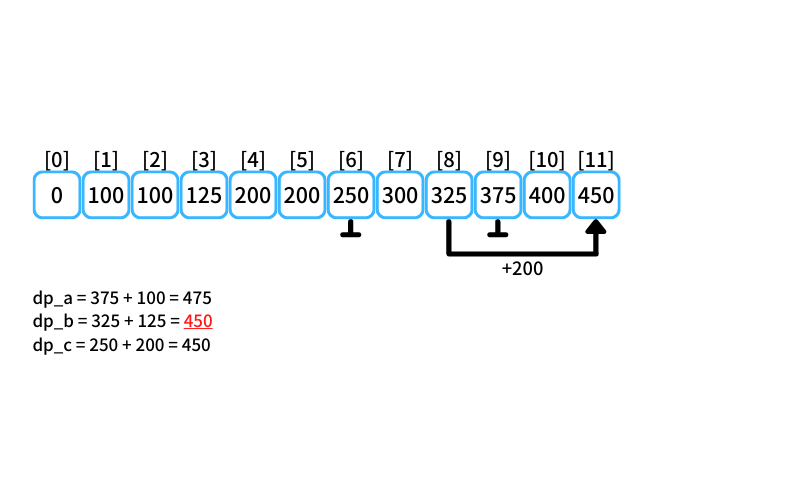
i = 11 : 11個買うときの最安値
- 2個入りを買う場合
db_a = 375 + 100 = 475 - 3個入りを買う場合
db_b = 325 + 125 = 450 - 5個入りを買う場合
db_c = 250 + 200 = 450
11個買うときの最安値は400円(3個入りを2つと5個入りを1つ買う)
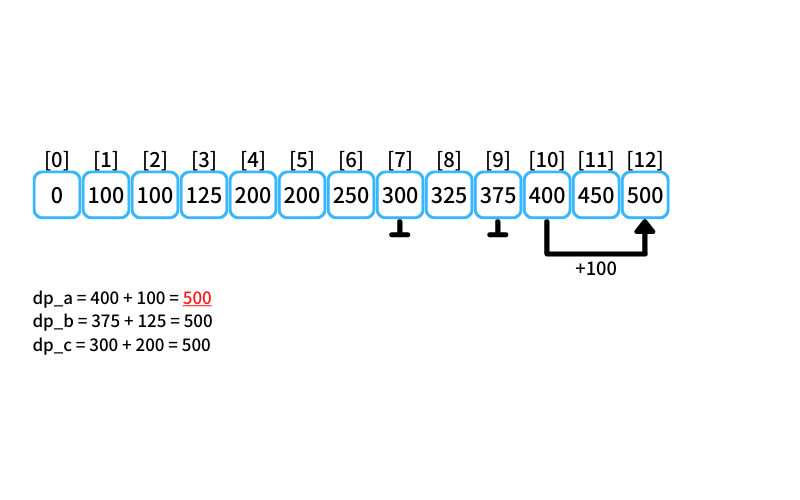
i = 12 : 12個買うときの最安値
- 2個入りを買う場合
db_a = 400 + 100 = 500 - 3個入りを買う場合
db_b = 375 + 125 = 500 - 5個入りを買う場合
db_c = 300 + 200 = 500
12個買うときの最安値は500円(2個入りを1つと5個入りを2つ買う)
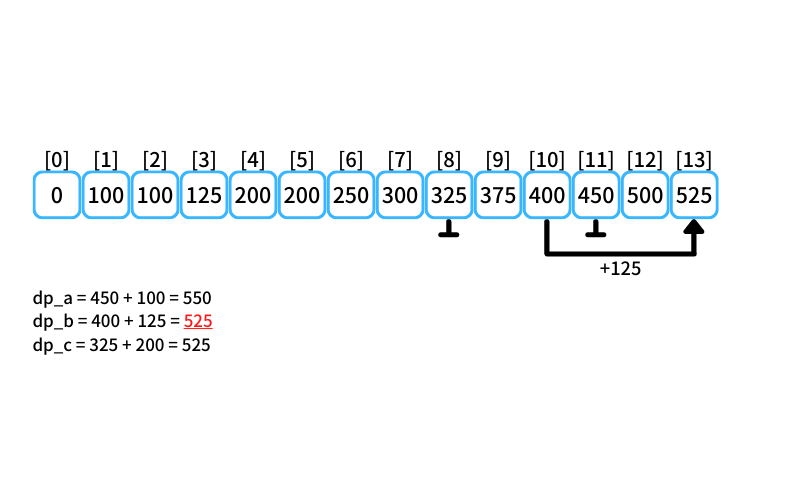
i = 13 : 13個買うときの最安値
- 2個入りを買う場合
db_a = 450 + 100 = 550 - 3個入りを買う場合
db_b = 400 + 125 = 525 - 5個入りを買う場合
db_c = 325 + 200 = 525
13個買うときの最安値は525円(3個入りを1つと5個入りを2つ買う)
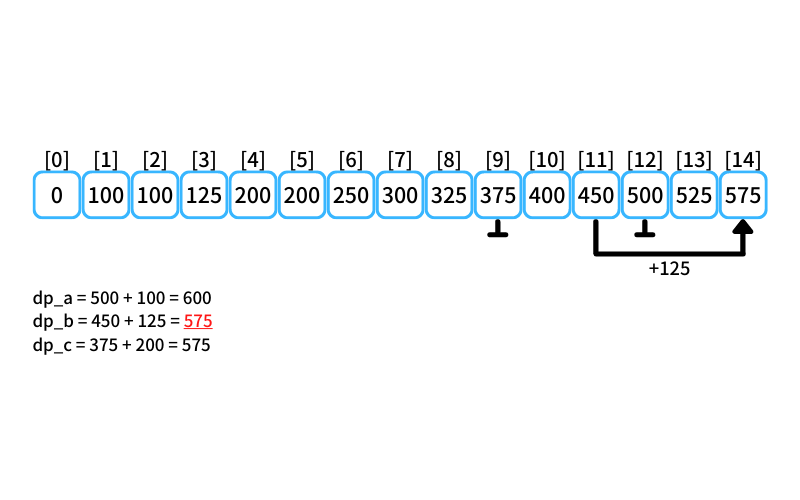
i = 14 : 14個買うときの最安値
- 2個入りを買う場合
db_a = 500 + 100 = 600 - 3個入りを買う場合
db_b = 450 + 125 = 575 - 5個入りを買う場合
db_c = 375 + 200 = 575
14個買うときの最安値は500円(3個入りを3つと5個入りを1つ買う)
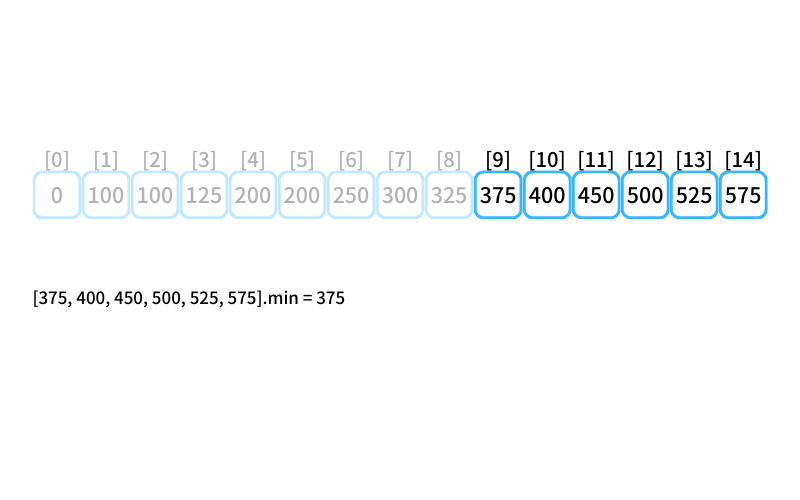
dp[9]~dp[14]の中で最小は 375 なので、
9個買うときの最安値は375円(3個入りを3つ買う)
今回のまとめ
セクション3は複数の漸化式をたてて、その中から最小値を選択して問題を解く課題でした。

以前も同じコメントをしましたが、dpテーブルの図を自分でも書いてみると理解が深まりますよ!




