こんにちは!じゃいごテックのあつしです。
今回はpaiza DPメニュー 「セクション5【部分列】 STEP1, FINAL」 を解説します。
DPメニューは動的計画法(Dynamic Programming, DP)に関する6個のセクションで構成されています。
セクション5【部分列】は、配列からいくつかの要素を取り出して、隣り合う数列の値が常に大きい(または常に小さい)区間のうち、最長であるものの長さを求める問題です。
※ 部分列:飛び飛びはOKですが、要素の順番を変えてはいけません。
STEP問題 を解いてみる
簡単な解説は付けていますが、難しいと感じたら下記の記事も参考にしてみて下さい。
分割統治法・動的計画法
メソッドの定義と呼び出し
標準入力・標準出力
STEP1: 最長部分増加列 (paizaランク B 相当)
n本分の木の長さの配列aが与えられるので、最長の増加部分列の長さを求める問題です。
解答例
INPUT1 = <<~"EOS"
5
100
102
101
91
199
EOS
OUTPUT1 = <<~"EOS"
3
EOS
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# dpテーブル初期化
dp = [1] * n
# dpテーブル更新
1.upto(n - 1) do |i|
0.upto(i - 1) do |j|
if a[j] < a[i]
# 最後が木 j であるような増加部分列の末尾に木 i をくっつける
dp[i] = [dp[i], dp[j] + 1].max
end
end
end
# 最大値を返す
dp.max
end
puts solve(STDIN.read)
# 確認用コード
# puts solve(INPUT1)
# > 3
整数n, 配列aを受け取る。dpに[1] * nを代入する。
(要素単体での最長は1)i = 1 ~ n-1で繰り返し処理を設定する。j = 0 ~ i-1で繰り返し処理を設定する。- a[j] > a[i] なら dp[i] を [dp[i], dp[j] + 1].max で更新する
- dpの最大値(増加部分列が最大になる区間の長さ)を返す
入出力例1の処理
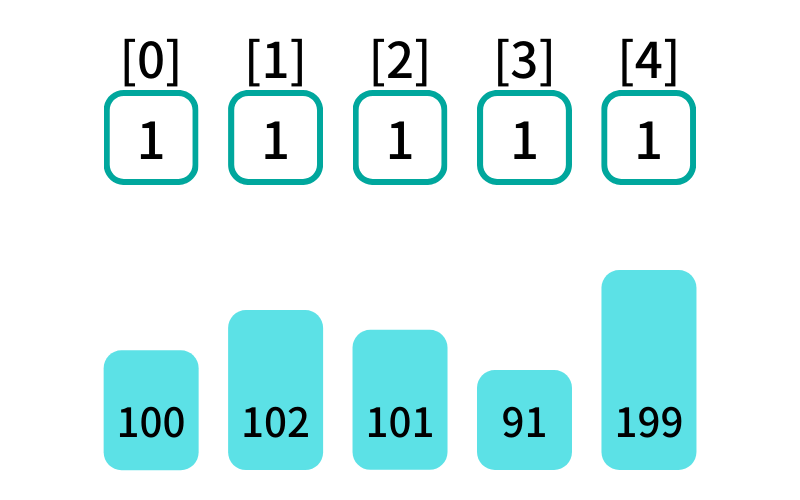
dp = [1] * 5 で初期化
単体での増加部分列は1
ここからi = 1 ~ n-1のループ
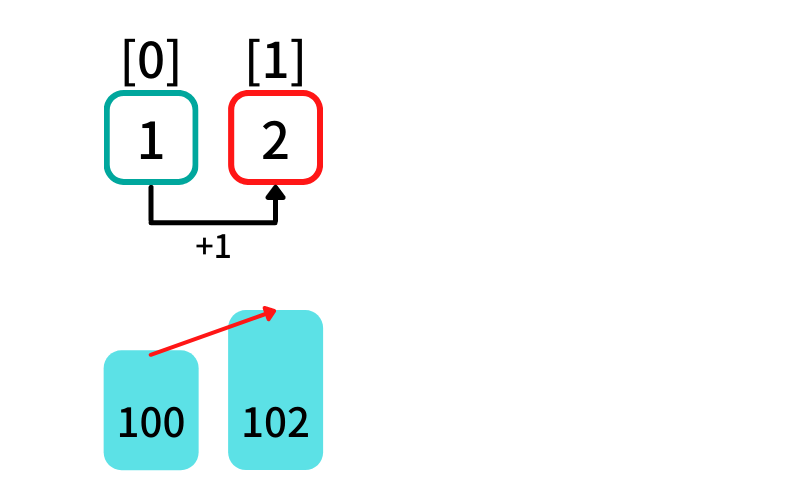
木[1]より手前の項について調べる (i = 1, j = 0)
- 木[0]: dp[0] = 1 , 木[0](100) < 木[1](102) -> True
木[j] < 木[1] を満たし、最初に出現する最大増加部分列に 木[1] を追加する
dp[1] = dp[0](1) + 1 = 2
木[1]が末尾の増加部分列の長さは[0, 1]を選んだ時の2
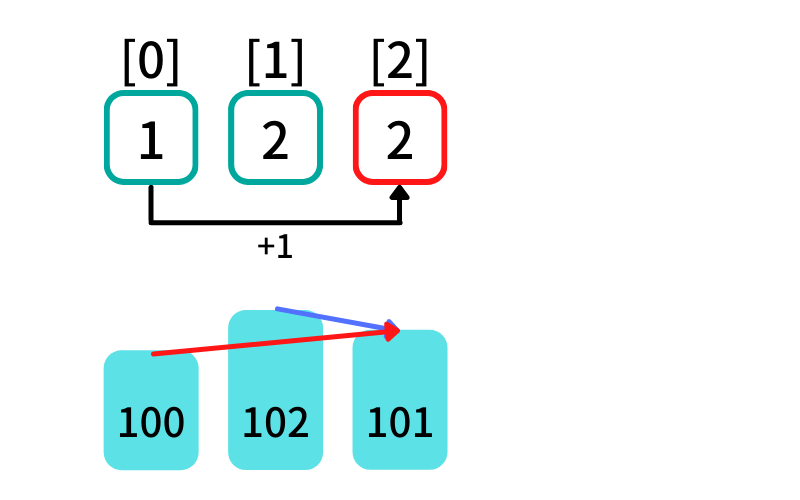
木[2]より手前の項について調べる (i = 2, j = 0, 1)
- 木[0]: dp[0] = 1 , 木[0](100) < 木[2](101) -> True
- 木[1]: dp[1] = 1 , 木[1](102) < 木[2](101) -> False
木[j] < 木[2] を満たし、最初に出現する最大増加部分列に 木[2] を追加する
dp[2] = dp[0](1) + 1 = 2
木[2]が末尾の増加部分列の長さは[0, 2]を選んだ時の2
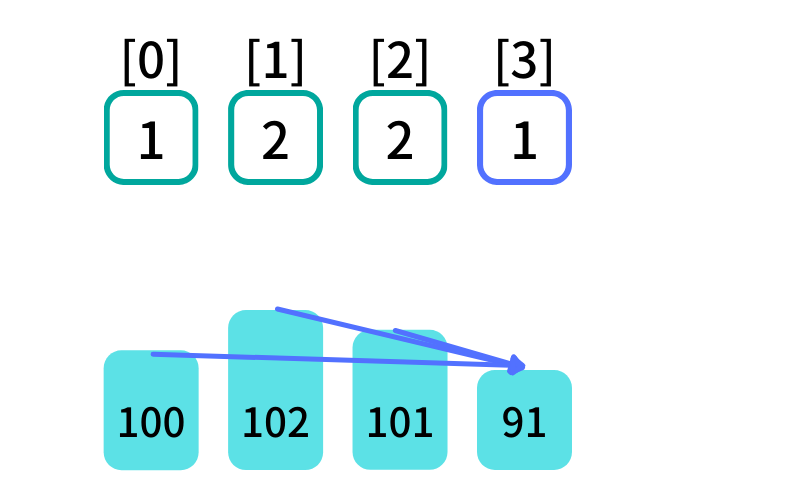
木[3]より手前の項について調べる (i = 3, j = 0, 1, 2)
- 木[0]: dp[0] = 1 , 木[0](100) < 木[3](91) -> False
- 木[1]: dp[1] = 2 , 木[1](102) < 木[3](91) -> False
- 木[2]: dp[2] = 2 , 木[2](101) < 木[3](91) -> False
木[j] < 木[3] を満たし、最初に出現する最大増加部分列に 木[3] を追加する
条件を満たすものがないのでdp[3]の更新なし
木[3]が末尾の増加部分列の長さは[3]を選んだ時の1
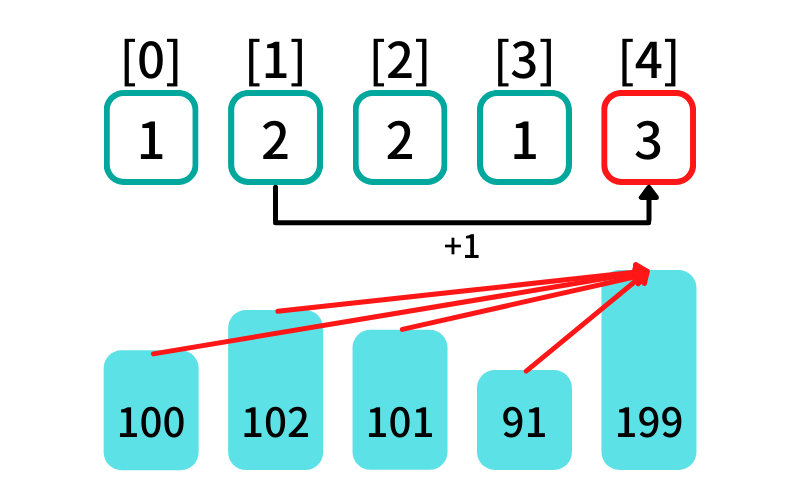
木[4]より手前の項について調べる (i = 4, j = 0, 1, 2, 3)
- 木[0]: dp[0] = 1 , 木[0](100) < 木[4](199) -> True
- 木[1]: dp[1] = 2 , 木[1](102) < 木[4](199) -> True
- 木[2]: dp[2] = 2 , 木[2](101) < 木[4](199) -> True
- 木[3]: dp[3] = 1 , 木[3](101) < 木[4](199) -> True
木[j] < 木[4] を満たし、最初に出現する最大増加部分列に 木[4] を追加する
dp[4] = dp[1](2) + 1 = 3
木[4]が末尾の増加部分列の長さは[0, 1, 4]を選んだ時の3
- 配列aで増加部分列が最大になる要素の組み合わせは [0, 1, 4](100, 102, 199)
- 配列aで増加部分列が最大になる区間の長さは3
FINAL問題: 最長減少部分列 (paizaランク B 相当)
※ paizaレベルアップ問題集 DPメニューより
問題
n 本の木が横一列に並んでいます。左から i 番目の木を木 i と呼ぶことにします。木 i の高さは a_i [cm] です。
あなたは、何本かの木を伐採することによって、残った木を左から順に見ると高さが単調減少になっているようにしたいと考えています。つまり、残った木を左から 木 k_1, 木 k_2, ... , 木 k_m とすると、a_{k_1} > a_{k_2} > ... > a_{k_m} が満たされているようにしたいです。なるべく多くの木が残るように工夫して伐採する木を選んだとき、伐採されずに残る木の本数が最大でいくつになるか求めてください。
なお、最初から n 本の木が単調減少に並んでいる場合は、1本も伐採しなくてよいものとします。
入力される値
n
a_1
a_2
...
a_n
- 1行目に、横一列に並んでいる木の本数 n が与えられます。
- 続く n 行のうち i 行目では、木 i の高さ a_i が与えられます。
入力値最終行の末尾に改行が1つ入ります。
期待する出力
残った木を左から見ると高さが単調減少になっているように木を伐採したとき、伐採されずに残る木の本数の最大値を出力してください。
また、末尾に改行を入れ、余計な文字、空行を含んではいけません。
条件
すべてのテストケースにおいて、以下の条件をみたします。
- 1 ≦ n ≦ 5,000
- 1 ≦ a_i ≦ 1,000,000,000
- a_i ≠ a_j (i ≠ j)
- 入力例1
- 5
109
110
108
103
100
- 出力例1
- 4
攻略ポイント
ポイント
- 前の項より値が低いものを選択して最大の長さの列を作る。
問題を解く流れ
入出力例をコピペしてヒアドキュメントで変数に代入し、データを確認します。正しく受け取れていれば確認用コードは削除します。
INPUT1 = <<~"EOS" 5 109 110 108 103 100 EOS OUTPUT1 = <<~"EOS" 4 EOS # 確認用コード p INPUT1 # > "5\n109\n110\n108\n103\n100\n" p OUTPUT1 # > "4\n"
続いて、問題を解くsolveメソッドを変数の下に定義し、入力データを受け取る処理を書きます。
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# 確認用コード
[n, a]
end
# 確認用コード
p solve(INPUT1)
# > [5, [109, 110, 108, 103, 100]]
データが正しく受け取れていれば、solve メソッドに処理を追加していきます。
※ 不等号の向きが変わるだけで、STEP1と同じ問題です。
-
整数n, 配列aを受け取る。dpに[1] * nを代入する。
(要素単体での部分列は1)i = 1 ~ n-1で繰り返し処理を設定する。-
j = 1 ~ i-1で繰り返し処理を設定する。- もし
a[j] > a[i]かつdp[i] < dp[j] + 1ならdp[i] を dp[j] + 1で更新する
- もし
-
- dpの最大値(減少部分列が最大になる区間の長さ)を返す
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# dpテーブル初期化
dp = [1] * n
# dpテーブル更新
1.upto(n - 1).each do |i|
0.upto(i - 1).each do |j|
if a[j] > a[i]
# 最後が木 j であるような減少部分列の末尾に木 i をくっつける
dp[i] = [dp[i], dp[j] + 1].max
end
end
end
# 確認用コード
dp
end
# 確認用コード
p solve(INPUT1)
# > [1, 1, 2, 3, 4]
p solve(INPUT1) == OUTPUT1
# > false
dpテーブルの内容が良さそうなら、出力を整えれば完成です。
p solve(INPUT1) == OUTPUT1 -> true を確認するために、出力を文字列に変換して末尾に改行を加えます。
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# dpテーブル初期化
dp = [1] * n
# dpテーブル更新
1.upto(n - 1).each do |i|
0.upto(i - 1).each do |j|
if a[j] > a[i]
# 最後が木 j であるような減少部分列の末尾に木 i をくっつける
dp[i] = [dp[i], dp[j] + 1].max
end
end
end
# 減少部分列が最大になる区間の長さを文字列に変換し末尾に改行を追加
dp.max.to_s << "\n"
end
# 確認用コード
p solve(INPUT1)
# > "4\n"
p solve(INPUT1) == OUTPUT1
# > true
入出力例での動作確認が出来ましたので、標準入力からのデータ受け取りに変更して、手動で動作確認をしたら提出します。
複数行のデータ受け取りなので STDIN.read を使います。(入力終了は Ctrl+D 又は Ctrl+Z)
解答コード
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# dpテーブル初期化
dp = [1] * n
# dpテーブル更新
1.upto(n - 1).each do |i|
0.upto(i - 1).each do |j|
if a[j] > a[i]
# 最後が木 j であるような減少部分列の末尾に木 i をくっつける
dp[i] = [dp[i], dp[j] + 1].max
end
end
end
# 減少部分列が最大になる区間の長さを文字列に変換し末尾に改行を追加
dp.max.to_s << "\n"
end
puts solve(STDIN.read)
入出力例1の処理
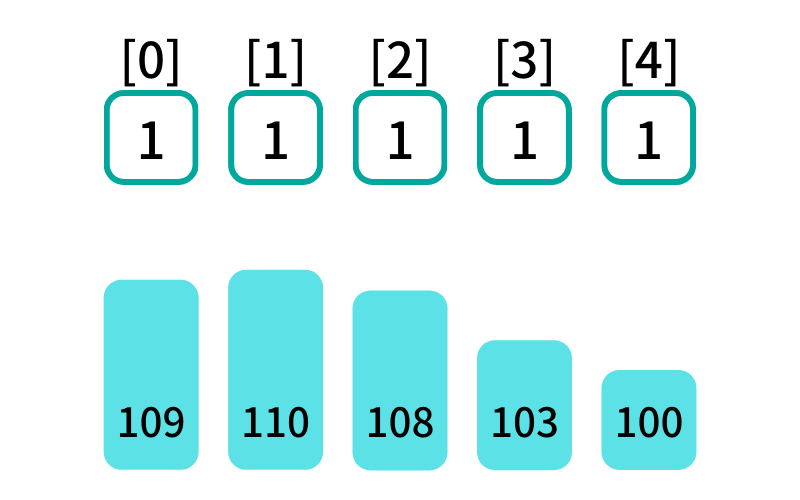
dp = [1] * 5 で初期化
単体での減少部分列は1
ここからi = 1 ~ n-1のループ
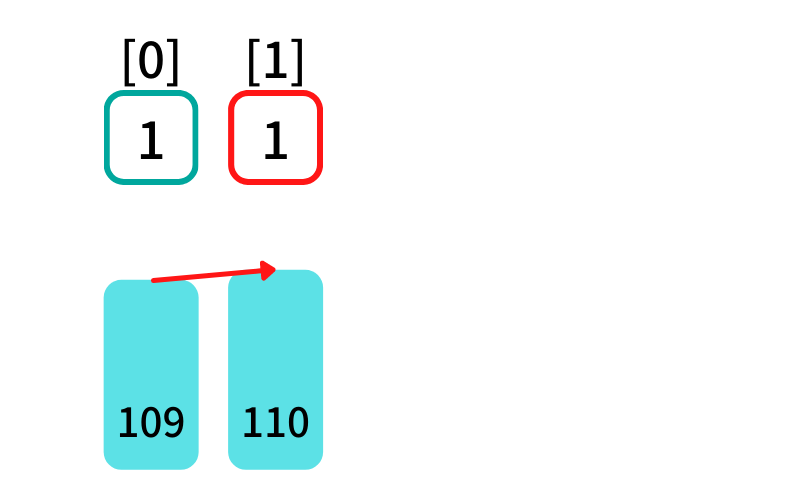
木[1]より手前の項について調べる (i = 1, j = 0)
- 木[0]: dp[0] = 1 , 木[0](109) > 木[1](110) -> False
木[j] > 木[1] を満たし、最初に出現する最大減少部分列に 木[1] を追加する
条件を満たすものがないのでdp[1]の更新なし
木[1]が末尾の減少部分列の長さは[1]を選んだ時の1
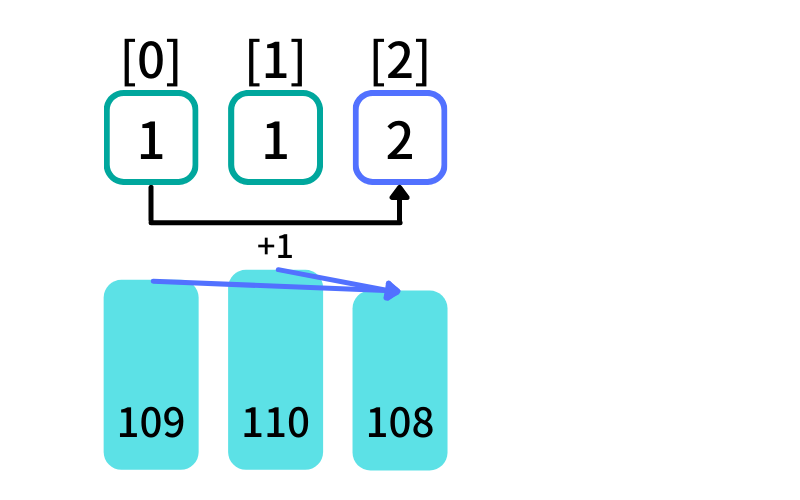
木[2]より手前の項について調べる (i = 2, j = 0, 1)
- 木[0]: dp[0] = 1 , 木[0](109) > 木[2](108) -> True
- 木[1]: dp[1] = 1 , 木[1](110) > 木[2](108) -> False
木[j] > 木[2] を満たし、最初に出現する最大減少部分列に 木[2] を追加する
dp[2] = dp[0](1) + 1 = 2
木[2]が末尾の減少部分列の長さは[0, 2]を選んだ時の2
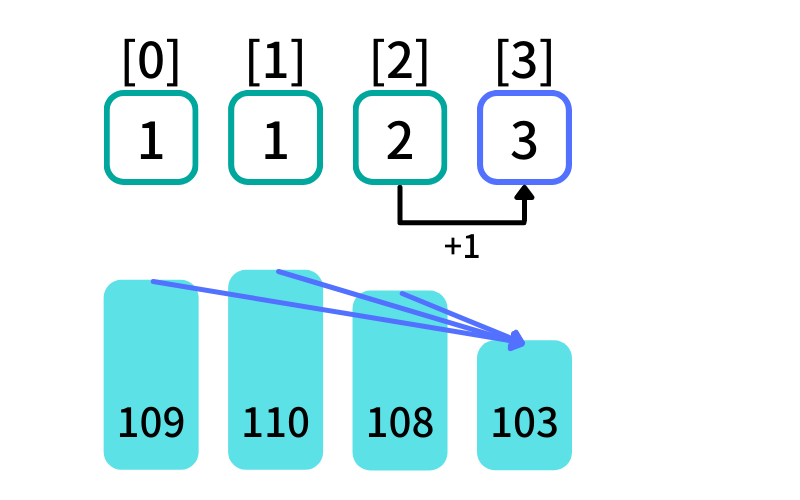
木[3]より手前の項について調べる (i = 3, j = 0, 1, 2)
- 木[0]: dp[0] = 1 , 木[0](109) > 木[3](103) -> True
- 木[1]: dp[1] = 1 , 木[1](110) > 木[3](103) -> True
- 木[2]: dp[2] = 2 , 木[2](108) > 木[3](103) -> True
木[j] > 木[3] を満たし、最初に出現する最大減少部分列に 木[3] を追加する
dp[3] = dp[2](2) + 1 = 3
木[3]が末尾の減少部分列の長さは[0, 2, 3]を選んだ時の3
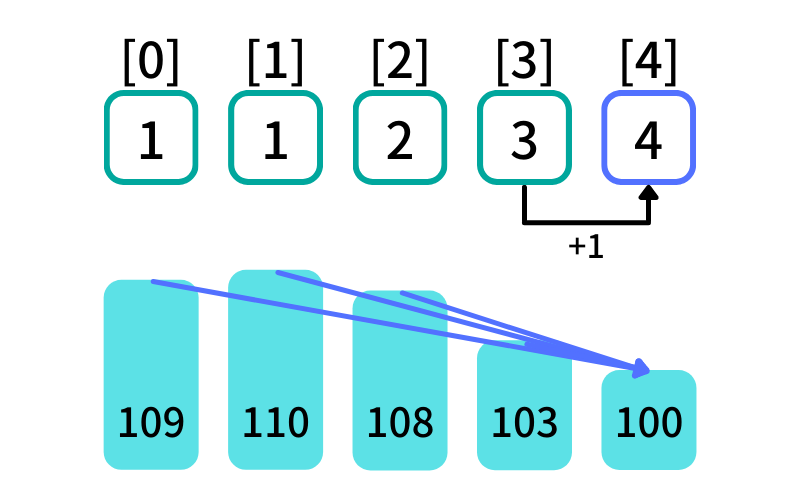
木[4]より手前の項について調べる (i = 4, j = 0, 1, 2, 3)
- 木[0]: dp[0] = 1 , 木[0](109) > 木[4](100) -> True
- 木[1]: dp[1] = 1 , 木[1](110) > 木[4](100) -> True
- 木[2]: dp[2] = 2 , 木[2](108) > 木[4](100) -> True
- 木[3]: dp[3] = 3 , 木[3](103) > 木[4](100) -> True
木[j] > 木[4] を満たし、最初に出現する増加部分列に 木[4] を追加する
dp[4] = dp[3](3) + 1 = 4
木[4]が末尾の減少部分列の長さは[0, 2, 3, 4]を選んだ時の4
- 配列aで減少部分列が最大になる要素の組み合わせは [0, 2, 3, 4](109, 110, 103, 100)
- 配列aで減少部分列が最大になる区間の長さは4
今回のまとめ
セクション5は配列から選択した要素が連続して増加(または減少)する区間の数を求める問題でした。

いきなりこの問題に挑戦すると難しいですが、セクション1から順番に解いてきたらコツがつかめたかと思います!




