paiza グラフ・DFSメニューから、セクション2「パスの通れない頂点 2」を解説します。
セクション2は、セクション1と問題内容がほぼ同じですが、グラフをDFS(深さ優先探索)した経路を列挙する問題となっています。
本記事で使用しているメソッド・アルゴリズムについて
解答例で使っているメソッドやアルゴリズムについて、下記の記事で詳しく解説していますので参考にしてみて下さい。
- [Ruby] 標準入力によるデータ取得1
- [Ruby] 標準入力によるデータ取得2
- [Ruby] 標準入力によるデータ取得3
- [Ruby] 標準出力(データを任意に整形して出力する)
- [Ruby]配列の基本操作1
- [Ruby]繰り返し処理
- [Ruby]ハッシュ(連想配列)
- [アルゴリズム]深さ優先探索・幅優先探索
- [データ構造]スタック・キュー・木構造
セクション1【パスの通れない頂点 2】
STEP1: 隣接頂点の出力 2 (paizaランク D 相当)
ステップ1は、頂点、枝(経路)、頂点 s が与えられ、頂点 s に隣接する頂点の番号を昇順の半角スペース区切りで出力する問題です。
入出力例
1行目で頂点数 n と頂点 s が与えられます。
続く 2 * i 行目には 頂点 i に隣接している頂点の数、 2 * i +1 行目には頂点 i に隣接している頂点番号が半角スペース区切りで与えられます。
INPUT1 = <<~"EOS" 3 2 1 2 2 1 3 1 2 EOS OUTPUT1 = <<~"EOS" 1 3 EOS INPUT2 = <<~"EOS" 5 5 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 1 2 3 4 EOS
INPUT1 はこんな感じ
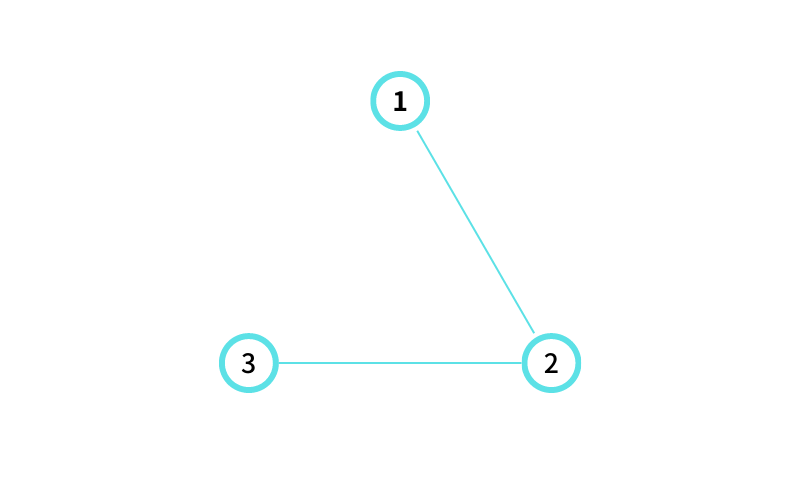
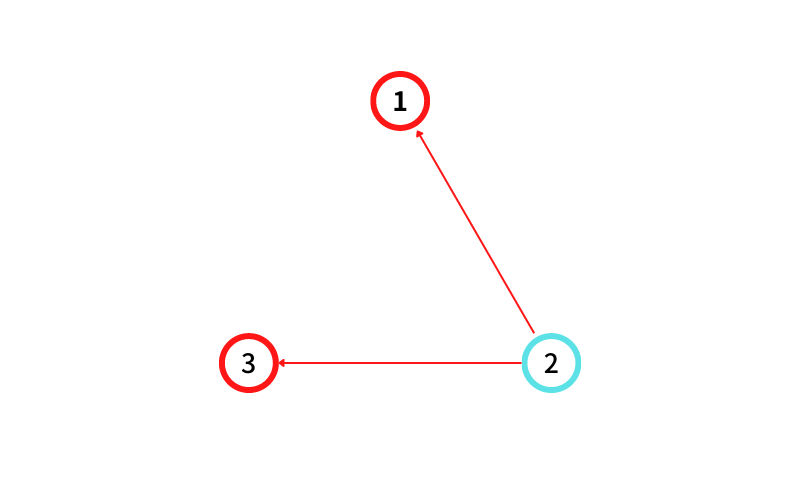
② に隣接する頂点は ① , ③
INPUT2 はこんな感じ
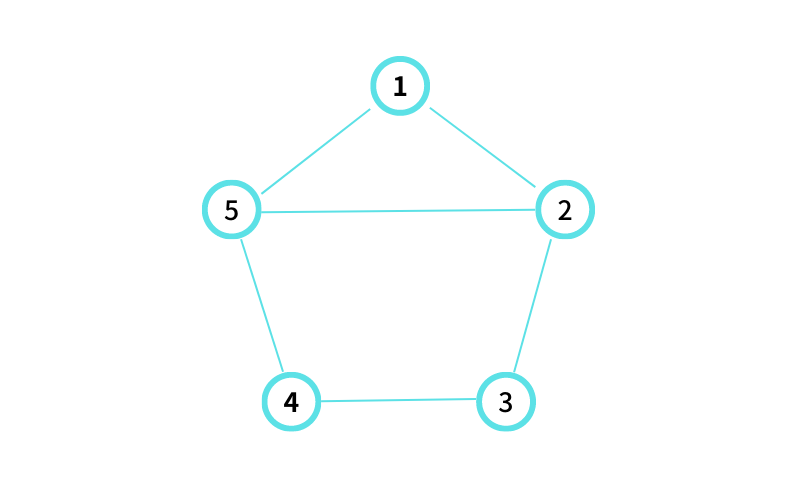
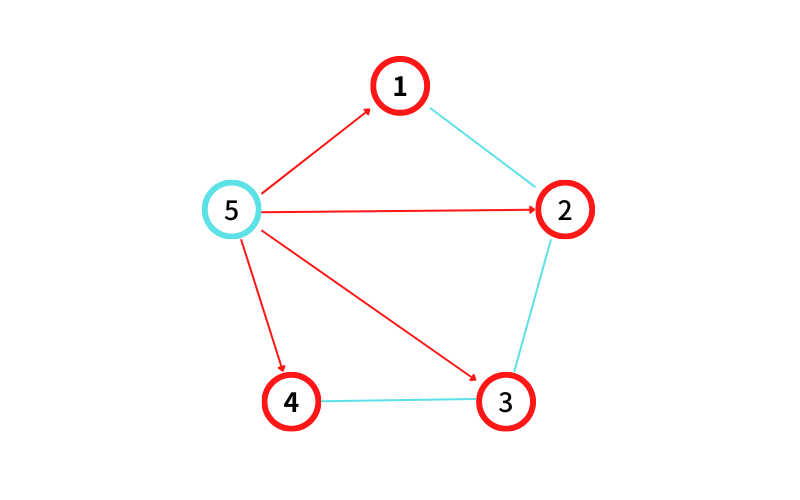
⑤ に隣接する頂点は ①, ②, ③, ④
Ruby 解答例
入力データから隣接リスト ad_list を作成し、ad_list[s] の要素を半角スペースで連結して出力します。
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 探索対象の頂点
n, s = input_lines.shift.split.map(&:to_i)
# 隣接リスト
ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
ad_list[i / 2] = line.split.map(&:to_i)
end
# 頂点 s の隣接頂点を番号順に半角スペース区切りで出力
ad_list[s].join(" ")
end
puts main(STDIN.read)
Python解答例
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 探索対象の頂点
n, s = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# 頂点 s の隣接頂点を番号順に半角スペース区切りで出力
return " ".join(map(str, ad_list[s]))
print(main(open(0).read()))
STEP2: グラフのウォーク 2 (paizaランク C 相当)
ステップ2は、頂点、枝(経路)、起点 s 、移動回数 k が与えられ、 始点 s から k 回移動する経路を全て出力する問題です。
- 頂点を再訪問してもOK (walk)
入出力例
INPUT1 = <<~"EOS" 4 2 4 1 2 3 1 3 4 2 2 4 2 2 3 EOS OUTPUT1 = <<~"EOS" 25 2 1 2 1 2 2 1 2 3 2 2 1 2 3 4 2 1 2 4 2 2 1 2 4 3 2 3 2 1 2 2 3 2 3 2 2 3 2 3 4 2 3 2 4 2 2 3 2 4 3 2 3 4 2 1 2 3 4 2 3 2 3 4 2 4 2 3 4 3 2 2 3 4 3 4 2 4 2 1 2 2 4 2 3 2 2 4 2 3 4 2 4 2 4 2 2 4 2 4 3 2 4 3 2 1 2 4 3 2 3 2 4 3 2 4 2 4 3 4 2 2 4 3 4 3 EOS INPUT2 = <<~"EOS" 5 5 3 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 32 5 1 2 1 5 1 2 3 5 1 2 5 5 1 5 1 5 1 5 2 5 1 5 3 5 1 5 4 5 2 1 2 5 2 1 5 5 2 3 2 5 2 3 4 5 2 3 5 5 2 5 1 5 2 5 2 5 2 5 3 5 2 5 4 5 3 2 1 5 3 2 3 5 3 2 5 5 3 4 3 5 3 4 5 5 3 5 1 5 3 5 2 5 3 5 3 5 3 5 4 5 4 3 2 5 4 3 4 5 4 3 5 5 4 5 1 5 4 5 2 5 4 5 3 5 4 5 4 EOS
INPUT1 はこんな感じ
② からスタートする
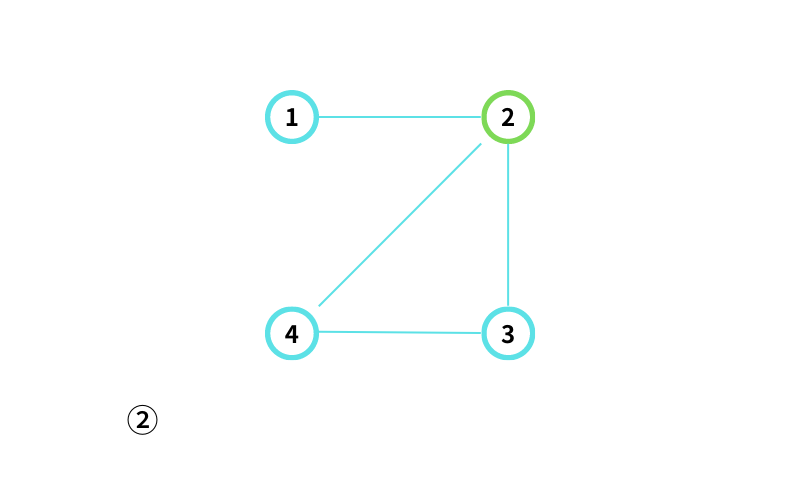
② から ④ に移動する(移動1回目)
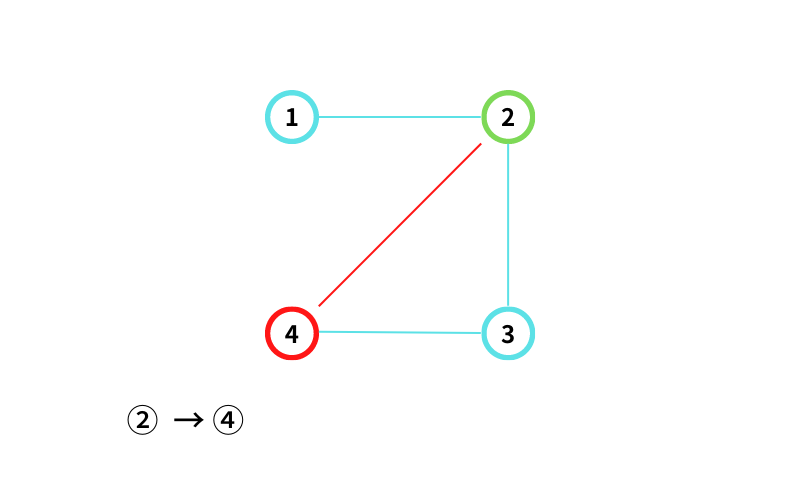
④ から ③ に移動する(移動2回目)
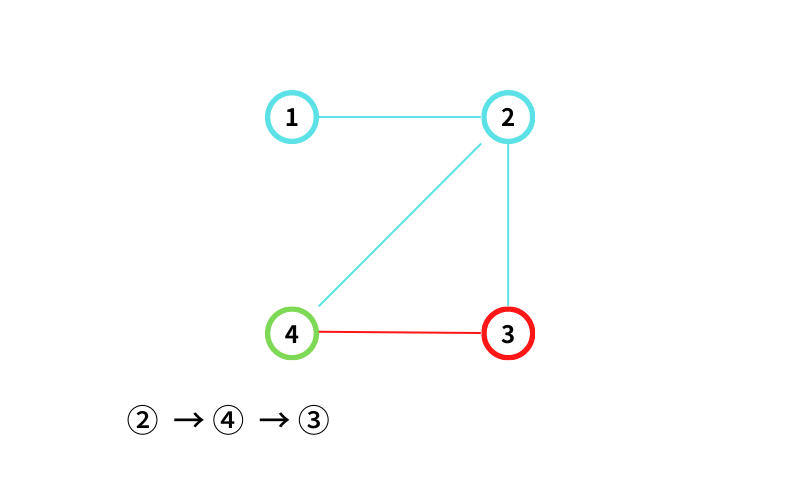
③ から ④ に移動する(移動3回目)
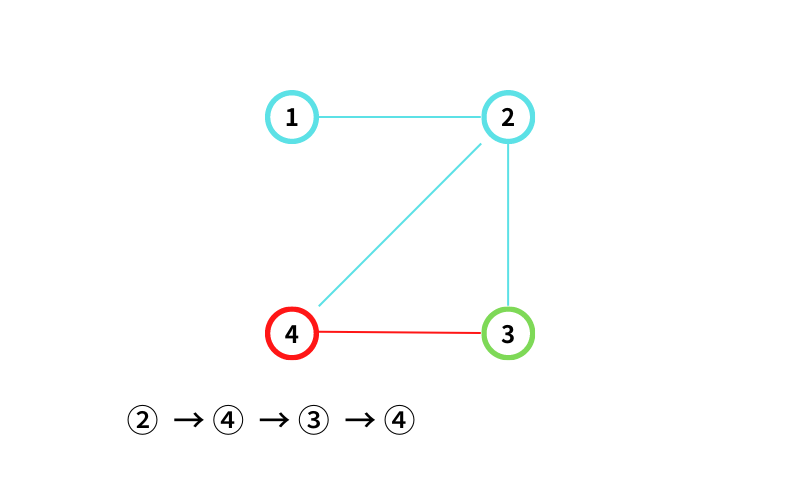
④ から ③ に移動する(移動4回目なので終了)
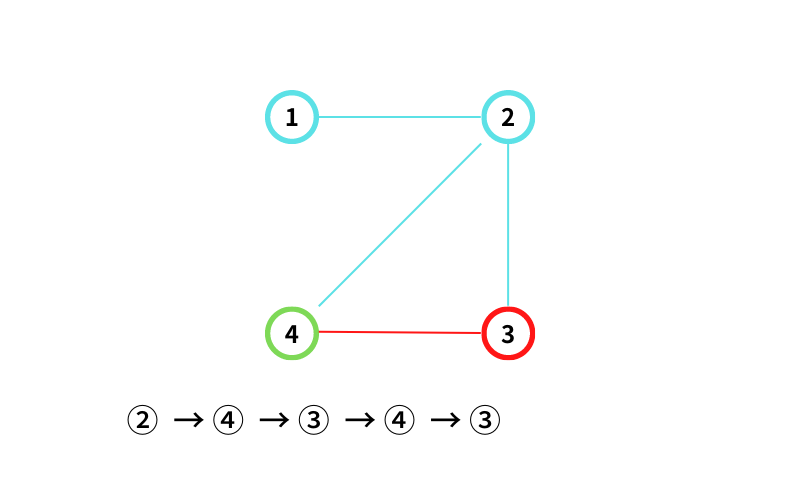
② → ④ → ③ → ④ → ③ という経路(walk)が出来たので記録する。
※ 残りの24経路についても同様に調べる。
INPUT2 はこんな感じ
⑤ からスタートする
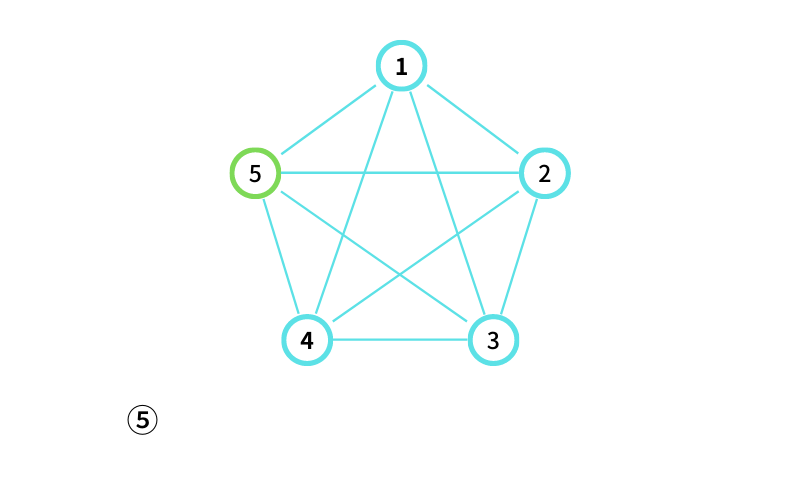
⑤ から ④ に移動する(移動1回目)
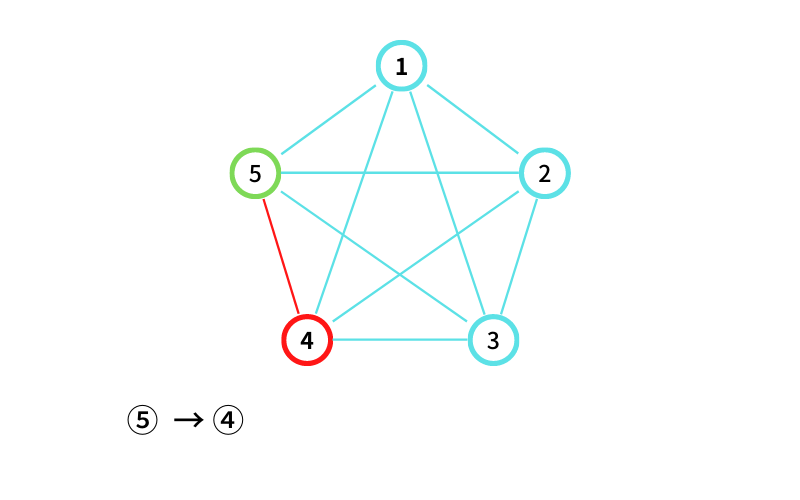
④ から ⑤ に移動する(移動2回目)
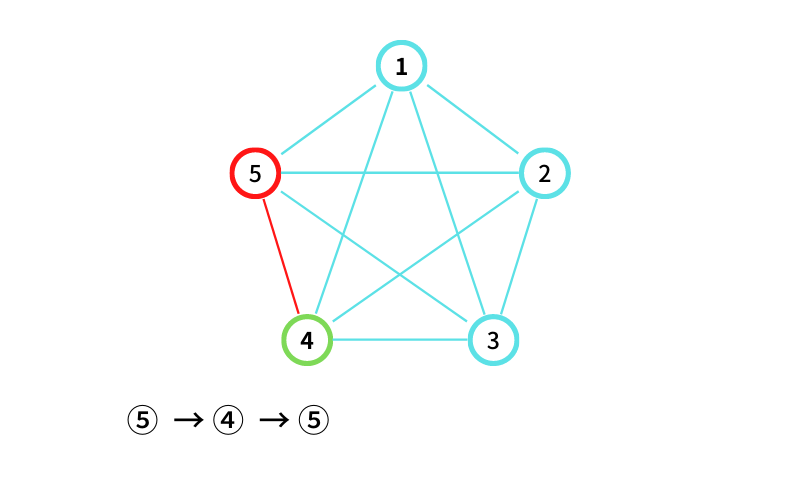
⑤ から ④ に移動する(移動3回目なので終了)
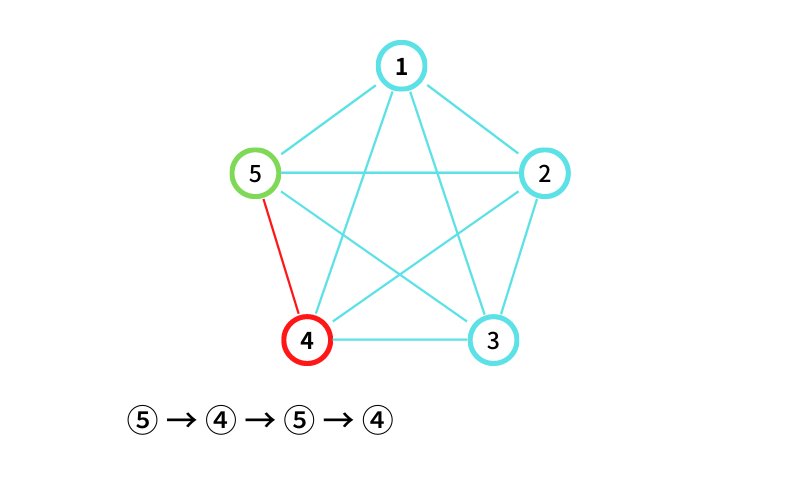
⑤ → ④ → ⑤ → ④ という経路(walk)が出来たので記録する。
※ 残りの31経路についても同様に調べる。
Ruby解答例
以下の流れで実装しています。
- 整数 n, s, k を受け取る
- 隣接リスト ad_list を作成する
- 探索結果 results を空で初期化する
- 探索候補 walks を始点 s で初期化する
- walks が空になるまでループする
- walks 末尾から walk を pop する
- walk の要素数(頂点の数) が k+1 (k 回移動) なら結果を results に記録してスキップ
- cv (最後に訪問した頂点) の隣接リストを nv としてループする
- walk 末尾に nv を加えた経路(walk)を walks 末尾に追加する
- results の各経路(walk)を半角スペース区切りで出力する。
Ruby解答例1 (再帰なし)
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, k: 回数
n, s, k = input_lines.shift.split.map(&:to_i)
# 隣接リスト
ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
ad_list[i / 2] = line.split.map(&:to_i)
end
# k 回移動
results = []
walks = [[s]]
while walks.length > 0
walk = walks.pop
# k 回移動したら経路を記録
if walk.length == k + 1
results << walk
next
end
# 隣接頂点に移動する
cv = walk.last
ad_list[cv].each do |nv|
walks << walk + [nv]
end
end
# 経路数と経路を全て出力
[results.length.to_s].concat(results.map { |e| e.join(" ") }).join("\n")
end
puts main(STDIN.read)
Ruby解答例2 (再帰あり)
def dfs(cv, nodes, k)
if k == 0
# k 回移動したら経路を記録
$results << nodes.dup
else
$ad_list[cv].each do |nv|
# nv を通る
nodes << nv
# 次の層を探索
dfs(nv, nodes, k - 1)
# nv を通らない
nodes.pop
end
end
end
input_str = STDIN.read
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, k: 回数
n, s, k = input_lines.shift.split.map(&:to_i)
# 隣接リスト
$ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
$ad_list[i / 2] = line.split.map(&:to_i)
end
# k 回移動
$results = []
dfs(s, [s], k)
# 経路数と経路を全て出力
puts [$results.length.to_s].concat($results.map { |e| e.join(" ") }).join("\n")
Python解答例1(再帰なし)
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, k: 回数
n, s, k = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# 起点 s から k 回移動する経路
results = []
walks = [[s]]
while len(walks) > 0:
walk = walks.pop()
# k 回移動したら経路を記録
if len(walk) == k + 1:
results.append(walk)
continue
# 隣接頂点に移動する
cv = walk[-1]
for nv in ad_list[cv]:
walks.append(walk + [nv])
# 経路数と経路を全て出力
path_count = str(len(results))
path_list = [" ".join(map(str, res)) for res in results]
return "\n".join([path_count] + path_list)
print(main(open(0).read()))
Python解答例2(再帰あり)
def dfs(cv, nodes, k):
if k == 0:
# k 回移動したら経路を記録
results.append(nodes.copy())
else:
for nv in ad_list[cv]:
# nv を通る
nodes.append(nv)
# 次の層を探索
dfs(nv, nodes, k - 1)
# nv を通らない
nodes.pop()
input_str = open(0).read()
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, k: 回数
n, s, k = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# 起点 s から k 回移動する経路
results = []
dfs(s, [s], k)
# 経路数と経路を全て出力
print(len(results))
[print(*result) for result in results]
STEP3: グラフのパス 2 (paizaランク C 相当)
ステップ3は、頂点数、枝(経路)、起点 s 、移動回数 k が与えられ、 k 回移動した場合の経路を全て出力する問題です。
- 訪問済みの頂点は再訪問できない (path)
入出力例
INPUT1 = <<~"EOS" 4 2 4 1 2 3 1 3 4 2 2 4 2 2 3 EOS OUTPUT1 = <<~"EOS" 0 EOS INPUT2 = <<~"EOS" 5 5 3 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 4 5 1 2 3 5 2 3 4 5 3 2 1 5 4 3 2 EOS INPUT3 = <<~"EOS" 7 1 3 6 2 3 4 5 6 7 2 1 7 2 1 4 2 1 3 2 1 6 2 1 5 2 1 2 EOS OUTPUT3 = <<~"EOS" 0 EOS
INPUT1 はこんな感じ
② からスタートする
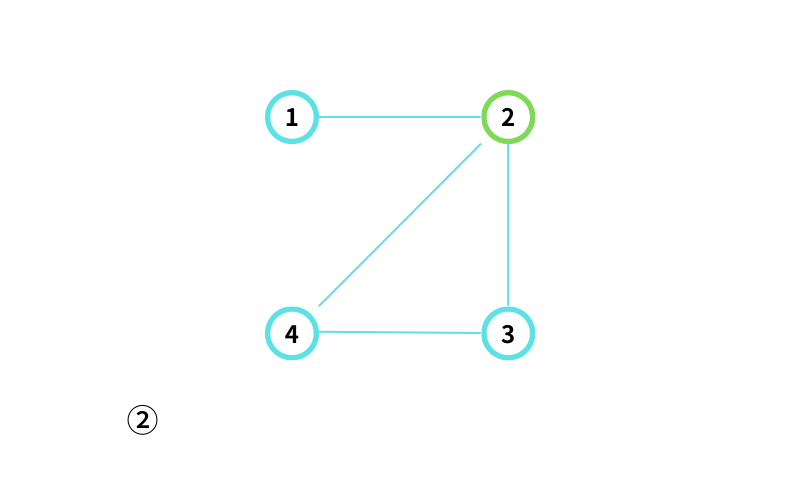
② から ④ に移動する(移動1回目)

④ から ③ に移動する(移動2回目)
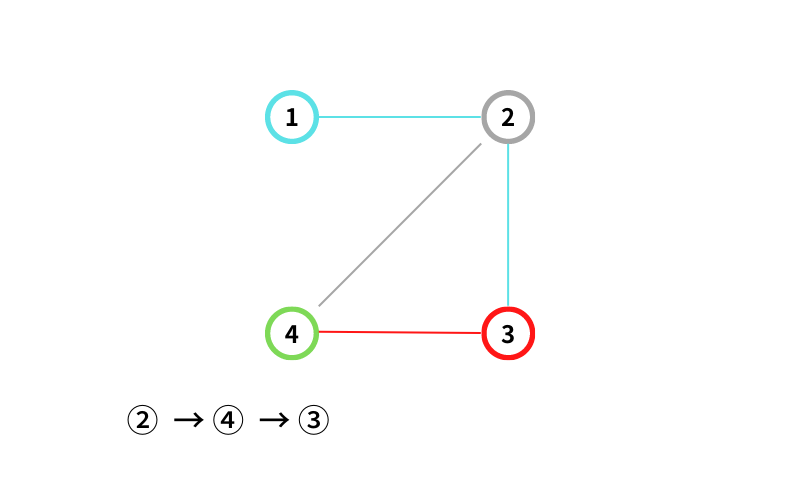
③ からは移動出来ないのでスキップ(探索打ち切り)
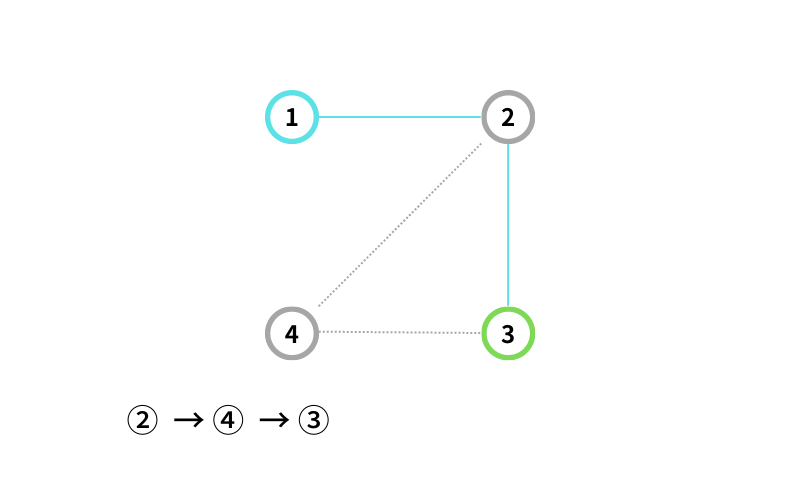
同様に
② → ③ → ④
② → ①
となり、 k 回移動するpathが作れないので -1 を出力する
INPUT2 はこんな感じ
⑤ からスタートする
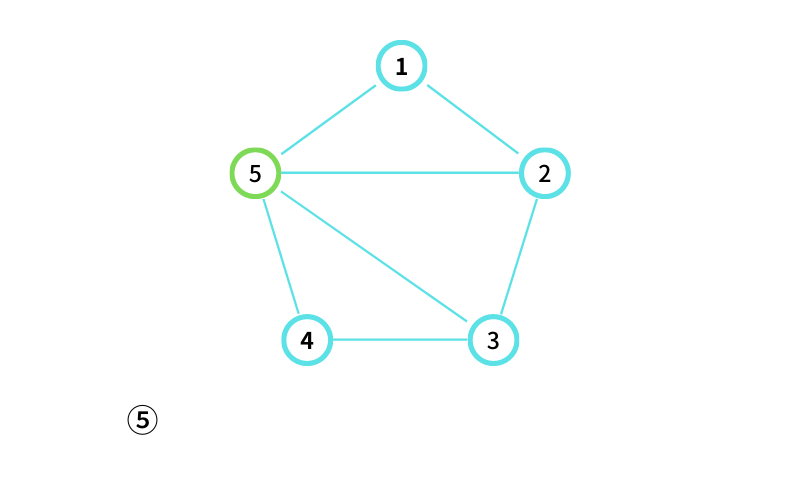
⑤ から ④ に移動する(移動1回目)
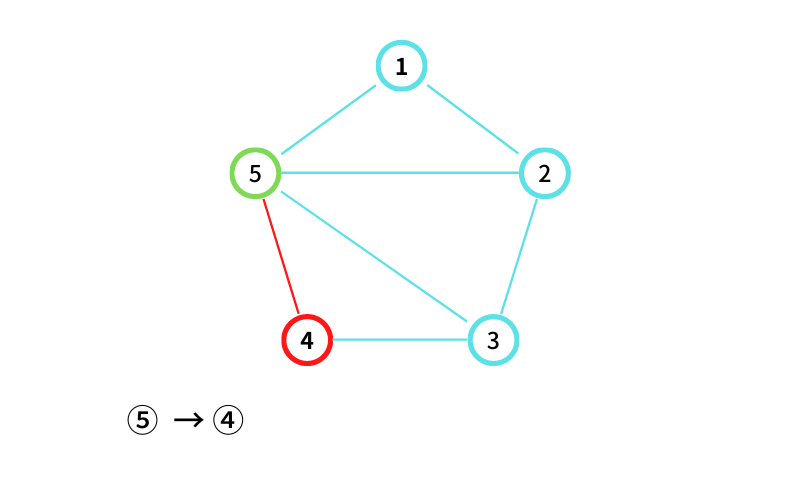
④ から ③ に移動する(移動2回目)
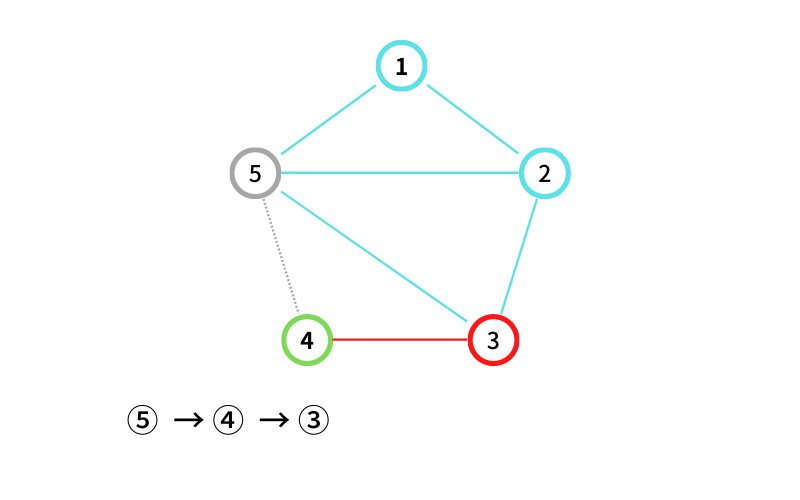
③ から ② に移動する(移動3回目なので終了)
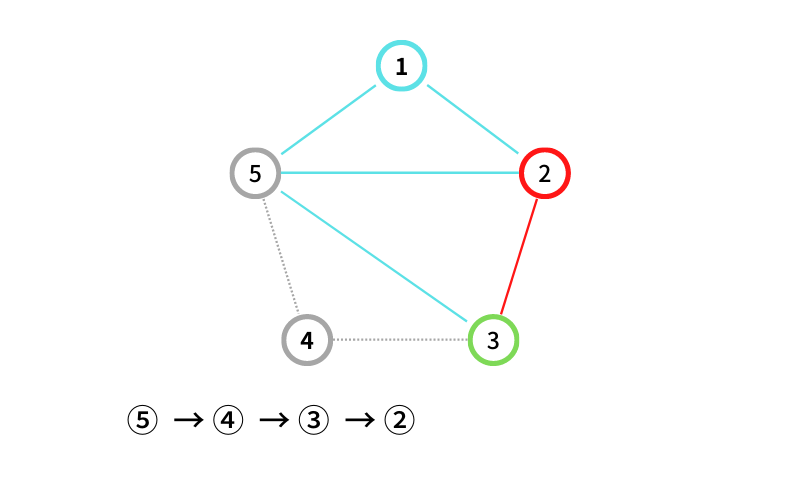
⑤ → ④ → ③ → ② という経路(path)が出来たので記録する。
残りの3経路
⑤ → ③ → ② → ①
⑤ → ② → ③ → ④
⑤ → ① → ② → ③
についても同様に調べる。
Ruby解答例
ステップ2とほぼ同様ですが、次の頂点を加える前に未訪問かを確認しています。
- 整数 n, s, k を受け取る
- 隣接リスト ad_list を作成する
- 探索結果 results を空で初期化する
- 探索候補 paths を始点 s で初期化する
- paths が空になるまでループする
- paths 末尾から path を pop する
- path の要素数(頂点の数) が k+1 (k 回移動) なら結果を results に記録してスキップ
- cv (最後に訪問した頂点) の隣接リストの要素を次の頂点 nv でループする
- 次の頂点 nv が訪問済みならスキップする
- path 末尾に nv を加えた経路(path)を paths 末尾に追加する
- results の各経路(path)を半角スペース区切りで出力する。
Ruby解答例1(再帰なし)
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, k: 回数
n, s, k = input_lines.shift.split.map(&:to_i)
# 隣接リスト
ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
ad_list[i / 2] = line.split.map(&:to_i)
end
# k 回移動
results = []
paths = [[s]]
while paths.length > 0
path = paths.shift
# k 回移動したら経路を記録
if path.length == k + 1
results << path
next
end
# 隣接頂点に移動する
cv = path.last
ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if path.include?(nv)
paths << path + [nv]
end
end
# 経路数と経路を全て出力
[results.length.to_s].concat(results.map { |e| e.join(" ") }).join("\n")
end
puts main(STDIN.read)
Ruby解答例2(再帰あり)
def dfs(cv, nodes, k)
if k == 0
# k 回移動したら経路を記録
$results << nodes.dup
else
$ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if nodes.include?(nv)
# nv を通る
nodes << nv
# 次の層を探索
dfs(nv, nodes, k - 1)
# nv を通らない
nodes.pop
end
end
end
input_str = STDIN.read
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, k: 回数
n, s, k = input_lines.shift.split.map(&:to_i)
# 隣接リスト
$ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
$ad_list[i / 2] = line.split.map(&:to_i)
end
# k 回移動
$results = []
dfs(s, [s], k)
# 経路数と経路を全て出力
puts [$results.length.to_s].concat($results.map { |e| e.join(" ") }).join("\n")
Python解答例1(再帰なし)
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, k: 回数
n, s, k = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# 起点 s から k 回移動する経路
results = []
paths = [[s]]
while len(paths) > 0:
path = paths.pop()
# k 回移動したら経路を記録
if len(path) == k + 1:
results.append(path)
continue
# 隣接頂点に移動する
cv = path[-1]
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in path:
continue
paths.append(path + [nv])
# 経路数と経路を全て出力
path_count = str(len(results))
path_list = [" ".join(map(str, e)) for e in results]
return "\n".join([path_count] + path_list)
print(main(open(0).read()))
Python解答例2(再帰あり)
def dfs(cv, nodes, k):
if k == 0:
# k 回移動したら経路を記録
results.append(nodes.copy())
else:
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in nodes:
continue
# nv を通る
nodes.append(nv)
# 次の層を探索
dfs(nv, nodes, k - 1)
# nv を通らない
nodes.pop()
input_str = open(0).read()
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, k: 回数
n, s, k = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# 起点 s から k 回移動する経路
results = []
dfs(s, [s], k)
# 経路数と経路を全て出力
print(len(results))
[print(*e) for e in results]
STEP4: グラフの s,t パス 2 (paizaランク B 相当)
ステップ4は、頂点、枝(経路)、起点 s 、終点 t が与えられ、 始点 s から 終点 t まで移動できる経路の総数と全ての経路を出力する問題です。
- 同じ頂点は再訪問できない (path)
入出力例
INPUT1 = <<~"EOS" 5 1 4 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT1 = <<~"EOS" 7 1 2 3 4 1 2 3 5 4 1 2 5 3 4 1 2 5 4 1 5 2 3 4 1 5 3 4 1 5 4 EOS INPUT2 = <<~"EOS" 5 5 3 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 4 5 1 2 3 5 2 3 5 3 5 4 3 EOS
INPUT1 はこんな感じ
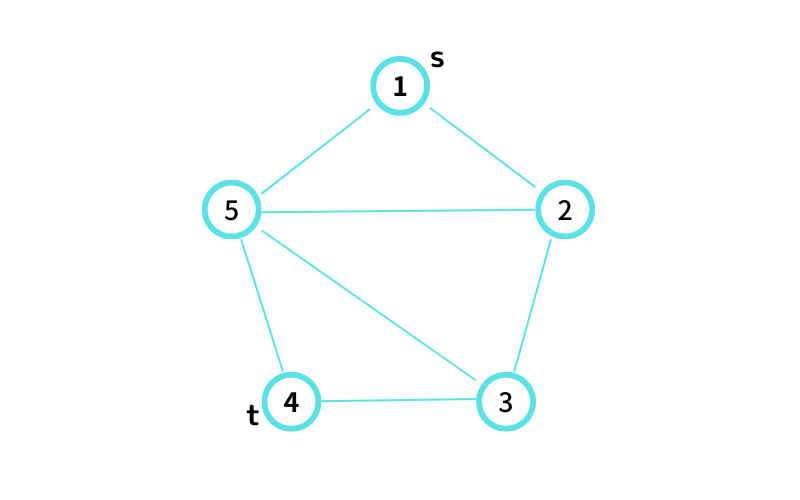
① から ④ へ行ける path は 7 通り
① → ⑤ → ④
① → ⑤ → ③ → ④
① → ⑤ → ② → ③ → ④
① → ② → ⑤ → ④
① → ② → ⑤ → ③ → ④
① → ② → ③ → ⑤ → ④
① → ② → ③ → ④
INPUT2 はこんな感じ
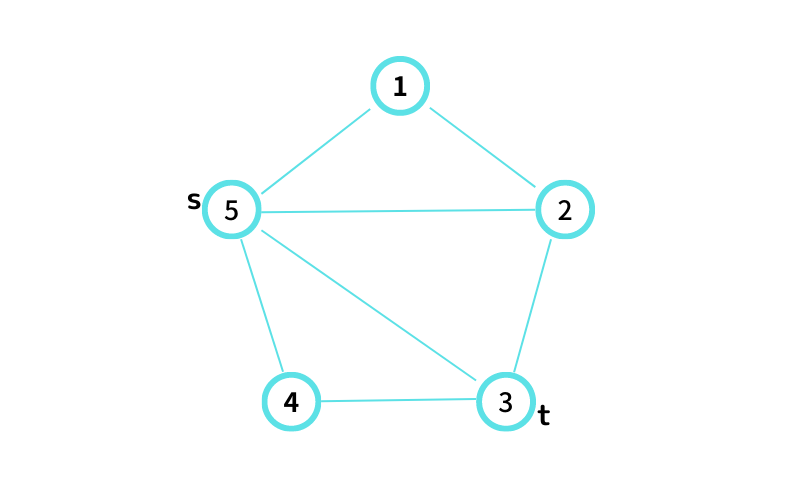
⑤ から ③ へ行ける path は 4 通り
⑤ → ④ → ③
⑤ → ③
⑤ → ② → ③
⑤ → ① → ② → ③
Ruby解答例
ステップ2とほぼ同様ですが、path の末尾が t のときに結果を記録します。
- 整数 n, s, t を受け取る
- 隣接リスト ad_list を作成する
- 探索結果 results を空で初期化する
- 探索候補 paths を始点 s で初期化する
- paths が空になるまでループする
- paths 末尾から path を pop する
- path の末尾要素(最後に訪問した頂点) が t なら結果を results に記録してスキップ
- cv (最後に訪問した頂点) の隣接リストの要素を次の頂点 nv でループする
- 次の頂点 nv が訪問済みならスキップする
- path 末尾に nv を加えた経路(path)を paths 末尾に追加する
- results の各経路(path)を半角スペース区切りで出力する。
Ruby解答例1(再帰なし)
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, t: 終点
n, s, t = input_lines.shift.split.map(&:to_i)
# 隣接リスト
ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
ad_list[i / 2] = line.split.map(&:to_i)
end
# s から t までの経路
results = []
paths = [[s]]
while paths.length > 0
path = paths.pop
# t に着いたら経路を記録
if path.last == t
results << path
next
end
# 隣接頂点に移動する
cv = path.last
ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if path.include?(nv)
paths << path + [nv]
end
end
# 経路数と経路を全て出力
[results.length.to_s].concat(results.map { |e| e.join(" ") }).join("\n")
end
puts main(STDIN.read)
Ruby解答例2(再帰あり)
def dfs(cv, nodes)
$ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if nodes.include?(nv)
# nv を通る
nodes << nv
if nv == $t
# t に着いたら経路を記録
$results << nodes.dup
else
# 次の層を探索
dfs(nv, nodes)
end
# nv を通らない
nodes.pop
end
end
input_str = STDIN.read
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, t: 終点
n, s, $t = input_lines.shift.split.map(&:to_i)
# 隣接リスト
$ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
$ad_list[i / 2] = line.split.map(&:to_i)
end
# s から t までの経路
$results = []
dfs(s, [s])
# 経路数と経路を全て出力
puts [$results.length.to_s].concat($results.map { |e| e.join(" ") }).join("\n")
Python解答例1(再帰なし)
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, t: 終点
n, s, t = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# s から t への経路
results = []
paths = [[s]]
while len(paths) > 0:
path = paths.pop()
# t に着いたら経路を記録
if path[-1] == t:
results.append(path)
continue
# 隣接頂点に移動する
cv = path[-1]
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in path:
continue
paths.append(path + [nv])
# 経路数と経路を全て出力
path_count = str(len(results))
path_list = [" ".join(map(str, e)) for e in results]
return "\n".join([path_count] + path_list)
print(main(open(0).read()))
Python解答例2(再帰あり)
def dfs(cv, nodes):
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in nodes:
continue
# nv を通る
nodes.append(nv)
if nv == t:
# t に着いたら経路を記録
results.append(nodes.copy())
else:
# 次の層を探索
dfs(nv, nodes)
# nv を通らない
nodes.pop()
input_str = open(0).read()
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, t: 終点
n, s, t = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# s から t までの経路
results = []
dfs(s, [s])
# 経路数と経路を全て出力
print(len(results))
[print(*e) for e in results]
STEP5: パスの経由地 2 (paizaランク B 相当)
ステップ5は、頂点、枝(経路)、起点 s 、終点 t 、中継点 q が与えられ、 始点 s から 中継点 q を経由して 終点 t まで移動できる経路の総数と全ての経路を出力する問題です。(※ 本家では中継点 p となっていますが、 p という変数を使いたくないので p → q に変更しました)
・訪問済みの頂点は再訪問できない (path)
・経路が存在しない場合もある
入出力例
INPUT1 = <<~"EOS" 5 1 4 3 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT1 = <<~"EOS" 5 1 2 3 4 1 2 3 5 4 1 2 5 3 4 1 5 2 3 4 1 5 3 4 EOS INPUT2 = <<~"EOS" 5 5 3 1 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 1 5 1 2 3 EOS INPUT3 = <<~"EOS" 8 8 4 1 1 2 7 1 3 4 5 6 7 8 6 2 4 5 6 7 8 6 2 3 5 6 7 8 6 2 3 4 6 7 8 6 2 3 4 5 7 8 6 2 3 4 5 6 8 6 2 3 4 5 6 7 EOS OUTPUT3 = <<~"EOS" 0 EOS
INPUT1 はこんな感じ
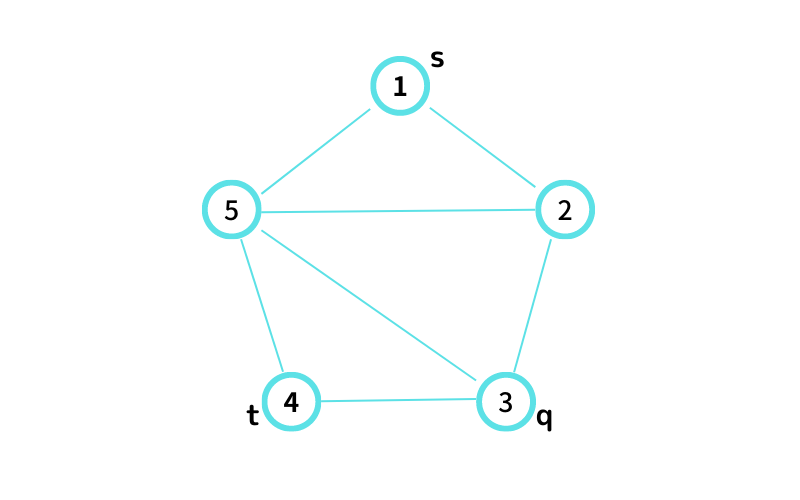
① から ③ を経由して ④ へ行ける path は 5 通り
① → ⑤ → ③ → ④
① → ⑤ → ② → ③ → ④
① → ② → ⑤ → ③ → ④
① → ② → ③ → ⑤ → ④
① → ② → ③ → ④
INPUT2 はこんな感じ
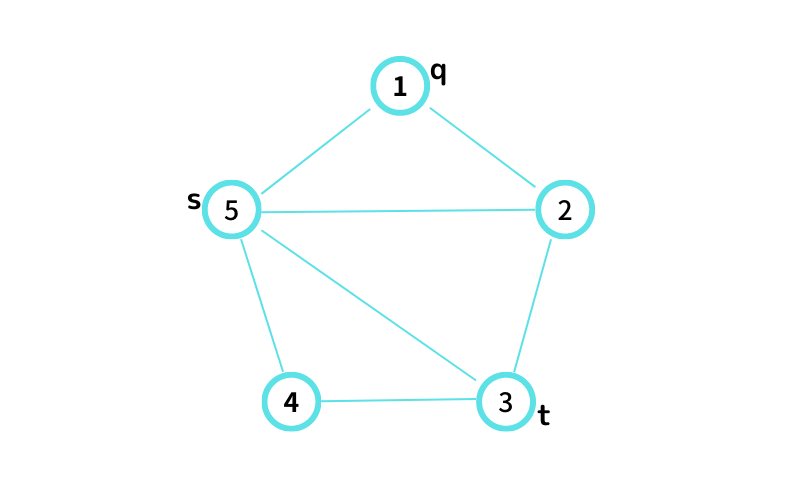
⑤ から ① を経由して ③ へ行ける path は 1 通り
⑤ → ① → ② → ③
INPUT3 はこんな感じ
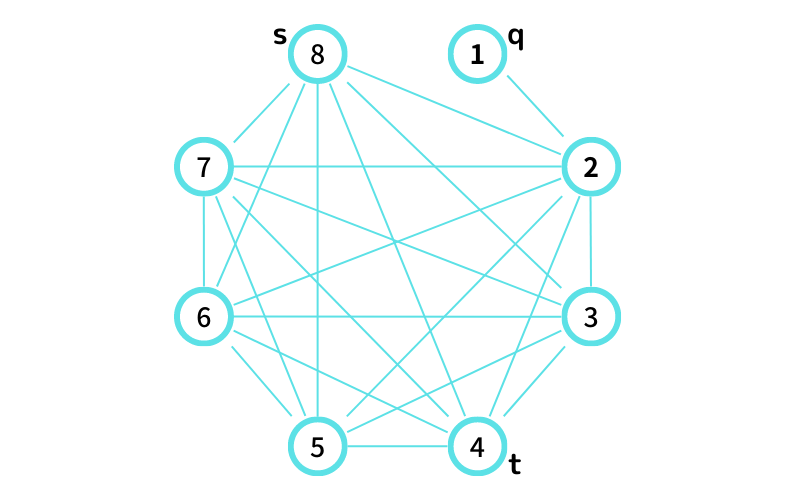
⑧ から ① を経由して ④ へ行ける path は無い
(中継頂点 ① の隣接頂点が1個しかないから)
Ruby解答例
今回も前回のコードを流用します。
path の末尾が t かつ、path に q を含む場合、結果を記録します。
- 整数 n, s, t, q を受け取る
- 隣接リスト ad_list を作成する
- 探索結果 results を空で初期化する
- 探索候補 paths を始点 s で初期化する
- paths が空になるまでループする
- paths 末尾から path を pop する
- path の末尾要素が t かつ、 path に q を含むなら結果を results に記録してスキップ
- cv (最後に訪問した頂点) の隣接リストの要素を次の頂点 nv でループする
- 次の頂点 nv が訪問済みならスキップする
- path 末尾に nv を加えた経路(path)を paths 末尾に追加する
- results の各経路(path)を半角スペース区切りで出力する。
Ruby解答例1(再帰なし)
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, t: 終点, q: 中継点
n, s, t, q = input_lines.shift.split.map(&:to_i)
# 隣接リスト
ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
ad_list[i / 2] = line.split.map(&:to_i)
end
# s → q → t の経路
results = []
paths = [[s]]
while paths.length > 0
path = paths.pop
# q を経由して t に着いたら経路を記録
if path.last == t && path.include?(q)
results << path
next
end
# 隣接頂点に移動する
cv = path.last
ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if path.include?(nv)
paths << path + [nv]
end
end
# 経路数と経路を全て出力
[results.length.to_s].concat(results.map { |e| e.join(" ") }).join("\n")
end
puts main(STDIN.read)
Ruby解答例2(再帰あり)
def dfs(cv, nodes)
$ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if nodes.include?(nv)
# nv を通る
nodes << nv
if nv == $t && nodes.include?($q)
# q を経由して t に着いたら経路を記録
$results << nodes.dup
else
# 次の層を探索
dfs(nv, nodes)
end
# nv を通らない
nodes.pop
end
end
input_str = STDIN.read
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, t: 終点, q: 中継点
n, s, $t, $q = input_lines.shift.split.map(&:to_i)
# 隣接リスト
$ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
$ad_list[i / 2] = line.split.map(&:to_i)
end
# s から t までの経路
$results = []
dfs(s, [s])
# 経路数と経路を全て出力
puts [$results.length.to_s].concat($results.map { |e| e.join(" ") }).join("\n")
Python解答例1(再帰なし)
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, t: 終点, q: 中継点
n, s, t, q = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# s から t への経路
results = []
paths = [[s]]
while len(paths) > 0:
path = paths.pop()
# q を経由して t に着いたら経路を記録
if path[-1] == t and q in path:
results.append(path)
continue
# 隣接頂点に移動する
cv = path[-1]
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in path:
continue
paths.append(path + [nv])
# 経路数と経路を全て出力
path_count = str(len(results))
path_list = [" ".join(map(str, e)) for e in results]
return "\n".join([path_count] + path_list)
print(main(open(0).read()))
Python解答例2(再帰あり)
def dfs(cv, nodes):
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in nodes:
continue
# nv を通る
nodes.append(nv)
if nv == t and q in nodes:
# q を経由して t に着いたら経路を記録
results.append(nodes.copy())
else:
# 次の層を探索
dfs(nv, nodes)
# nv を通らない
nodes.pop()
input_str = open(0).read()
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, t: 終点, q: 中継点
n, s, t, q = map(int, input_lines[0].split())
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[1:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# s から t までの経路
results = []
dfs(s, [s])
# 経路数と経路を全て出力
print(len(results))
[print(*e) for e in results]
FINAL: パスの通れない頂点 2 (paizaランク B 相当)
ステップ6は、頂点、枝(経路)、訪問出来ない頂点、起点 s 、終点 t が与えられ、 始点 s から 終点 t まで移動できる経路の総数と全ての経路を出力する問題です
- 訪問済みの頂点は再訪問できない (path)
- 経路が存在しない場合もある
入出力例
INPUT1 = <<~"EOS" 5 1 4 3 2 3 5 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT1 = <<~"EOS" 0 EOS INPUT2 = <<~"EOS" 5 5 3 3 1 2 4 2 2 5 3 1 3 5 3 2 4 5 2 3 5 4 1 2 3 4 EOS OUTPUT2 = <<~"EOS" 1 5 3 EOS INPUT3 = <<~"EOS" 7 3 4 1 2 6 2 3 4 5 6 7 3 1 3 7 3 1 2 4 3 1 3 5 3 1 4 6 3 1 5 7 3 1 2 6 EOS OUTPUT3 = <<~"EOS" 5 3 1 4 3 1 5 4 3 1 6 5 4 3 1 7 6 5 4 3 4 EOS
INPUT1 はこんな感じ
通れない頂点: ②, ③, ⑤
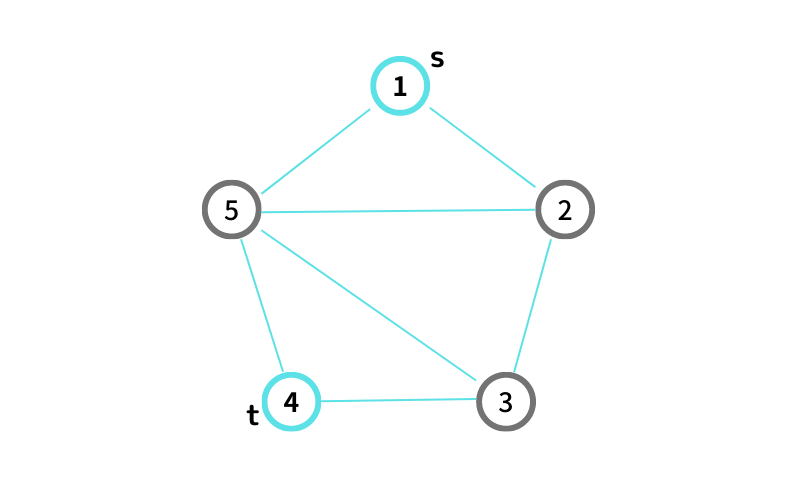
① から ④ へ行ける path は無い
INPUT2 はこんな感じ
通れない頂点: ①, ②, ④
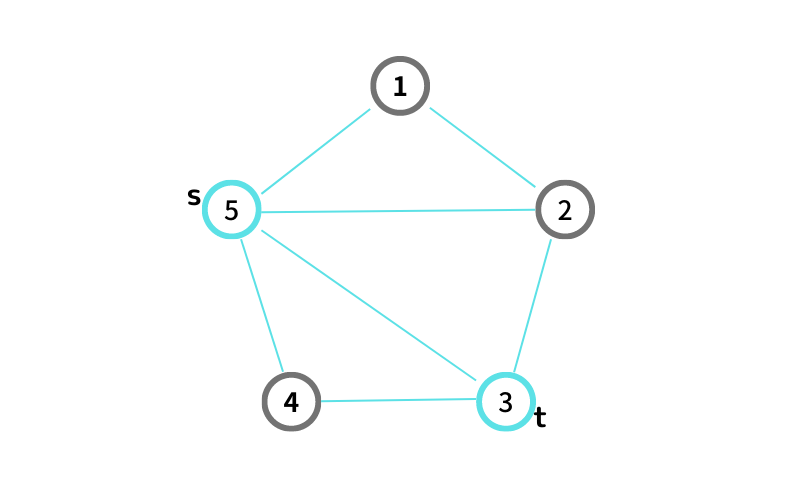
⑤ から ③ へ行ける path は 1 通り
⑤ → ③
INPUT3 はこんな感じ
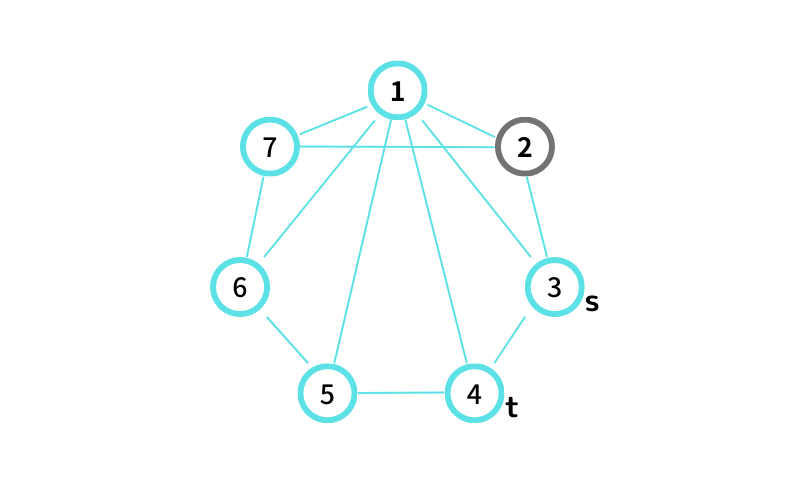
③ から ④ へ行ける path は 5 通り
③ → ④
③ → ① → ⑦ → ⑥ → ⑤ → ④
③ → ① → ⑥ → ⑤ → ④
③ → ① → ⑤ → ④
③ → ① → ④
Ruby解答例
ステップ4のコードを流用します。
訪問しない頂点を配列で記録しておき、探索候補の頂点が訪問しない頂点ならスキップする条件分岐を追加します。
- 整数 n, s, t を受け取る
- 隣接リスト ad_list を作成する
- 通らない頂点のリスト unused_vertices を作成する
- 探索結果 results を空で初期化する
- 探索候補 paths を始点 s で初期化する
- paths が空になるまでループする
- paths 末尾から path を pop する
- path の末尾要素(最後に訪問した頂点) が t なら結果を results に記録してスキップ
- cv (最後に訪問した頂点) の隣接リストの要素を次の頂点 nv でループする
- 次の頂点 nv が訪問済みならスキップする
- 次の頂点 nv が unused_vertices に含まれているならスキップする
- path 末尾に nv を加えた経路(path)を paths 末尾に追加する
- results の各経路(path)を半角スペース区切りで出力する。
Ruby解答例1(再帰なし)
def main(input_str)
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, t: 終点
n, s, t = input_lines.shift.split.map(&:to_i)
# 通らない頂点
unused_vertices = input_lines.shift(2).last.split.map(&:to_i)
# 隣接リスト
ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
ad_list[i / 2] = line.split.map(&:to_i)
end
# 始点 s から終点 t までの経路
results = []
paths = [[s]]
while paths.length > 0
path = paths.pop
# t に着いたら経路を記録
if path.last == t
results << path
next
end
# 未訪問の隣接頂点に移動する
cv = path.last
ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if path.include?(nv)
# 通れない頂点はスキップ
next if unused_vertices.include?(nv)
paths << path + [nv]
end
end
# 経路数と経路を全て出力
[results.length.to_s].concat(results.map { |e| e.join(" ") }).join("\n")
end
puts main(STDIN.read)
Ruby解答例2(再帰あり)
def dfs(cv, nodes)
$ad_list[cv].each do |nv|
# 訪問済の頂点はスキップ
next if nodes.include?(nv)
# 通れない頂点はスキップ
next if $unused_vertices.include?(nv)
# nv を通る
nodes << nv
if nv == $t
# t に着いたら経路を記録
$results << nodes.dup
else
# 次の層を探索
dfs(nv, nodes)
end
# nv を通らない
nodes.pop
end
end
input_str = STDIN.read
input_lines = input_str.split("\n")
# n: 頂点数, s: 起点, t: 終点
n, s, $t = input_lines.shift.split.map(&:to_i)
# 通らない頂点
$unused_vertices = input_lines.shift(2).last.split.map(&:to_i)
# 隣接リスト
$ad_list = {}
input_lines.each.with_index(1) do |line, i|
next if i.odd?
$ad_list[i / 2] = line.split.map(&:to_i)
end
# s から t までの経路
$results = []
dfs(s, [s])
# 経路数と経路を全て出力
puts [$results.length.to_s].concat($results.map { |e| e.join(" ") }).join("\n")
Python解答例1(再帰なし)
def main(input_str):
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, t: 終点
n, s, t = map(int, input_lines[0].split())
# 通らない頂点
unused_vertices = list(map(int, input_lines[2].split()))
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[3:], 1):
# 経路数 v は使わない
if i % 2 == 0:
# 隣接リストに経路を格納
ad_list[i // 2] = list(map(int, line.split()))
# 始点 s から終点 t までの経路
results = []
paths = [[s]]
while len(paths) > 0:
path = paths.pop()
# t に着いたら経路を記録
if path[-1] == t:
results.append(path)
continue
# 未訪問の隣接頂点に移動する
cv = path[-1]
for nv in ad_list[cv]:
# 訪問済の頂点と通れない頂点はスキップ
if nv in path or nv in unused_vertices:
continue
# 新しい経路を追加
paths.append(path + [nv])
# 経路数と経路を全て出力
path_count = str(len(results))
path_list = [" ".join(map(str, e)) for e in results]
return "\n".join([path_count] + path_list)
print(main(open(0).read()))
Python解答例2(再帰あり)
def dfs(cv, nodes):
for nv in ad_list[cv]:
# 訪問済の頂点はスキップ
if nv in nodes:
continue
# 通れない頂点はスキップ
if nv in unused_vertices:
continue
# nv を通る
nodes.append(nv)
if nv == t:
# t に着いたら経路を記録
results.append(nodes.copy())
else:
# 次の層を探索
dfs(nv, nodes)
# nv を通らない
nodes.pop()
input_str = open(0).read()
input_lines = input_str.splitlines()
# n: 頂点数, s: 起点, t: 終点
n, s, t = map(int, input_lines[0].split())
# 通らない頂点
unused_vertices = list(map(int, input_lines[2].split()))
# 隣接リスト
ad_list = {}
for (i, line) in enumerate(input_lines[3:], 1):
if i % 2 != 0:
continue
ad_list[i // 2] = list(map(int, line.split()))
# s から t までの経路
results = []
dfs(s, [s])
# 経路数と経路を全て出力
print(len(results))
[print(*e) for e in results]
今回のまとめ
- DFS(深さ優先探索)の基本部分の構造はだいたい一緒
- スキップ条件、探索終了条件を変えることで色々な問題に対応できる
- ウォーク (walk) は頂点の反復を許す経路
- パス (path) は頂点の反復を許さない経路

今回は、別解として再帰呼び出しのコードも記載してみました。
セクション3からは、新しい経路の種類 トレイル (trail) を扱います!




