累積和とは
累積和(prefix sum)は、配列の任意の区間の総和を求めるためのアルゴリズムです。
繰り返し処理を使うと大きな計算量になってしまう区間の計算問題を、適切な前処理を行うことによって高速に行うことができます。
配列の累積和を求める
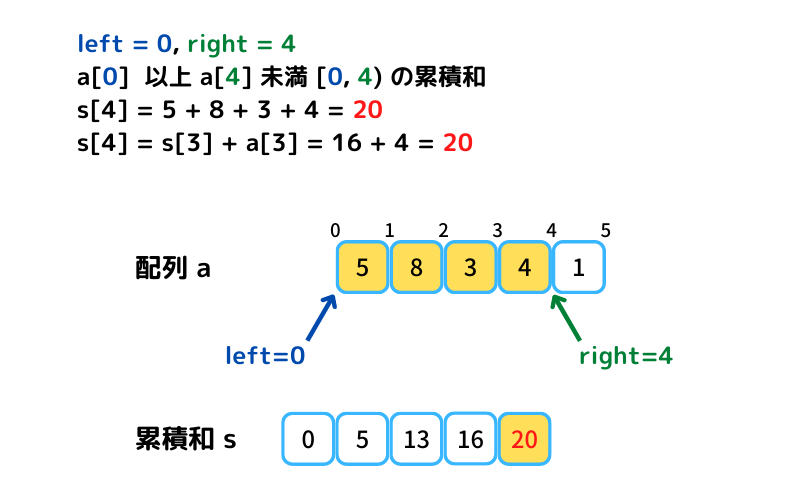
まずはサンプル配列a=[5, 8, 3, 4, 1]の累積和sを求めてみます。
この処理を行うことで任意区間の和を簡単に求めることが出来るようになります。
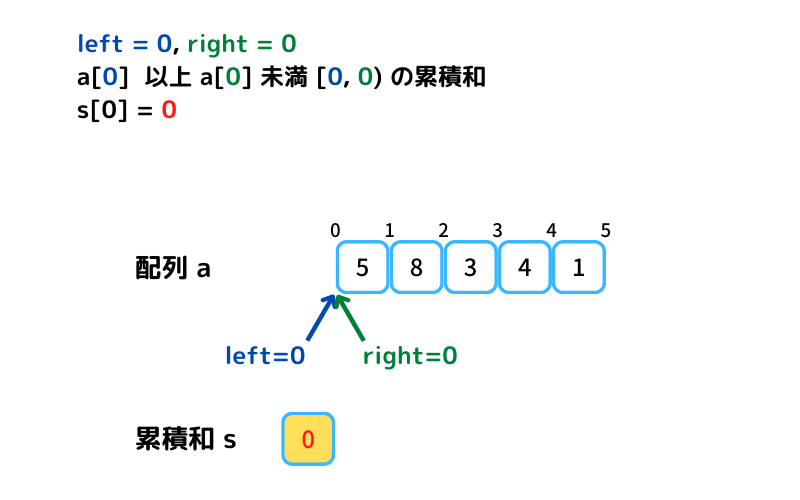
累積和の計算 サンプルコード1
a[left] 以上 a[right] 未満の累積和の計算を愚直に書くと以下のようになります。
コードは読み易いですが、計算量がちょっとヘビーになります。計算量O(n*n)
# 累積和の計算1 a = [5, 8, 3, 4, 1] n = a.length left = 0 s = [] 0.upto(n) do |right| s << a[left...right].sum end p s #> [0, 5, 13, 16, 20, 21]
累積和の計算 サンプルコード2
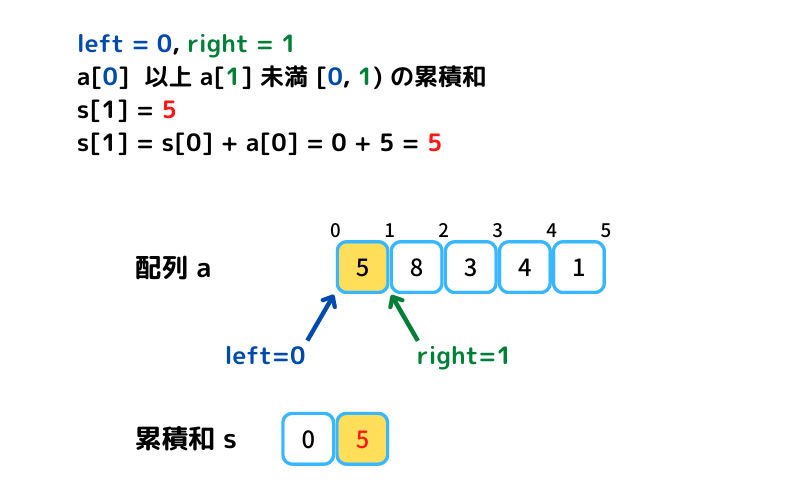
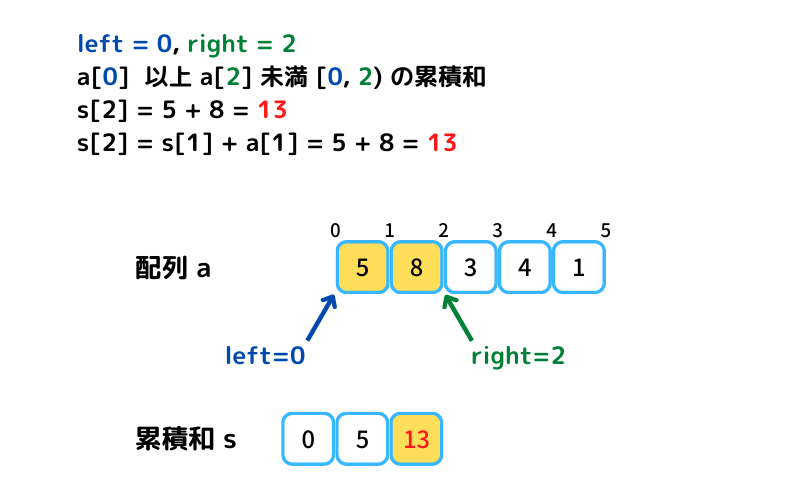
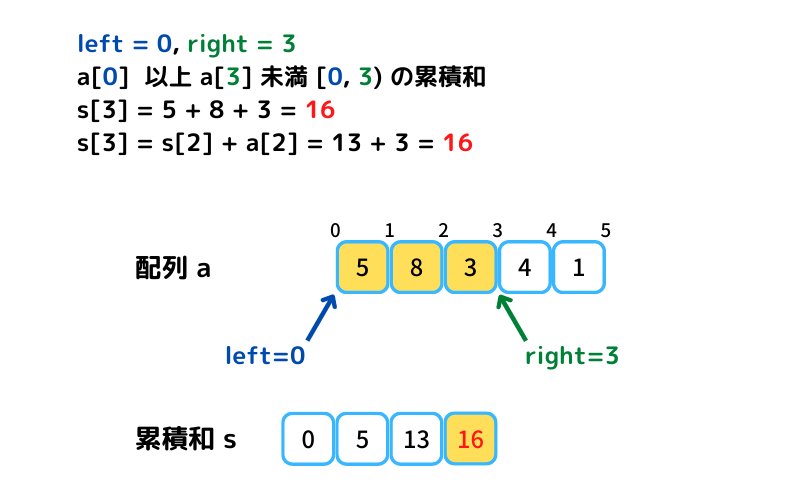
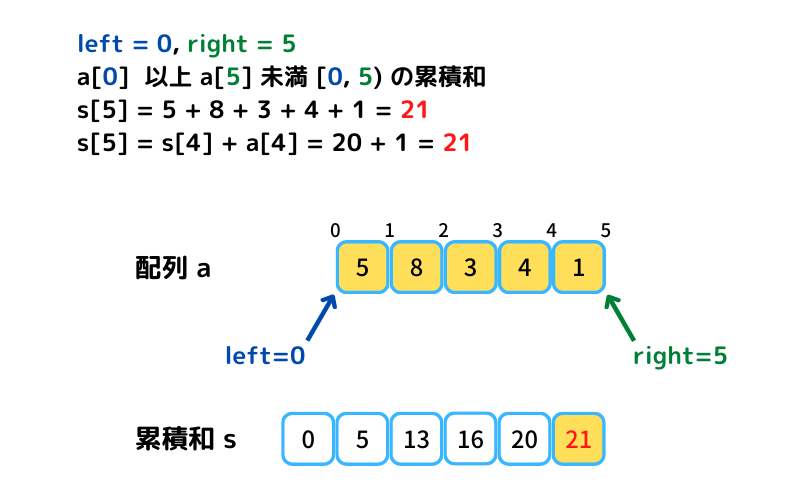
a[left=0] 以上 a[right=0] 未満の区間和 s[0] を初期値として、
s[i+1] = s[i] + a[i] で累計和を求めることもできます。計算量O(n)
# 累積和の計算2 a = [5, 8, 3, 4, 1] s = [0] a.each do |a_i| s << s[-1] + a_i end p s #> [0, 5, 13, 16, 20, 21]
配列の区間和を求める
配列aの累積和sを求めたので、累積和sを使って、配列aの任意の区間和を1回の引き算で求めることが出来るようになりました。
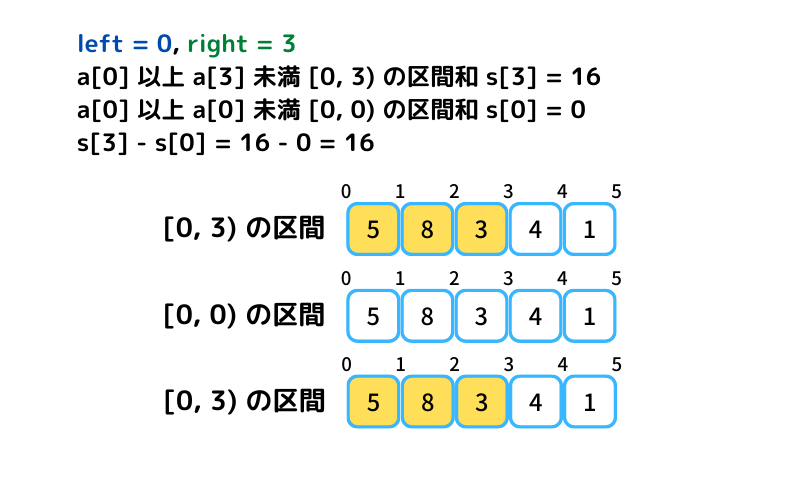


区間和の計算 サンプルコード
# 区間和の計算 a = [5, 8, 3, 4, 1] n = a.length s = [0] a.each do |a_i| s << s[-1] + a_i end p s #> [0, 5, 13, 16, 20, 21] # a[0] 以上 a[3] 未満 [0, 3) の区間和 p s[3] - s[0] # > 16 # a[1] 以上 a[4] 未満 [1, 4) の区間和 p s[4] - s[1] # > 15 # a[2] 以上 a[5] 未満 [2, 5) の区間和 p s[5] - s[2] # > 8
累積和とループ(sumメソッド)を比べてみる
要素数が数個程度だとメリットが分かりづらいですが、扱う要素数が大きくなるほど、また、計算する重複区間が大きくなるほど効果を発揮します。
試しに要素数100,000で、0から99までのランダムな整数の要素を持つ配列aを用意し、連続する50,000区間の最大和を計算してみます。
累積和を使ったサンプルコード
処理時間: 0.0168849秒
比較や出力を除いた主要部分の計算回数:150,002回
(累積和の計算回数: 100,001回、連続する50,000区間の計算: 50,001回)
srand(0)
a = Array.new(100000) { rand(100) }
# 計測スタート
start = Time.now
# 累積和の計算
s = [0]
a.each do |v|
s << s[-1] + v
end
# 【連続する50000個の最大区間和を求める】
max_sum = -1
# i=0 から 100000-50000=50000 でループ
0.upto(100000 - 50000) do |i|
# i 以上 i+50000 未満 の区間和を求める
section_sum = s[i + 50000] - s[i]
# 最大区間和の更新
max_sum = [max_sum, section_sum].max
end
# 出力
puts max_sum
# 計測終了
finish = Time.now
puts "---"
puts "処理時間: #{finish - start}"
# > 2481910
# > ---
# > 処理時間: 0.0168849
sumメソッドを使ったサンプルコード
処理時間: 4.9138133秒
比較や出力を除いた主要部分の計算回数:2,500,050,000 回
(連続する50,000区間の計算: 50,001 × 50,000 = 2,500,050,000 回)
srand(0)
a = Array.new(100000) { rand(100) }
# 計測スタート
start = Time.now
# 【連続する50000個の最大区間和を求める】
max_sum = -1
# i=0 から 100000-50000=50000 でループ
0.upto(100000 - 50000) do |i|
# i 以上 i+50000 未満 の区間和を求める
section_sum = a[i...i + 50000].sum
# 最大区間和の更新
max_sum = [max_sum, section_sum].max
end
# 出力
puts max_sum
# 計測終了
finish = Time.now
puts "---"
puts "計算回数: #{calc_count}"
puts "処理時間: #{finish - start}"
# > 2481910
# > ---
# > 処理時間: 4.9138133
二次元配列の累積和を求める
二次元配列 a = [[1, 2, 3, 4],[5, 6, 7, 8],[8, 7, 6, 5],[4, 3, 2, 1]] の累積和を求めてみます。
(二次元配列の累積和を求めるときには重複区間に注意。)
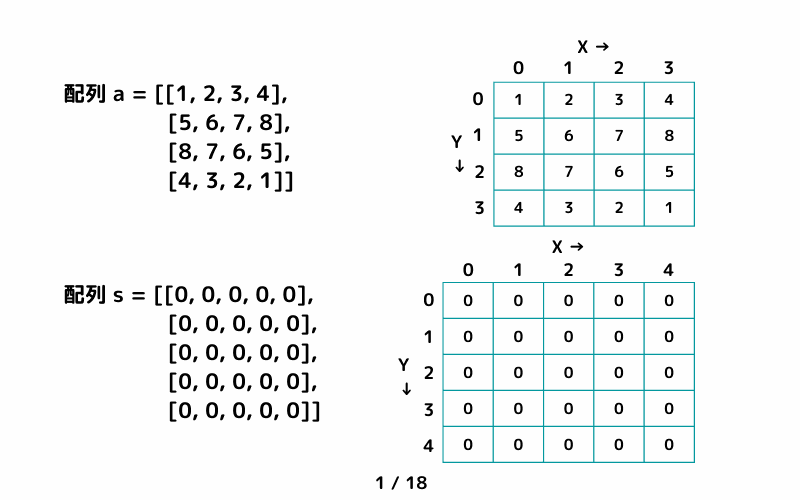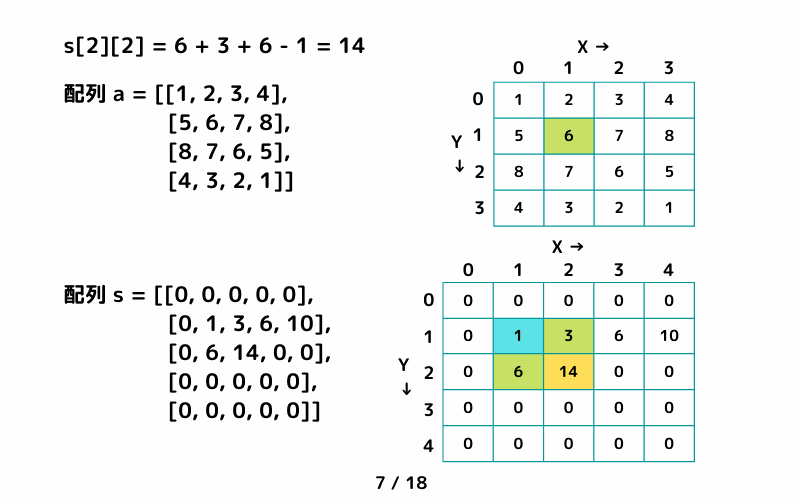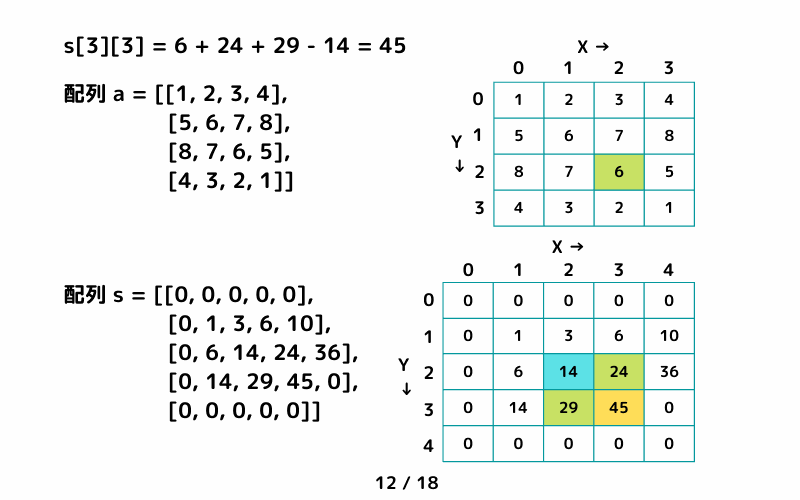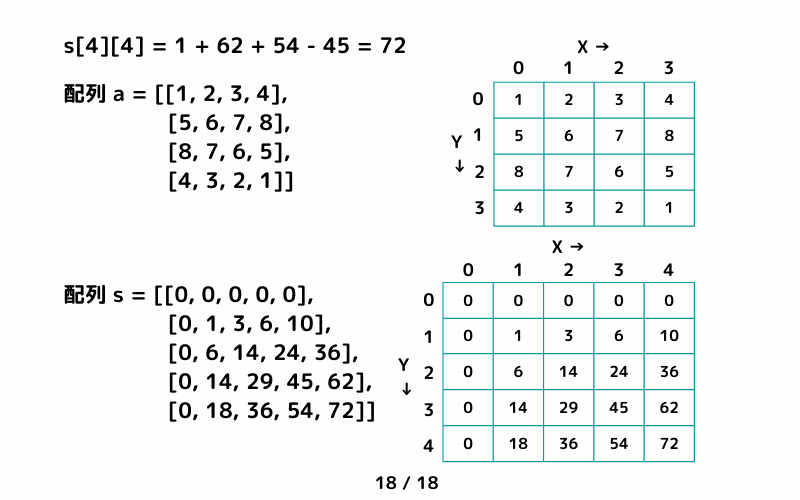
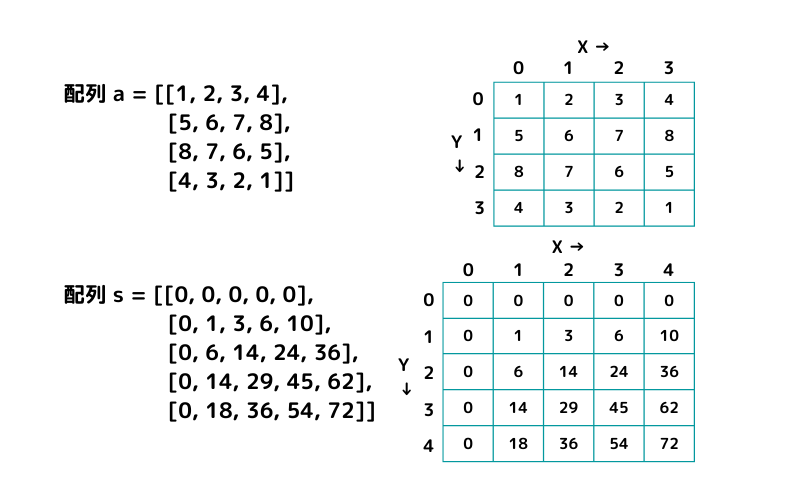
二次元配列の累積和 サンプルコード
h, w = 4, 4
a = [[1, 2, 3, 4],
[5, 6, 7, 8],
[8, 7, 6, 5],
[4, 3, 2, 1]]
# 二次元累積和の計算
s = Array.new(h + 1) { Array.new(w + 1, 0) }
0.upto(h - 1) do |y|
0.upto(w - 1) do |x|
s[y + 1][x + 1] = a[y][x] + s[y][x + 1] + s[y + 1][x] - s[y][x]
end
end
pp s
# > [[ 0, 0, 0, 0, 0],
# > [ 0, 1, 3, 6, 10],
# > [ 0, 6, 14, 24, 36],
# > [ 0, 14, 29, 45, 62],
# > [ 0, 18, 36, 54, 72]]
二次元配列の区間和を求める
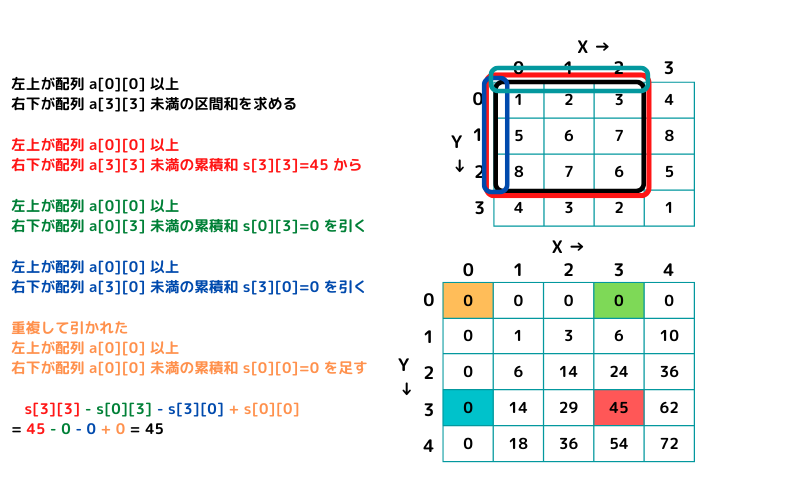
- 左上が a[0][0] 以上 右下が a[3][3] 未満 の黒枠範囲の区間和を求める
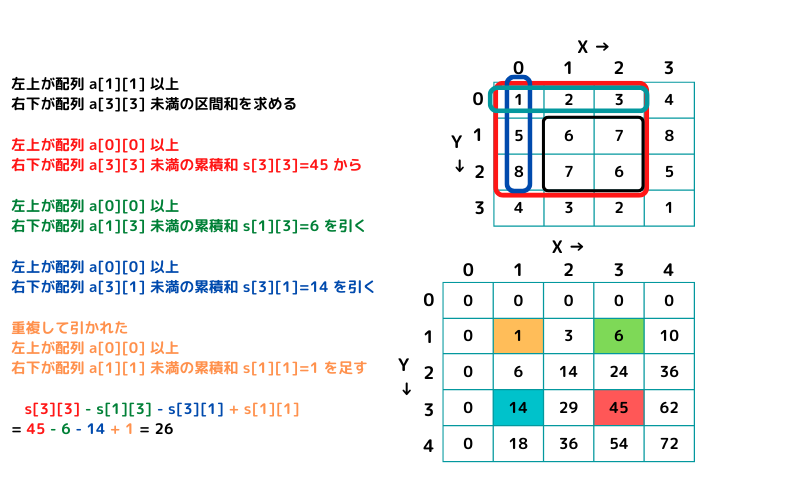
- 左上が a[1][1] 以上 右下が a[3][3] 未満 の黒枠範囲の区間和を求める
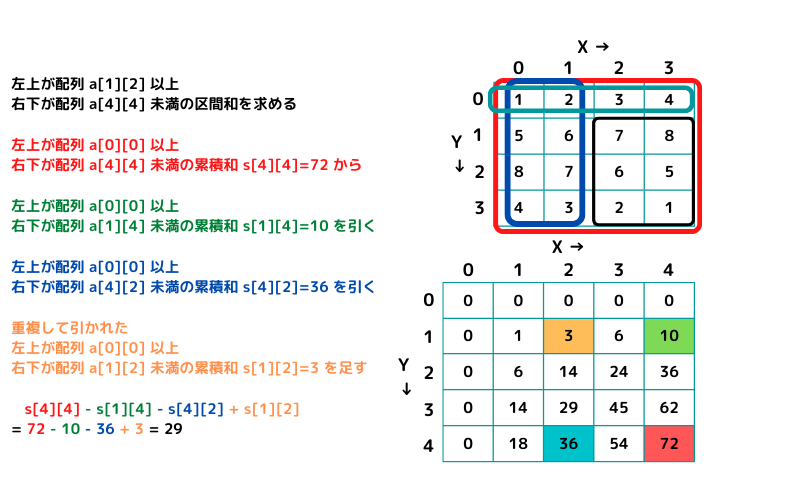
- 左上が a[1][2] 以上 右下が a[4][4] 未満 の黒枠範囲の区間和を求める
二次元配列の区間和 サンプルコード
h, w = 4, 4
a = [[1, 2, 3, 4],
[5, 6, 7, 8],
[8, 7, 6, 5],
[4, 3, 2, 1]]
# 二次元累積和の計算
s = Array.new(h + 1) { Array.new(w + 1, 0) }
0.upto(h - 1) do |y|
0.upto(w - 1) do |x|
s[y + 1][x + 1] = a[y][x] + s[y][x + 1] + s[y + 1][x] - s[y][x]
end
end
pp s
# > [[ 0, 0, 0, 0, 0],
# > [ 0, 1, 3, 6, 10],
# > [ 0, 6, 14, 24, 36],
# > [ 0, 14, 29, 45, 62],
# > [ 0, 18, 36, 54, 72]]
# 左上が a[0][0] 以上 右下が a[3][3] 未満 の区間和
p s[3][3] - s[0][3] - s[3][0] + s[0][0]
# > 45
# 左上が a[1][1] 以上 右下が a[3][3] 未満 の区間和
p s[3][3] - s[1][3] - s[3][1] + s[1][1]
# > 26
# 左上が a[1][2] 以上 右下が a[4][4] 未満 の区間和
p s[4][4] - s[1][4] - s[4][2] + s[1][2]
# > 29
今回のまとめ
- 一次元配列では累積和を求めておくと、区間和は引き算1回で求めることが出来る。
- 二次元配列では累積和、区間和を求めるときに重複する区間に注意する。





