こんにちは!じゃいごテックのあつしです。
今回は尺取り法というアルゴリズムをご紹介します。
尺取り法とは
数列から取り出す範囲の先頭と末尾のインデックス情報を記憶して、先頭・末尾の位置をスライドさせた分の変化量を加減算して範囲内の総数を計算する方法です。
区間の最大値や条件を満たす区間を求める時によく使うアルゴリズムです。
サンプルコード
n 個の要素を持つ配列 ary の連続する k 個の要素の最大合計値を求めるコードです。
# しゃくとり法
# 左端と右端をずらして加減算を行っていく
def func1(n, k, ary)
# 最大区間 max_total と total を最初の区間合計で初期化
max_total = total = ary[0..k - 1].sum
# 次の区間以降をループ処理
1.upto(n - k) do |index|
# ary[index - 1] は計算区間から外れるので total から引く
total = total - ary[index - 1]
# ary[index + k - 1] は計算区間に追加されるので total に足す
total = total + ary[index + k - 1]
# total が max_total を超えていたら更新する
if total > max_total
max_total = total
end
end
max_total
end
# sumメソッドで計算を行う(2重ループ)
def func2(n, k, ary)
# max_total を最初の区間合計で初期化
max_total = ary[0..k - 1].sum
# 次の区間以降をループ処理
1.upto(n - k).each do |index|
# ary[index] から k 個分の要素の合計を計算し total へ代入
total = ary[index..index + k - 1].sum
# total が max_total を超えていたら更新する
if total > max_total
max_total = total
end
end
max_total
end
# ******************************
# n 個の要素を持つ配列 ary があり
# 連続する k 個の合計最大値を求める
# ******************************
# 計算条件
n = 10000
k = 5000
a = 100
# ランダムを固定
srand(0)
# ランダム配列生成
ary = Array.new(n) { rand(a) }
# 問題確認用
#p ary
puts "n = #{n}, k = #{k}"
puts "--------"
# func1: 尺取り法で処理
# 計算量 = k + (n - k) * 3
start = Time.now
puts func1(n, k, ary)
puts <<~"EOS"
尺取り法
処理時間: #{Time.now - start}
計算量: #{k + (n - k) * 3}
EOS
puts "--------"
# func2: sumメソッドで処理
# 計算量 = k + (n - k) * (k + 1)
start = Time.now
puts func2(n, k, ary)
puts <<~"EOS"
sumメソッド
処理時間: #{Time.now - start}
計算量: #{k + (n - k) * (k + 1)}
EOS
サンプルコードの計算量と実行時間
尺取り法では n の桁と計算量の桁が同じペースで増えますが、sumメソッド(2重ループ)では n の桁が1個増えると計算量の桁が2個増えます。
処理時間で見ると、 10の8乗後半から2秒程度の処理時間がかかるようになり、 paiza.IO でタイムオーバーが出始めました。
尺取り法の計算量
| func1 尺取り法 | 計算量 k + (n - k) * 3 | 実行時間 |
| n = 10, k = 5 | 2 * 101 | 0.0000727 |
| n = 50, k = 25 | 1 * 102 | 0.0000717 |
| n = 100, k = 50 | 2 * 102 | 0.0000740 |
| n = 500, k = 250 | 1 * 103 | 0.0000928 |
| n = 1000, k = 500 | 2 * 103 | 0.0001254 |
| n = 5000, k = 2500 | 1 * 104 | 0.0003154 |
| n = 10000, k = 5000 | 2 * 104 | 0.0005538 |
| n = 50000, k = 25000 | 1 * 105 | 0.0026233 |
| n = 100000, k = 50000 | 2 * 105 | 0.0052483 |
sumメソッド(2重ループ)の計算量
| func2 sumメソッド | 計算量 k + (n - k) * (k + 1) | 実行時間 |
| n = 10, k = 5 | 4 * 101 | 0.0000288 |
| n = 50, k = 25 | 7 * 102 | 0.0000384 |
| n = 100, k = 50 | 3 * 103 | 0.0000636 |
| n = 500, k = 250 | 6 * 104 | 0.0002440 |
| n = 1000, k = 500 | 3 * 105 | 0.0006390 |
| n = 5000, k = 2500 | 6 * 106 | 0.0136840 |
| n = 10000, k = 5000 | 3 * 107 | 0.0542430 |
| n = 50000, k = 25000 | 6 * 108 | 1.1968878 |
| n = 100000, k = 50000 | 3 * 109 | 4.8570418 |
サンプルコードの動作確認
paiza.IO で要素数 n 、 計算範囲 k を変えて実行してみることが出来ます。
サンプルコードの処理解説
サンプルコードを以下の条件で実行した時の処理を解説します。
条件
- n = 10
- k = 5
- 0 <= 各要素の値 < 10
- ary = [5, 0, 3, 3, 7, 9, 3, 5, 2, 4]
1. 最初の区間(インデックス 0 から 4)までを足して max_total, total を初期化する
- [5, 0, 3, 3, 7].sum -> 5 + 0 + 3 + 3 + 7 = 18
- max_total = 18, total = 18
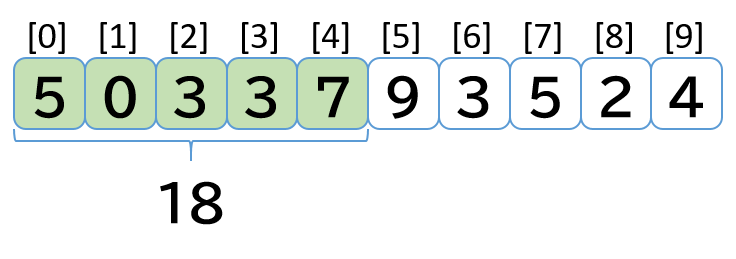
index を 1 から 10 - 5 = 5 までカウントアップしてループ処理を行う
2. index = 1 の処理
- [5, 0, 3, 3, 7] 先頭の 5 を外すので 18 - 5 = 13 を total に代入する
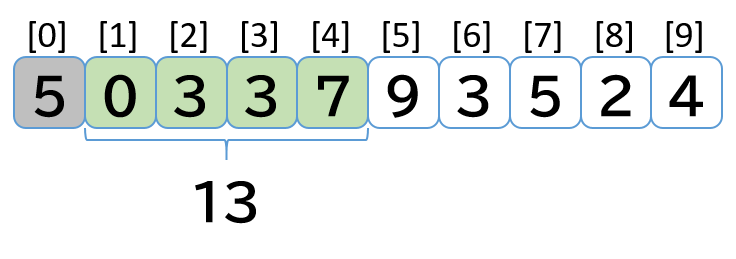
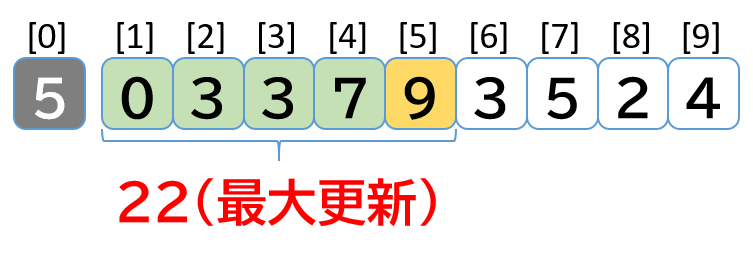
- [0, 3, 3, 7] 末尾に 9 を追加するので 13 + 9 = 22 を total に代入する
- max_total = 18 < total = 22 なので max_total = 22 で更新する
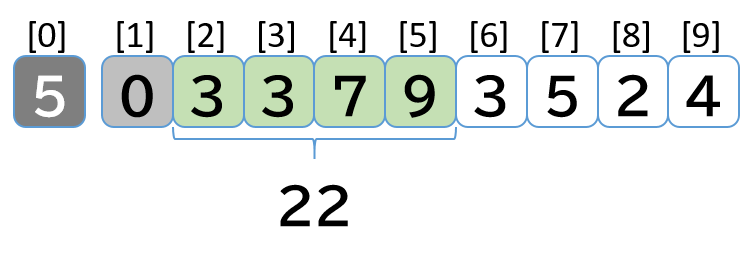
3. index = 2 の処理
- [0, 3, 3, 7, 9] 先頭の 0 を外すので 22 - 0 = 22 を total に代入する
- [3, 3, 7, 9] 末尾に 3 を追加するので 22 + 3 = 25 を total に代入する
- max_total = 22 < total = 25 なので max_total = 25 で更新する

4. index = 3 の処理
- [3, 3, 7, 9, 3] 先頭の 3 を外すので 25 - 3 = 22 を total に代入する
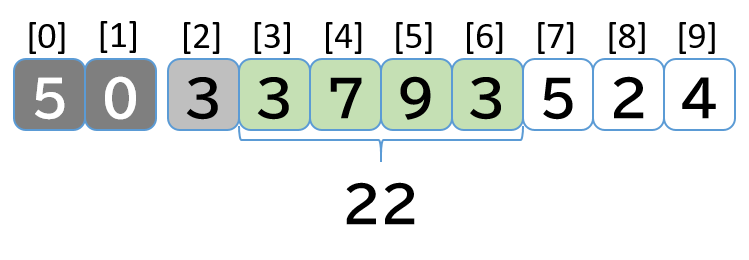
- [3, 7, 9, 3] 末尾に 5 を追加するので 22 + 5 = 27 を total に代入する
- max_total = 25 < total = 27 なので max_total = 27 で更新する

5. index = 4 の処理
- [3, 7, 9, 3, 5] 先頭の 3 を外すので 27 - 3 = 24 を total に代入する
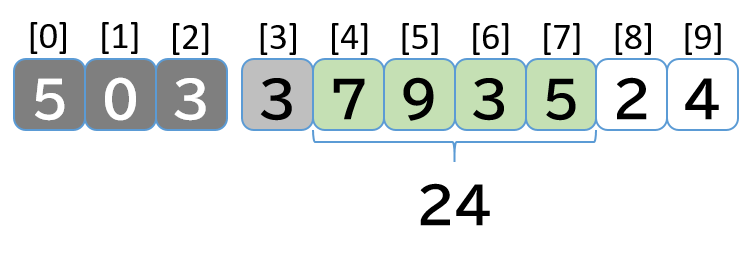
- [7, 9, 3, 5] 末尾に 2 を追加するので 24 + 2 = 26 を total に代入する
- max_total = 27 > total = 26 なのでなにもしない
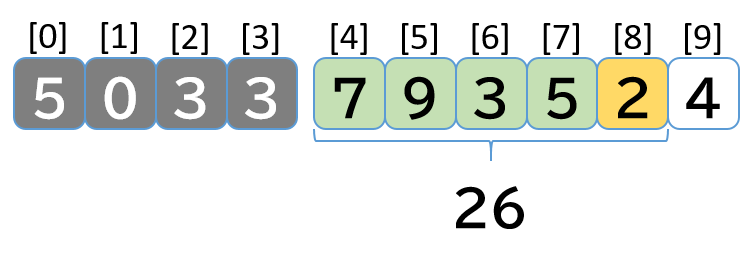
6. index = 5 の処理
- [7, 9, 3, 5, 2] 先頭の 7 を外すので 26 - 7 = 19 を total に代入する
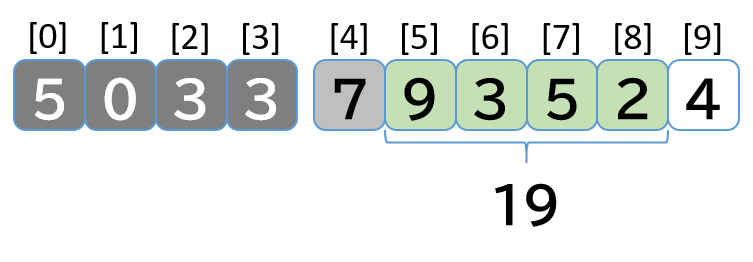
- [9, 3, 5, 2] 末尾に 4 を追加するので 19 + 4 = 23 を total に代入する
- max_total = 27 > total = 23 なのでなにもしない
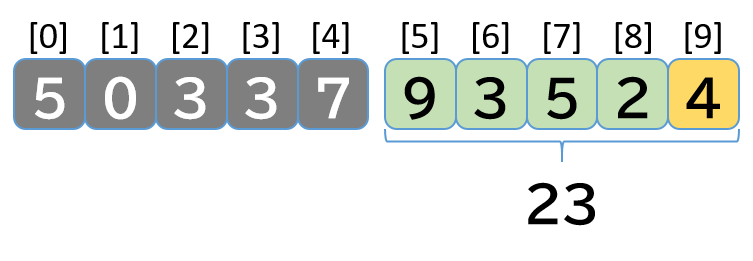
- max_total = 27 を答えとして出力する
今回のまとめ
尺取り法は始点・終点の位置を記憶しておき、始点・終点をスライドさせて値を加減算していく方法で、条件を満たす区間の長さや数を求めるのに適したアルゴリズムです。

尺取り法は理解しやすいアルゴリズムだと思うので是非使ってみて下さい。




