こんにちは!じゃいごテックのあつしです。
今回はpaiza DPメニュー 「セクション4【連続列】 STEP1, FINAL」 を解説します。
DPメニューは動的計画法(Dynamic Programming, DP)に関する6個のセクションで構成されています。
セクション4【連続列】は、隣り合う数列の値が昇順(または降順)に並んでいる区間のうち、最長であるものの長さを求める問題です。
STEP問題 を解いてみる
簡単な解説は付けていますが、難しいと感じたら下記の記事も参考にしてみて下さい。
分割統治法・動的計画法
メソッドの定義と呼び出し
標準入力・標準出力
STEP1: 最長増加連続部分列 (paizaランク B 相当)
n人分の身長の配列aが与えられ、隣り合う身長の値が昇順(前項の値以上)に並んでいる区間のうち、最長であるものの長さを求める問題です。
漸化式
dp[i] = 1
(初期値 = 1)dp[i] = dp[i - 1] + 1 (a[i -1] <= a[i])
(前項の値以上の時はカウントアップする)dp[i] = 1 (a[i -1] > a[i])
(前項の値未満の時は初期値 = 1に戻す)
解答例
INPUT1 = <<~"EOS"
5
160
178
170
190
190
EOS
OUTPUT1 = <<~"EOS"
3
EOS
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# dpテーブル初期化
dp = [1]
# dpテーブル更新
# 前項の値以上ならdpテーブルをカウントアップ
# そうでないならdpテーブルを 1 にもどす
1.upto(n - 1) do |i|
dp[i] = a[i - 1] <= a[i] ? dp[i - 1] + 1 : 1
end
# dpの最大値(最大区間数)を返す
dp.max
end
puts solve(STDIN.read)
# puts solve(INPUT1)
# > 3
整数n, 配列aを受け取る。dpに[1]を代入する。
(要素単体での最長は1)i = 1 ~ n-1で繰り返し処理を設定する。- dp[i] = a[i - 1] <= a[i] ? dp[i - 1] + 1 : 1
- 前項の値以上ならdpテーブルをカウントアップ
- そうでないならdpテーブルを 1 にもどす
- dp[i] = a[i - 1] <= a[i] ? dp[i - 1] + 1 : 1
- dpの最大値(最大区間数)を返す
入出力例1の処理
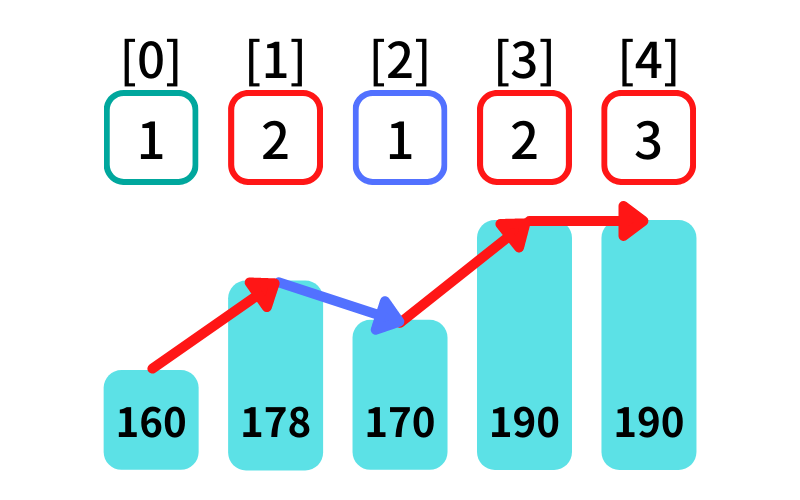
- dp[0] = 1 (初期化)
- dp[1] = 2 (160 ≦ 178 -> True)
- dp[2] = 1 (178 ≦ 170 -> False)
- dp[3] = 2 (170 ≦ 190 -> True)
- dp[4] = 3 (190 ≦ 190 -> True)
最大区間数 3 (dp[2]~dp[4])
FINAL問題: 最長減少連続部分列 (paizaランク B 相当)
※ paizaレベルアップ問題集 DPメニューより
問題
n 人が横一列に並んでいます。左から i 番目の人を人 i と呼ぶことにします。人 i の身長は a_i [cm]です。
人 l ,人 l+1, ... , 人 r からなる区間 [l, r] について、すべての l ≦ i < r に対して a_i ≧ a_{i+1} が成り立っているとき、区間 [l, r] は逆背の順であると呼ぶことにします。また、区間 [l, r] の長さを r-l+1 とします。
逆背の順であるような区間のうち、最長であるものの長さを出力してください。
入力される値
n
a_1
a_2
...
a_n
- 1行目に、横一列に並んでいる人の人数 n が与えられます。
- 続く n 行のうち i 行目では、人 i の身長 a_i が与えられます。
入力値最終行の末尾に改行が1つ入ります。
期待する出力
逆背の順であるような区間のうち、最長であるものの長さを出力してください。
また、末尾に改行を入れ、余計な文字、空行を含んではいけません。
条件
すべてのテストケースにおいて、以下の条件をみたします。
- 1 ≦ n ≦ 200,000
- 100 ≦ a_i ≦ 200
- 入力例1
- 5
187
192
115
108
109
- 出力例1
- 3
攻略ポイント
ポイント
- 漸化式を立てて問題を解く。
問題を解く流れ
入出力例をコピペしてヒアドキュメントで変数に代入し、データを確認します。正しく受け取れていれば確認用コードは削除します。
INPUT1 = <<~"EOS" 5 187 192 115 108 109 EOS OUTPUT1 = <<~"EOS" 3 EOS p INPUT1 # > "5\n187\n192\n115\n108\n109\n" p OUTPUT1 # > "3\n"
続いて、問題を解くsolveメソッドを変数の下に定義し、入力データを受け取る処理を書きます。
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# 確認用コード
[n, a]
end
# 確認用コード
p solve(INPUT1)
# > [5, [187, 192, 115, 108, 109]]
データが正しく受け取れていれば、solve メソッドに処理を追加していきます。
※ 不等号の向きが変わるだけで、STEP1と同じ問題です。
-
整数n, 配列aを受け取る。dpに[1]を代入する。
(要素単体での最長は1)i = 1 ~ n-1で繰り返し処理を設定する。- dp[i] = a[i - 1] >= a[i] ? dp[i - 1] + 1 : 1
- 前項の値以下ならdpテーブルをカウントアップ
- そうでないならdpテーブルを 1 にもどす
- dp[i] = a[i - 1] >= a[i] ? dp[i - 1] + 1 : 1
- dpの最大値(最大区間数)を返す
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# dpテーブル初期化
dp = [1]
# dpテーブル更新
# 前項の値以上ならdpテーブルをカウントアップ
# そうでないならdpテーブルを 1 にもどす
1.upto(n - 1) do |i|
dp[i] = a[i - 1] >= a[i] ? dp[i - 1] + 1 : 1
end
# 確認用コード
dp
end
# 確認用コード
p solve(INPUT1)
# > [1, 1, 2, 3, 1]
p solve(INPUT1) == OUTPUT1
# > false
dpテーブルの内容が良さそうなら、出力を整えれば完成です。
p solve(INPUT1) == OUTPUT1 -> true を確認するために、出力を文字列に変換して末尾に改行を加えます。
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# dpテーブル初期化
dp = [1]
# dpテーブル更新
# 前項の値以上ならdpテーブルをカウントアップ
# そうでないならdpテーブルを 1 にもどす
1.upto(n - 1) do |i|
dp[i] = a[i - 1] >= a[i] ? dp[i - 1] + 1 : 1
end
# dpの最大値(最大区間数)を文字列に変換し末尾に改行を追加
dp.max.to_s << "\n"
end
# 確認用コード
p solve(INPUT1)
# > "3\n"
p solve(INPUT1) == OUTPUT1
# > true
入出力例での動作確認が出来ましたので、標準入力からのデータ受け取りに変更して、手動で動作確認をしたら提出します。
複数行のデータ受け取りなので STDIN.read を使います。(入力終了は Ctrl+D 又は Ctrl+Z)
解答コード
def solve(input_lines)
# 入力受け取り
n, *a = input_lines.split("\n").map(&:to_i)
# dpテーブル初期化
dp = [1]
# dpテーブル更新
# 前項の値以上ならdpテーブルをカウントアップ
# そうでないならdpテーブルを 1 にもどす
1.upto(n - 1) do |i|
dp[i] = a[i - 1] >= a[i] ? dp[i - 1] + 1 : 1
end
# dpの最大値(最大区間数)を文字列に変換し末尾に改行を追加
dp.max.to_s << "\n"
end
puts solve(STDIN.read)
入出力例1の処理
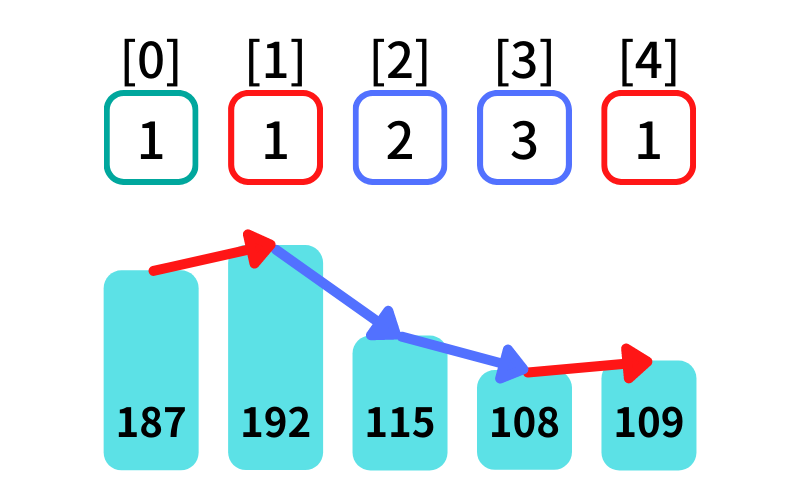
- dp[0] = 1 (初期化)
- dp[1] = 2 (187 ≧ 192 -> False)
- dp[2] = 1 (192 ≧ 115 -> True)
- dp[3] = 2 (115 ≧ 108 -> True)
- dp[4] = 3 (108 ≧ 109 -> False)
最大区間数 3 (dp[1]~dp[3])
今回のまとめ
セクション4は連続して増加(または減少)する区間の数を求める問題でした。

今回の問題はDPメニューのなかでも理解しやすい問題だったと思います。




