いもす法とは
いもす法は累積和を応用したアルゴリズムです。
区間の入口と出口で要素分の加算・減算を行って累積和を求めることで、任意の区間に要素がいくつ収まっているかを高速に計算することが出来ます。
いもす法の手順
文章だとイメージしづらいので、お店の来客数を例に考えてみたいと思います。
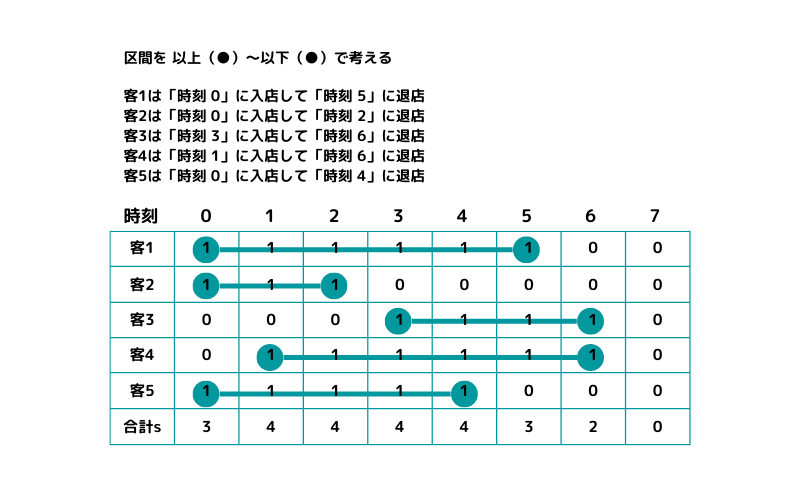
お客さんの入店時刻・退店時刻が与えられたときの、時刻ごとの客数を考えてみます。
お客さんの入店・退店時刻
- 客 1 は時刻 0 に入店して時刻 5 に退店する
- 客 2 は時刻 0 に入店して時刻 2 に退店する
- 客 3 は時刻 3 に入店して時刻 6 に退店する
- 客 4 は時刻 1 に入店して時刻 6 に退店する
- 客 5 は時刻 0 に入店して時刻 4 に退店する
下図のようになり、合計sが時刻ごとのお客さんの数となります。
いもす法を使わない計算方法 サンプルコード
いもす法を使わずに、二重ループで計算すると以下のようになります。
お客さんの人数を m とすると計算量 O(n*m)
n = 7
# 入退出時間の情報
el_times = [[0, 5],
[0, 2],
[3, 6],
[1, 6],
[0, 4]]
# 各時刻のお客さんの人数を計算する
s = Array.new(n, 0)
el_times.each do |enter, leave|
enter.upto(leave) do |time|
s[time] += 1
end
end
p s
# > [3, 4, 4, 4, 4, 3, 2]
半開区間で考えてみる
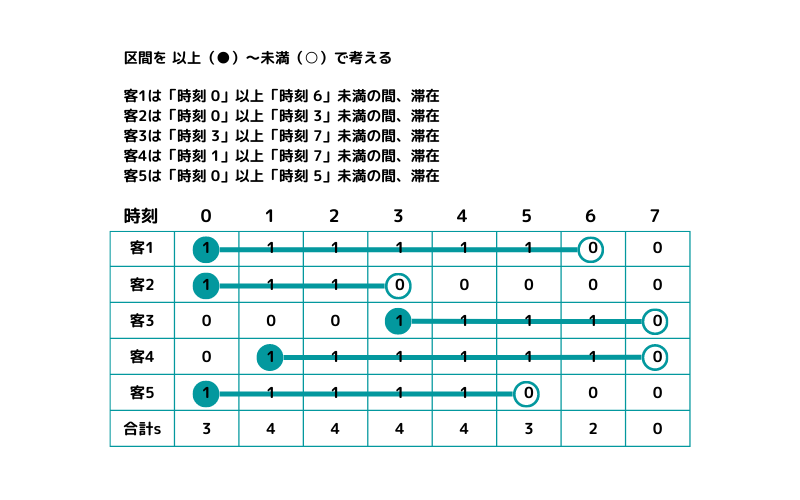
半開区間(以上~未満)で考えると次のようになります。
入店時刻で1増えて、退店時刻の次の時刻で1減っていることが分かります。
いもす法手順1 入口で加算、出口で減算する
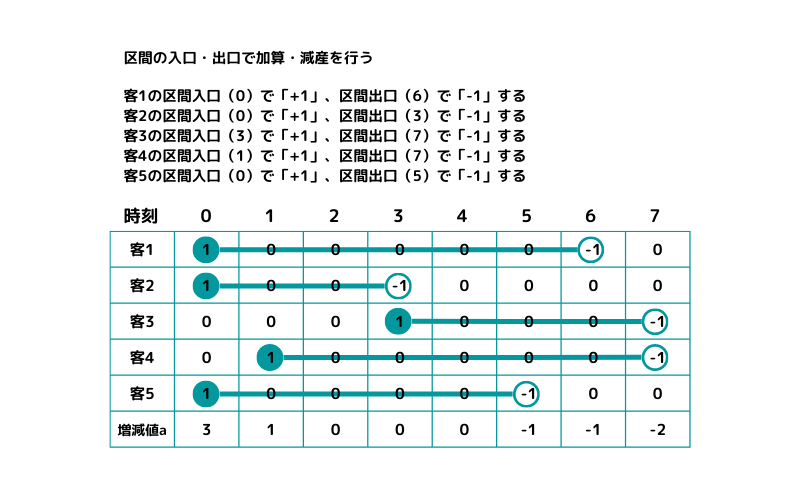
各お客さんの入店時刻で1増やして、退店時刻の次の時刻で1減らす表を作ってみます。
増減値 a が時刻ごとのお客さんの増減値(入店退店数)となります。お客さんの人数を m とすると計算量 O(m)
出入口で加減算する サンプルコード
n = 7
# 入退出時間の情報
el_times = [[0, 5],
[0, 2],
[3, 6],
[1, 6],
[0, 4]]
# 入退出時間の増減を計算する
a = Array.new(n + 1, 0)
el_times.each do |enter, leave|
a[enter] += 1
a[leave + 1] -= 1
end
p a
# > [3, 1, 0, 0, 0, -1, -1, -2]
いもす法手順2 加算減算した配列の累積和を計算する
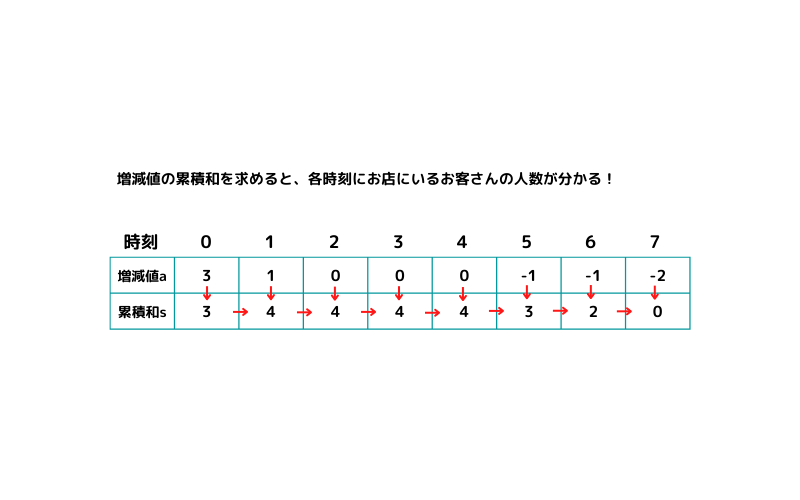
増減値が格納されている、配列a の累積和sを求めると、時刻ごとの客数が分かります。計算量 O(m)
増減値配列a の累積和を求める サンプルコード1
配列aの先頭要素を配列s[0]に格納してから、i をuptoメソッドで1からnまでループさせて計算しています。
サンプルコード1とサンプルコード2の計算イメージはこんな感じで、s[0]だけ他とは異なる処理をしています。
n = 7
# 入退出時間の情報
el_times = [[0, 5],
[0, 2],
[3, 6],
[1, 6],
[0, 4]]
# 入退出時間の増減を計算する
a = Array.new(n + 1, 0)
el_times.each do |enter, leave|
a[enter] += 1
a[leave + 1] -= 1
end
# 各時刻のお客さんの人数を計算する
s = Array.new(n + 1, 0)
s[0] = a[0]
1.upto(n) do |i|
s[i] = s[i - 1] + a[i]
end
p a
# > [3, 1, 0, 0, 0, -1, -1, -2]
p s
# > [3, 4, 4, 4, 4, 3, 2, 0]
増減値配列a の累積和を求める サンプルコード2
配列aの先頭要素を配列s[0]に格納してから、eachメソッドで2番目の要素から順に参照して計算しています。
n = 7
# 入退出時間の情報
el_times = [[0, 5],
[0, 2],
[3, 6],
[1, 6],
[0, 4]]
# 入退出時間の増減を計算する
a = Array.new(n + 1, 0)
el_times.each do |enter, leave|
a[enter] += 1
a[leave + 1] -= 1
end
# 各時刻のお客さんの人数を計算する
s = [a[0]]
a[1..].each do |f_val|
s << s[-1] + f_val
end
p a
# > [3, 1, 0, 0, 0, -1, -1, -2]
p s
# > [3, 4, 4, 4, 4, 3, 2, 0]
増減値配列a の累積和を求める サンプルコード3
累積和配列sを要素数n+1、初期値0で初期化してから、each_with_indexメソッドで配列aの先頭要素から順に要素の値f_valとインデックスiを一緒に参照し、s[i](前の時刻の累積和)+f_val(要素の値)を求めています。
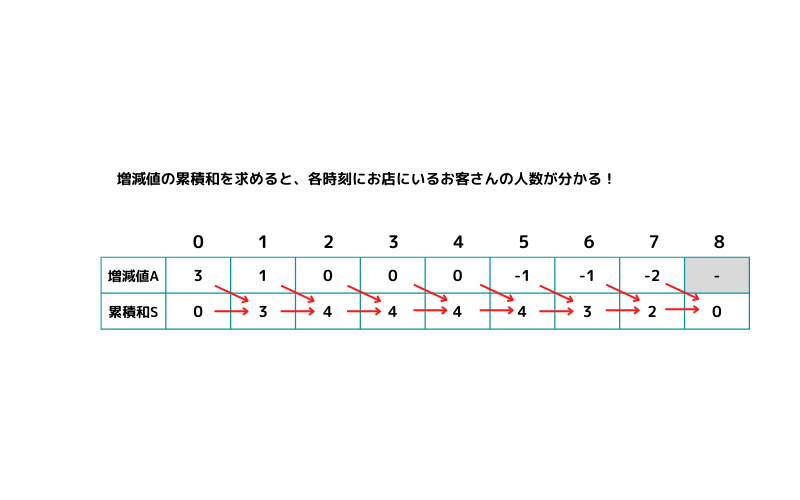
時刻0の前に空の区間0(開店前の客数=0)を用意する方法で、時刻tの人数を知りたい場合、累積和s[t + 1]を参照することになります。
サンプルコード3の計算イメージはこんな感じです。空の区間を追加するため要素数が1増えますが、すべての要素を同じ計算式で求めることが出来ます。
n = 7
# 入退出時間の情報
el_times = [[0, 5],
[0, 2],
[3, 6],
[1, 6],
[0, 4]]
# 入退出時間の増減を計算する
a = Array.new(n + 1, 0)
el_times.each do |enter, leave|
a[enter] += 1
a[leave + 1] -= 1
end
# 各時刻のお客さんの人数を計算する
s = Array.new(n + 1, 0)
a.each_with_index do |f_val, i|
s[i + 1] = s[i] + f_val
end
p a
# > [3, 1, 0, 0, 0, -1, -1, -2]
p s
# > [0, 3, 4, 4, 4, 4, 3, 2, 0]
これで各時刻ごとのお客さんの人数がすぐに求められるようになりました!
また、二重ループでの計算量は、O(n*m)でしたが、いもす法ではO(n+m)になりました!
二次元のいもす法
二次元配列でもいもす法を使うことが出来ます。
例として縦4×横4の二次元配列a上に、次の3つの矩形範囲(長方形)を重ねることを考えてみます。
左上がa[0][0]、右下がa[2][2]の矩形範囲
左上がa[1][1]、右下がa[3][3]の矩形範囲
左上がa[1][1]、右下がa[2][2]の矩形範囲
それぞれのイメージはこんな感じ。
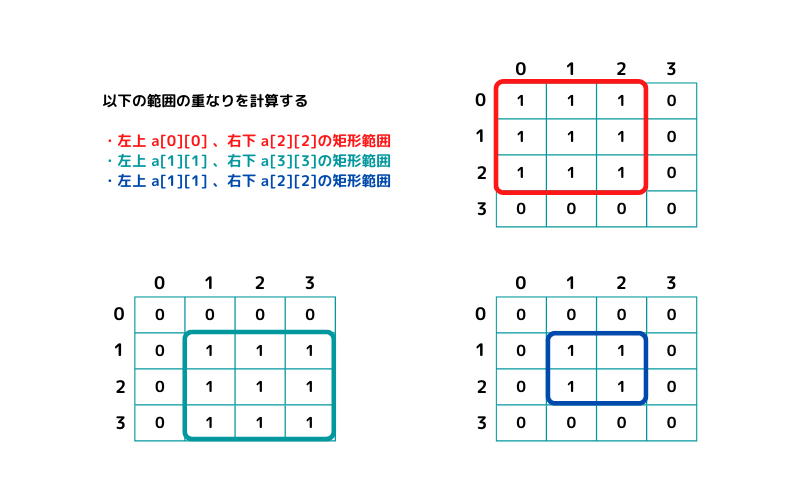
重ね合わせると、こんな感じですね。
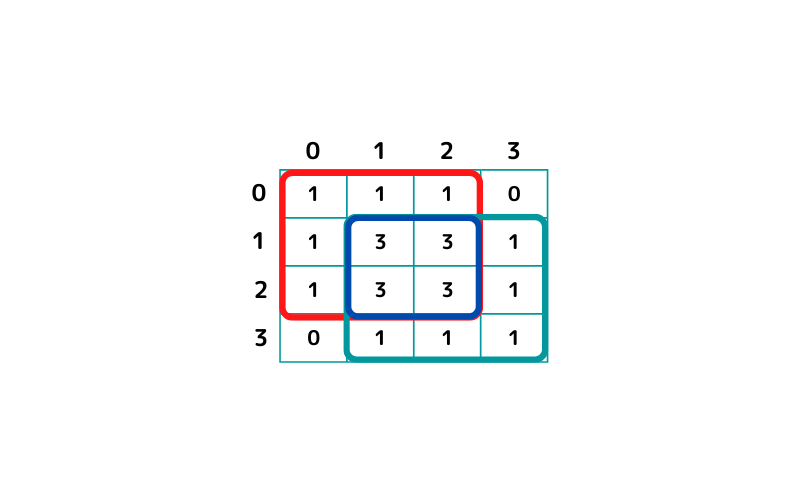
いもす法を使わない計算方法 サンプルコード
まずは、いもす法を使わない方法で計算してみます。長方形の数=n、縦=h、横=w とすると O(n*h*w)
h = 4
w = 4
r1 = [[0, 0], [2, 2]]
r2 = [[1, 1], [3, 3]]
r3 = [[1, 1], [2, 2]]
a = Array.new(h) { Array.new(w, 0) }
p a
# >[[0, 0, 0, 0],
# > [0, 0, 0, 0],
# > [0, 0, 0, 0],
# > [0, 0, 0, 0]]
[r1, r2, r3].each do |(sy, sx), (ey, ex)|
sy.upto(ey) do |y|
sx.upto(ex) do |x|
a[y][x] += 1
end
end
end
p a
# >[[1, 1, 1, 0],
# > [1, 3, 3, 1],
# > [1, 3, 3, 1],
# > [0, 1, 1, 1]]
個別の矩形範囲を確認してみる
まずは個別の矩形範囲について見てみましょう。
二次元配列も一次元配列のように、入口と出口で加算・減算を行います。二次元になっているので入口・出口は4か所になります。
左上がa[0][0]、右下がa[2][2]の矩形範囲はこんな感じ
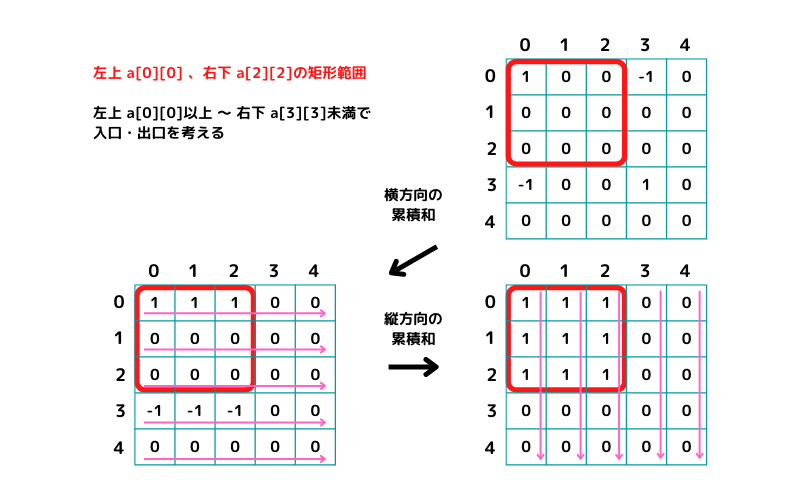
左上がa[0][0]、右下がa[2][2]範囲のサンプルコード
h = 4
w = 4
r1 = [[0, 0], [2, 2]]
a1 = Array.new(h + 1) { Array.new(w + 1, 0) }
s1 = Array.new(h + 1) { Array.new(w + 1, 0) }
(sy, sx), (ey, ex) = r1
# 入口・出口で加減算
a1[sy][sx] += 1
a1[sy][ex + 1] -= 1
a1[ey + 1][sx] -= 1
a1[ey + 1][ex + 1] += 1
p a1
# > [[ 1, 0, 0, -1, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [-1, 0, 0, 1, 0],
# > [ 0, 0, 0, 0, 0]]
# 横方向の累積和
0.upto(h) do |y|
0.upto(w) do |x|
s1[y][x] = a1[y][x]
s1[y][x] += s1[y][x - 1] if x > 0
end
end
p s1
# > [[ 1, 1, 1, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [-1, -1, -1, 0, 0],
# > [ 0, 0, 0, 0, 0]]
# 縦方向の累積和
1.upto(h) do |y|
0.upto(w) do |x|
s1[y][x] += s1[y - 1][x]
end
end
p s1
# > [[ 1, 1, 1, 0, 0],
# > [ 1, 1, 1, 0, 0],
# > [ 1, 1, 1, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0]]
左上がa[1][1]、右下がa[3][3]の矩形範囲はこんな感じ
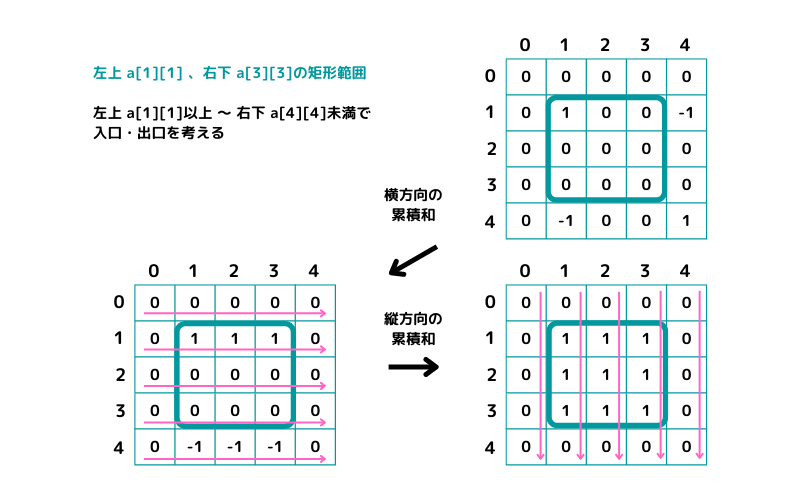
左上がa[1][1]、右下がa[3][3]範囲のサンプルコード
h = 4
w = 4
r2 = [[1, 1], [3, 3]]
a2 = Array.new(h + 1) { Array.new(w + 1, 0) }
s2 = Array.new(h + 1) { Array.new(w + 1, 0) }
(sy, sx), (ey, ex) = r2
# 入口・出口で加減算
a2[sy][sx] += 1
a2[sy][ex + 1] -= 1
a2[ey + 1][sx] -= 1
a2[ey + 1][ex + 1] += 1
p a2
# > [[ 0, 0, 0, 0, 0],
# > [ 0, 1, 0, 0, -1],
# > [ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, -1, 0, 0, 1]]
# 横方向の累積和
0.upto(h) do |y|
0.upto(w) do |x|
s2[y][x] = a2[y][x]
s2[y][x] += s2[y][x - 1] if x > 0
end
end
p s2
# > [[ 0, 0, 0, 0, 0],
# > [ 0, 1, 1, 1, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, -1, -1, -1, 0]]
# 縦方向の累積和
1.upto(h) do |y|
0.upto(w) do |x|
s2[y][x] += s2[y - 1][x]
end
end
p s2
# > [[ 0, 0, 0, 0, 0],
# > [ 0, 1, 1, 1, 0],
# > [ 0, 1, 1, 1, 0],
# > [ 0, 1, 1, 1, 0],
# > [ 0, 0, 0, 0, 0]]
左上がa[1][1]、右下がa[2][2]の矩形範囲はこんな感じ
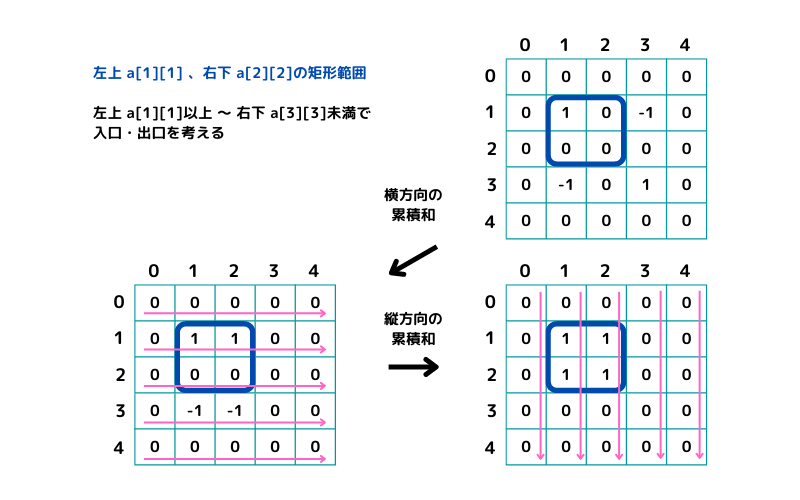
左上がa[1][1]、右下がa[2][2]範囲のサンプルコード
h = 4
w = 4
r3 = [[1, 1], [2, 2]]
a3 = Array.new(h + 1) { Array.new(w + 1, 0) }
s3 = Array.new(h + 1) { Array.new(w + 1, 0) }
(sy, sx), (ey, ex) = r3
# 入口・出口で加減算
a3[sy][sx] += 1
a3[sy][ex + 1] -= 1
a3[ey + 1][sx] -= 1
a3[ey + 1][ex + 1] += 1
p a3
# > [[ 0, 0, 0, 0, 0],
# > [ 0, 1, 0, -1, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, -1, 0, 1, 0],
# > [ 0, 0, 0, 0, 0]]
# 横方向の累積和
0.upto(h) do |y|
0.upto(w) do |x|
s3[y][x] = a3[y][x]
s3[y][x] += s3[y][x - 1] if x > 0
end
end
p s3
# > [[ 0, 0, 0, 0, 0],
# > [ 0, 1, 1, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, -1, -1, 0, 0],
# > [ 0, 0, 0, 0, 0]]
# 縦方向の累積和
1.upto(h) do |y|
0.upto(w) do |x|
s3[y][x] += s3[y - 1][x]
end
end
p s3
# > [[ 0, 0, 0, 0, 0],
# > [ 0, 1, 1, 0, 0],
# > [ 0, 1, 1, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0]]
全ての範囲をまとめて計算してみる
それでは全ての矩形範囲をまとめて処理してみましょう。矩形の数=n、縦=h、横=w とすると O(n+h*w)
イメージはこんな感じです。
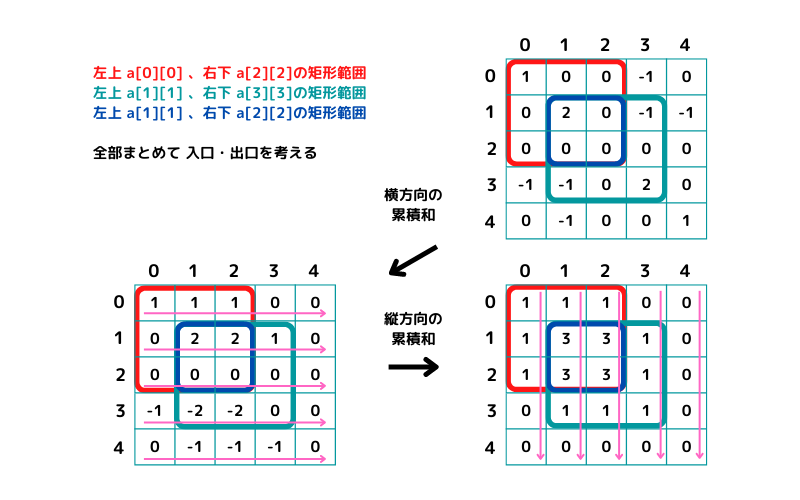
二次元のいもす サンプルコード1
まずは、矩形範囲を個別に確認した時と同じコードです。
h = 4
w = 4
r1 = [[0, 0], [2, 2]]
r2 = [[1, 1], [3, 3]]
r3 = [[1, 1], [2, 2]]
a = Array.new(h + 1) { Array.new(w + 1, 0) }
s = Array.new(h + 1) { Array.new(w + 1, 0) }
# 入口・出口で加減算
[r1, r2, r3].each do |(sy, sx), (ey, ex)|
a[sy][sx] += 1
a[sy][ex + 1] -= 1
a[ey + 1][sx] -= 1
a[ey + 1][ex + 1] += 1
end
p a
# > [[ 1, 0, 0, -1, 0],
# > [ 0, 2, 0, -1, -1],
# > [ 0, 0, 0, 0, 0],
# > [-1, -1, 0, 2, 0],
# > [ 0, -1, 0, 0, 1]]
# 横方向の累積和
0.upto(h) do |y|
0.upto(w) do |x|
s[y][x] = a[y][x]
s[y][x] += s[y][x - 1] if x > 0
end
end
p s
# > [[ 1, 1, 1, 0, 0],
# > [ 0, 2, 2, 1, 0],
# > [ 0, 0, 0, 0, 0],
# > [-1, -2, -2, 0, 0],
# > [ 0, -1, -1, -1, 0]]
# 縦方向の累積和
1.upto(h) do |y|
0.upto(w) do |x|
s[y][x] += s[y - 1][x]
end
end
p s
# > [[ 1, 1, 1, 0, 0],
# > [ 1, 3, 3, 1, 0],
# > [ 1, 3, 3, 1, 0],
# > [ 0, 1, 1, 1, 0],
# > [ 0, 0, 0, 0, 0]]
二次元のいもす サンプルコード2
次は、横の累積和と縦の累積和を1回の二重ループにまとめたコードです。
二次元配列範囲外の参照を防ぐために、条件分岐で処理を切り替えています。
h = 4
w = 4
r1 = [[0, 0], [2, 2]]
r2 = [[1, 1], [3, 3]]
r3 = [[1, 1], [2, 2]]
a = Array.new(h + 1) { Array.new(w + 1, 0) }
s = Array.new(h + 1) { Array.new(w + 1, 0) }
# 入口・出口で加減算
[r1, r2, r3].each do |(sy, sx), (ey, ex)|
a[sy][sx] += 1
a[sy][ex + 1] -= 1
a[ey + 1][sx] -= 1
a[ey + 1][ex + 1] += 1
end
p a
# > [[ 1, 0, 0, -1, 0],
# > [ 0, 2, 0, -1, -1],
# > [ 0, 0, 0, 0, 0],
# > [-1, -1, 0, 2, 0],
# > [ 0, -1, 0, 0, 1]]
# 累積和
0.upto(h) do |y|
0.upto(w) do |x|
s[y][x] = a[y][x]
s[y][x] += s[y - 1][x] if y > 0
s[y][x] += s[y][x - 1] if x > 0
s[y][x] -= s[y - 1][x - 1] if y > 0 && x > 0
end
end
p s
# > [[ 1, 1, 1, 0, 0],
# > [ 1, 3, 3, 1, 0],
# > [ 1, 3, 3, 1, 0],
# > [ 0, 1, 1, 1, 0],
# > [ 0, 0, 0, 0, 0]]
二次元のいもす サンプルコード3
y方向、x方向の最初の要素の前に空の区間を追加することで、範囲外の参照を防いでいます。
一次元のときと同様、縦と横の要素数が1増えますが、ループ内で累積和を求める計算式は全て同じになります。
h = 4
w = 4
r1 = [[0, 0], [2, 2]]
r2 = [[1, 1], [3, 3]]
r3 = [[1, 1], [2, 2]]
a = Array.new(h + 1) { Array.new(w + 1, 0) }
s = Array.new(h + 2) { Array.new(w + 2, 0) }
# p a
# >[[ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0],
# > [ 0, 0, 0, 0, 0]]
# 入口・出口で加減算
[r1, r2, r3].each do |(sy, sx), (ey, ex)|
a[sy][sx] += 1
a[sy][ex + 1] -= 1
a[ey + 1][sx] -= 1
a[ey + 1][ex + 1] += 1
end
p a
# > [[ 1, 0, 0, -1, 0],
# > [ 0, 2, 0, -1, -1],
# > [ 0, 0, 0, 0, 0],
# > [-1, -1, 0, 2, 0],
# > [ 0, -1, 0, 0, 1]]
# 累積和
0.upto(h) do |y|
0.upto(w) do |x|
s[y + 1][x + 1] = a[y][x] + s[y][x + 1] + s[y + 1][x] - s[y][x]
end
end
p s
# > [[ 0, 0, 0, 0, 0, 0],
# > [ 0, 1, 1, 1, 0, 0],
# > [ 0, 1, 3, 3, 1, 0],
# > [ 0, 1, 3, 3, 1, 0],
# > [ 0, 0, 1, 1, 1, 0],
# > [ 0, 0, 0, 0, 0, 0]]
今回のまとめ
- いもす法は区間の入口・出口で加算・減算したあと、累積和を求める。
- 一次元配列、二次元(多次元)配列で使うことが出来る。
- 一次元配列で要素の数=N、配列の長さ=Lとすると
- 二重ループで計算すると O(N*L)
- いもす法で計算すると O(N+L)
- 二次元配列で範囲の数=N、縦=H、横=Wとすると、
- 三重ループで計算すると O(N*H*W)
- いもす法で計算すると O(N+H*W)

paizaでは累積和の練習メニュー・応用メニューにいもす法の問題も用意されていますので、ぜひ挑戦してみて下さい!!




